Deep white matter analysis (DeepWMA): fast and consistent tractography segmentation

Abstract

White matter tract segmentation, i.e. identifying tractography fibers (streamline trajectories) belonging to anatomically meaningful fiber tracts, is an essential step to enable tract quantification and visualization. In this study, we present a deep learning tractography segmentation method (DeepWMA) that allows fast and consistent identification of 54 major deep white matter fiber tracts from the whole brain. We create a large-scale training tractography dataset of 1 million labeled fiber samples, and we propose a novel 2D multi-channel feature descriptor (FiberMap) that encodes spatial coordinates of points along each fiber. We learn a convolutional neural network (CNN) fiber classification model based on FiberMap and obtain a high fiber classification accuracy of 90.99% on the training tractography data with ground truth fiber labels. Then, the method is evaluated on a test dataset of 597 diffusion MRI scans from six independently acquired populations across genders, the lifespan (1 day - 82 years), and different health conditions (healthy control, neuropsychiatric disorders, and brain tumor patients). We perform comparisons with two state-of-the-art tract segmentation methods. Experimental results show that our method obtains a highly consistent tract segmentation result, where on average over 99% of the fiber tracts are successfully identified across all subjects under study, most importantly, including neonates and patients with space-occupying brain tumors. We also demonstrate good generalization of the method to tractography data from multiple different fiber tracking methods. The proposed method leverages deep learning techniques and provides a fast and efficient tool for brain white matter segmentation in large diffusion MRI tractography datasets.

1. Introduction

Diffusion magnetic resonance imaging (dMRI) allows mapping of white matter fiber tracts in the brain via a process called tractography (Basser et al., 2000). Tractography estimates fiber trajectories by following their probable tract orientations, enabling the measurement of microstructural white matter properties of fiber pathways (Basser et al., 2000; Mori and van Zijl, 2002; Westin et al., 2002). Tractography has been widely used for understanding neurological development, brain function, and brain disease, as described in several reviews (Ciccarelli et al., 2008; Yamada et al., 2009; Pannek et al., 2014; Piper et al., 2014; Essayed et al., 2017). However, performing whole brain tractography on one individual subject can generate hundreds of thousands of fibers, which are not immediately useful to clinicians or researchers. Therefore, white matter tract segmentation, i.e. identifying tractography fibers (streamline trajectories) belonging to anatomically meaningful fiber tracts, is an essential step to enable tract quantification and visualization.

Automated and robust white matter segmentation can enable the analysis of new, large dMRI datasets that are being acquired to study complex neural systems across the lifespan and across brain disorders (Alexander et al., 2017; Thompson et al., 2017; Casey et al., 2018; Harms et al., 2018; Cetin-Karayumak et al., 2019). One category of automated white matter tract segmentation methods uses prior information in the form of an atlas, where tract segmentation is performed according to fiber terminations in cortical and subcortical structures (Sporns et al., 2005; Bullmore and Sporns, 2009; Gong et al., 2009; Zalesky et al., 2012; Bastiani et al., 2012; Ingalhalikar et al., 2014; Yeh et al., 2016; Bassett and Bullmore, 2017; Wassermann et al., 2016; Yeh et al., 2019). Another category of tract segmentation methods apply fiber clustering to segment white matter fibers based on their fiber trajectory (Ding et al., 2003; O’Donnell and Westin, 2007; Wassermann et al., 2010; Visser et al., 2011; Guevara et al., 2012; Jin et al., 2014; Prasad et al., 2014; Kumar et al., 2017; Garyfallidis et al., 2018; Siless et al., 2018).

Recent studies have applied deep learning techniques to perform automated white matter tract segmentation (refer to (Poulin et al., 2019) for a review). These deep learning tract segmentation techniques can be divided into voxel-based strategies and fiber-based strategies based on the input data provided to the network. The voxel-based strategies perform tract segmentation based on a predicted “tract presence” volume, where each voxel encodes the presence and/or orientation of a fiber tract. This strategy has enabled tract segmentation by fiber tracking following the predicted fiber directions (Reisert et al., 2018; Wasserthal et al., 2018, 2019). In contrast, the fiber-based strategies first perform tractography and then segment tractography fibers by classifying them into anatomical tracts using a convolutional neural network (CNN) or its extension (e.g., a graph CNN as applied in (Liu et al., 2019)) trained on fiber feature descriptors (Lam et al., 2018; Gupta et al., 2017a; Xu et al., 2019; Gupta et al., 2017b, 2018; Liu et al., 2019). Previously proposed fiber feature descriptors include curvature, torsion and distances to anatomical landmarks (Lam et al., 2018), as well as spatial coordinates of fiber points (Gupta et al., 2017a; Xu et al., 2019; Gupta et al., 2017b, 2018; Liu et al., 2019).

Deep learning tract segmentation methods have achieved good performance, but challenges still remain, particularly in consistent tract segmentation of dMRI data from different sources (e.g. across different acquisitions, healthy and disease populations, and different ages). Consistent tract segmentation is important in brain white matter analysis, required, e.g., for across-lifespan and multi-site studies that are currently underway in many large datasets (Alexander et al., 2017; Thompson et al., 2017; Casey et al., 2018; Harms et al., 2018; Cetin-Karayumak et al., 2019). The tract presence volume predicted by voxel-based methods provides a normalized and condensed representation of the raw dMRI data and thus can be robust to different acquisitions with different numbers of gradient directions, b-values and other parameters (Wasserthal et al., 2018, 2019). However, voxel-based methods could be challenged by local anatomical differences from subjects with high anatomical variability. For instance, prediction of a tract presence volume can be challenged by space-occupying lesions that displace fiber tracts, or by neuroanatomical changes during neurodevelopment. Fiber-based strategies using traditional machine learning approaches (e.g. fiber clustering techniques) can handle this large across-subject anatomical variability. For example, successful and consistent tract segmentation has been demonstrated in subjects across the lifespan and across different acquisition protocols (Zhang et al., 2018c), and in patients with brain tumors (Zhang et al., 2018c; Tunç et al., 2015; Garyfallidis et al., 2018; O’Donnell et al., 2017). However, such traditional methods usually require multiple time-consuming processing steps.

In this study, we propose a fiber-based deep learning method for fast and consistent white matter tract segmentation, which we refer to as the Deep White Matter Analysis (DeepWMA) method. We believe the proposed method is the first fiber-based deep learning tract segmentation method that can generalize to dMRI data across healthy and disease populations, across the lifespan, and across multiple dMRI acquisitions, as well as across multiple tractography methods. This investigation extends our initial conference publication (Zhang et al., 2019a) to 1) investigate the effect of different sizes of FiberMap, 2) provide detailed tract spatial overlap analysis, and 3) demonstrate successful tract segmentation on 3 additional populations, to include subjects across the full lifespan.

This paper has three main contributions. First, we create a large-scale training dataset of a million labeled tractography fibers from 100 healthy adult subjects, including fibers from anatomical fiber tracts and those from false positive tracking. Second, we propose a novel 2D multi-channel fiber feature descriptor (FiberMap) that is insensitive to the order of points along fibers and is robust to local anatomical differences. Third, we demonstrate successful tract segmentation on a large test dataset including a total of 597 subjects from 6 independently acquired populations.

2. Methods

Figure 1 gives an overview of the proposed DeepWMA method, including: (a) creation of the training tractography data (Section 2.1), (b) extraction of FiberMap fiber feature descriptor (Section 2.2), (c) training of the CNN fiber classification model (Section 2.3), and (d) prediction of the subject-specific tract segmentation (Section 2.4).

Figure 1:

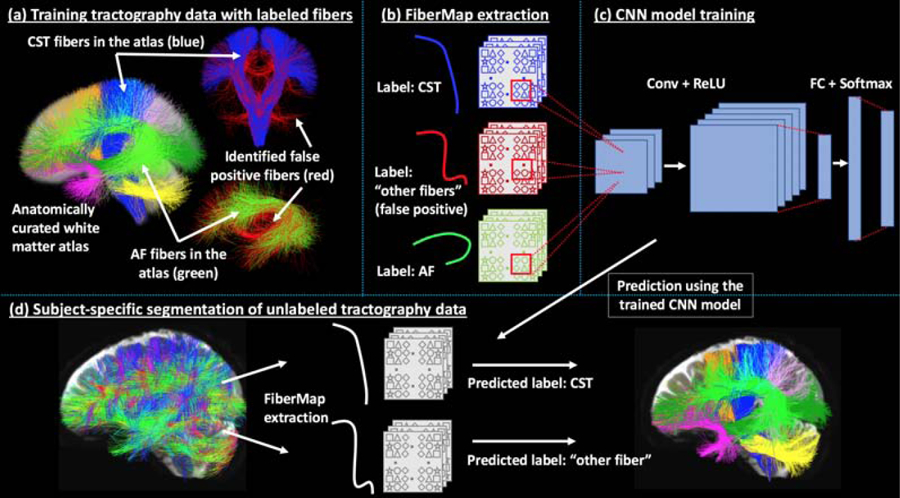
Method overview. A training tractography dataset (a) is created, where each fiber is associated with an anatomical tract label (e.g. AF or CST) or a category of “other fibers,” including false positive fibers (shown in red). A 2D multi-channel feature descriptor (FiberMap) (b) is extracted for each fiber. A CNN tract classification model (c) (see Section 2.3 for the detailed CNN architecture) is trained based on the FiberMap descriptors. Subject-specific tract segmentation (d) is performed by FiberMap feature extraction for each fiber, followed by tract label prediction using the trained CNN model.

2.1. Datasets

In this study, we created a training tractography dataset including a total of 1 million fiber samples with anatomical labels (Section 2.1.1), which were used for CNN tract segmentation model training. The trained model was tested to segment tractography data of a total of 597 subjects from six independently acquired dMRI test datasets (Section 2.1.2) for experimental evaluation.

2.1.1. Training tractography data

A good training dataset for tractography segmentation should include fiber samples from not only true positive anatomical fiber tracts but also fiber samples from false positive tracking that is known to be dominant in tractography data (Maier-Hein et al., 2017). In our study, we created a large tractography training dataset including 1 million fiber samples. These training fiber samples were labeled into 55 tract categories consisting of 54 anatomical deep white matter fiber tracts and a tract category of “other fibers” including, most importantly, those from false positive tracking. Figure 1(a) gives a visualization of example training fiber samples.

To create the training tractography data, we leveraged the ORG-800FC-100HCP white matter tractography atlas (Zhang et al., 2018c), which is provided by the O’Donnell Research Group (ORG) at the Laboratory for Mathematics in Imaging and is now available online¹. This ORG atlas is an anatomically curated white matter atlas using population-based brain anatomical information and expert neuroanatomical knowledge (Zhang et al., 2018c). The atlas includes whole-brain tractography data (computed using a two-tensor unscented Kalman filter (UKF) (Malcolm et al., 2010) fiber tracking method) from 100 healthy Human Connectome Project (HCP) (Glasser et al., 2013) subjects. In the present study, we used the expert curated fibers in the ORG atlas from a total of 54 deep white matter tracts, such as the arcuate fasciculus (AF) and corticospinal tract (CST) (see Supplementary Table I for the list of the 54 tracts and the number of fiber samples in each anatomical tract category). A total of 273,379 training fiber samples in 54 anatomical tract categories were included. The remaining uncurated fibers in the ORG atlas were assigned the tract category of “other fibers.” We also computed fibers from false positive tracking and assigned these fibers the tract category of “other fibers.” This resulted in a total of 726,621 fiber samples in this category. We note that the ORG atlas was designed to perform tract segmentation in combination with a data-driven fiber clustering pipeline (a comparison method used in the present study, as introduced in Section 2.5.2) (Zhang et al., 2018c), where false positive fibers were identified and removed from the atlas in order to facilitate subject-specific false positive fiber removal when applying the atlas to tractography data from new subjects. Thus, false positive fibers were not included in the ORG atlas. We computed these fibers from the 100 atlas HCP subjects’ whole-brain UKF tractography by applying atlas-based clustering followed by outlier identification (Zhang et al., 2018c). Specifically, the tractography data of each HCP subject was clustered based on the ORG atlas using the whitematteranalysis (WMA)² fiber clustering package. Outlier subject-specific fibers that have improbable fiber trajectory were identified based on their fiber affinity to the atlas cluster (over 2 standard deviations from the cluster’s mean fiber affinity, as applied in (Zhang et al., 2018c). This data-driven outlier identification process has been successfully applied in multiple works from our group to identify false positive fibers (O’Donnell et al., 2017; Zhang et al., 2018b; Wu et al., 2018; Zhang et al., 2018a, 2019b, 2020b).

In total, in the curated training tractography data, there were a million fiber samples, where each fiber belonged to one of the 54 anatomical tract categories or the “other fibers” category. We note that the fiber samples in the training tractography data were randomly sampled from the whole-brain tractography data from 100 HCP subjects used for the ORG atlas generation. The proportion of fiber samples in each category thus represented the fiber proportions in the real brain tractography data. Such a sample distribution in the training data could be beneficial for robustly training a tract segmentation model. (Our unpublished results on curation of training data by including evenly distributed samples across all 55 tract categories, e.g., with data augmentation by repetition of fiber samples, showed unfavorable fiber classification performance).

2.1.2. Six independently acquired dMRI test datasets

For experimental evaluation, we used dMRI data from a total of 597 subjects from six independently acquired datasets with different diffusion imaging protocols. These testing subjects were across genders, across the lifespan (neonates, children, young adults and older adults, ranging in age from 1 day to 82 years), and across different health conditions (healthy control, neuropsychiatric disorders, and neurosurgical patients with brain tumors). Table 1 gives an overview of the demographics and the dMRI acquisitions of the test datasets under study. The dHCP, ABIDE, HCP, CNP, and PPMI datasets were from public imaging repositories (as described in Table 1). Imaging data from the BTP dataset was acquired at Brigham and Women’s Hospital. The usage of the data was approved by the Partners Healthcare Institutional Review Board, and informed consent was obtained from all participants prior to scanning. Data preprocessing was performed to exclude potential artifacts, e.g., from eddy current and head motion effects. (Details of the preprocessing steps for each test dataset under study are included in Supplementary Text I.A.)

Table 1:

Demographics and dMRI acquisition of the six independent datasets studied.

Dataset	N	Age	Gender	H/D	dMRI data
dHCP	40	1 to 27 d (6.30±7.47)	15 F 25 M	40 H	b=400/1000/2600 s/mm2; 300 directions; TE/TR=90/3800 ms; resolution=1.5 mm3
ABIDE	70	5 to 17 y (12.0±3.1)	6 F 64 M	49 AUT 21 H	b=1000s/mm2; 64 directions; TE/TR=78/5200 ms; resolution=3 mm3
HCP	100	22 to 35 y (29.0±3.5)	54 F 46 M	100 H	b=3000s/mm2; 108 directions; TE/TR=89/5520 ms; resolution=1.25 mm3
CNP	204	21 to 50 y (33.3±9.3)	112 F	41 DHD 49 BD 50 SZ 125 H	b=1000s/mm2; 64 directions; TE/TR=93/9000 ms; resolution=2 mm3
PPMI	144	51 to 82 y (63.7±7.3)	51 F 93 M	102 PD 42 H	b=1000 s/mm2; 64 directions; TE/TR=88/7600 ms; resolution=2 mm3
BTP	39	23 to 82 y (48.9±15.3)	16 F 23 M	39 BTP	b=2000 s/mm2; 31 directions; TE/TR=98/12700ms; resolution=2.3 mm3
Total number of subjects: N =597

Abbreviations: Dataset: dHCP - Developing Human Connectome Project (Makropoulos et al., 2018); ABIDE - Autism Brain Imaging Data Exchange (Di Martino et al., 2017); HCP - Human Connectome Project (Essen et al., 2013) (different subjects from the ones used in the training data); CNP - Consortium for Neuropsychiatric Phenomics (Poldrack et al., 2016); PPMI - Parkinson’s Progression Markers Initiative (Marek et al., 2011); BTP - Brain Tumor Patient. Age: d - day; y - year; Gender: F - female; M - male. Healthy/Disease (H/D): AUT - autism; ADHD - attention-deficit/hyperactivity disorder; BP - bipolar disorder; H - healthy; SZ - schizophrenia; PD - Parkinson’s disease; BTP - brain tumor patient.

2.1.3. Whole-brain tractography

We computed whole-brain tractography data per subject in each test dataset using the two-tensor UKF method³, which was the same fiber tracking method as used for generating the training data. We chose the two-tensor UKF method because it has been demonstrated to be highly robust for successful tract segmentation across the lifespan (Zhang et al., 2018c) and highly sensitive, especially in the presence of crossing fibers and peritumoral edema (Zhang et al., 2018c; Chen et al., 2015; Liao et al., 2017; Gong et al., 2018). For each of the subjects under study, there were about 1 million fibers in the whole-brain UKF tractography. In addition to the UKF method, we also applied two additional fiber tracking methods to evaluate our proposed method’s ability to generalize to tractography data computed from different methods. (Two additional fiber tracking methods include the diffusion tensor imaging (DTI) model (Basser et al., 2000) and the constrained spherical deconvolution (CSD) model (Tournier et al., 2010). See Section 2.5 for details of this experimental evaluation.) Visual and quantitative quality control of the tractography was performed using a quality control tool in the WMA software (Zhang et al., 2018c; O’Donnell and Westin, 2007). (Details of the tractography computation and parameters are included in Supplementary Text I.B.)

2.2. FiberMap tractography fiber feature descriptor

Our goal is to design a fiber representation, or feature descriptor, for effective classification of fibers belonging to different anatomical tracts. In tractography data, a fiber streamline is represented by a sequence of fiber points. The most straightforward fiber representation is to concatenate the spatial coordinates (x, y, z) of all fiber points into a sequential feature vector (x₁, y₁, z₁, …, x_n, y_n, z_n). However, such a representation provides limited performance for fiber classification due to the following issues. First, the sequential representation is sensitive to the order of points along the fibers. In tractography, fiber tracking provides no directional information. For example, a fiber in AF could be tracked either from Broca’s region in the frontal lobe to Wernicke’s region in the temporal lobe or from Wernicke’s region to Broca’s region. Using the sequential representation can be ineffective to classify fibers from the same tract but tracked from different directions. Second, the sequential representation concatenates the x-, y-, and z-coordinates of all fiber points together such that coordinates from different dimensions become neighbors (e.g., z₁ and x₂ are neighbors). This representation does not clearly depict the spatial neighborhood information between points along the fiber, which is important to properly capture the similarity of fibers with local anatomical differences. Beyond typical inter-subject anatomical variability, extreme anatomical variability due to space-occupying lesions that displace fiber tracts or neuroanatomical changes during neurodevelopment can result in large local anatomical differences within a tract. As a result, using the sequential representation can be ineffective to enable a tract segmentation method to generalize to data from different populations.

We propose to convert the sequential representation of fiber points resulting from tractography to a feature descriptor that is useful for fiber classification while addressing the above limitations. More specifically, the goal is to be able to correctly identify the corresponding training labeled fiber samples for a testing fiber regardless of the order of fiber points and potential local differences at certain fiber points. Conversion of sequential data to useful feature descriptors is an important problem in multiple domains, including classification of protein sequences (Kulmanov et al., 2017) and prediction of traffic speed (Ma et al., 2017). We propose a feature descriptor, FiberMap, which represents a fiber streamline as a 2D feature map with 3 channels. FiberMap is computed by flipping and repeating the spatial coordinates of points along the fiber (as described below). Unlike naive concatenation, FiberMap representation preserves the local structure of the data in the sense that neighboring x-, y-, and z-coordinates remain neighbors, while each x,y,z point is preserved in the 3 channels. The FiberMap descriptor is analogous to a 2D RGB (red, green, blue) image, which has 3 channels for each pixel. An important benefit of this image-like format is that it enables effective processing by CNNs, where additional fiber point spatial information can be accessed including not only neighboring points and other points along the fiber (see a toy example in Figure 2(a)). Flipping and repetition of existing data have been demonstrated to be effective in increasing the performance of CNNs, e.g., by increasing the diversity of data samples available for training CNN models in data augmentation (Wang and Perez, 2017). In the design of FiberMap, we leverage this strategy to create a fiber feature descriptor that enables a deeper network compared to the original sequential data format.

Figure 2:

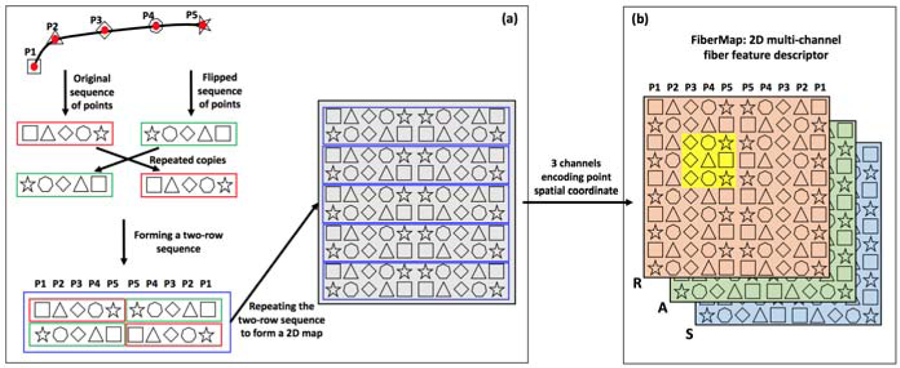
Illustration of the proposed FiberMap feature descriptor. (a) gives a step-by-step illustration of FiberMap computation by repeating and flipping the points along a fiber. (b) shows a graphic representation of FiberMap with 3 channels to encode the spatial Right-Anterior-Superior (RAS) coordinates of the fiber points, analogous to a 2D RGB image. An important benefit of FiberMap is that it enables effective processing by CNNs, where additional fiber point spatial information can be accessed including not only neighboring points and other points along the fiber (as illustrated in the yellow highlighted region).

A FiberMap is computed by repeating and flipping the coordinates of the points along a fiber as follows, as illustrated in Figure 2(a). For a fiber streamline, it is represented as a sequence of a fixed number of n_p points (i.e. P1 to P5, n_p=5 in this example; red rectangle). A flipped copy (green rectangle) is created by reversing the order of the points. This flipped copy is repeated twice, once to the right and once below, and the original sequence is repeated once below to the right. These steps result in a two-row sequence of points (blue rectangle), which is further repeated to generate a 2D map, i.e. the FiberMap descriptor. The repetition is performed n_r times (n_r=5 in this example), which results in a two-dimensional feature map (2n_r × 2n_p).

The FiberMap descriptor is a 2D multi-channel fiber descriptor, with 3 channels to encode the spatial Right-Anterior-Superior (RAS) coordinates of the fiber points, as illustrated in Figure 2(b). The size of the FiberMap descriptor is 2n_r ×2n_p ×3. In our experiments, we extract n_p=15 points per fiber, a reasonable number for fiber representation (Zhang et al., 2018c; O’Donnell and Westin, 2007), and for each point, its spatial Right-Anterior-Superior (RAS) coordinates are used to create the 3 channels. n_r is set to 15, which generated the highest fiber classification accuracy across multiple testing values. (See Supplementary Experiments 3.1 and 3.2 for details of the decision of hyperparameters n_r and n_p.) This produces a 30 × 30 × 3 dimensional FiberMap feature descriptor for each fiber, analogous to a 2D RGB image.

Due to this fiber representation, FiberMap provides an effective feature descriptor to handle the aforementioned limitations, as illustrated in Figure 3. First, FiberMap is relatively insensitive to the order of points along a fiber, as illustrated in (a and b). If the original sequence of points along the fiber in (a) is reversed to that in (b), the FiberMap descriptors of these two fibers are the same except for a difference of one row (the part that is the same between the two FiberMap descriptors is indicted using the red arrows). In addition, FiberMap is robust to local anatomical differences where certain fiber points can be different between fibers from the same anatomical structure, as illustrated in (b and c). The fiber in (c) is similar to that in (b), but with a local anatomical difference at point P2. Because the neighboring points of P2 on FiberMap (highlighted in yellow in (b) and (c)) are similar, the difference at P2 will have a small influence on the computation of fiber similarity. In addition to the above graphic illustration, FiberMaps computed from the AF fibers are visually similar in (d and e), even though there are apparent local anatomical differences at the region near the temporal lobe (the right part of the AF fibers) and the order of points along the two AF fibers is different (the top row of the FiberMap is different). The CST FiberMap in (f) is very different from the two AF FiberMaps in (d and e), which is apparently informative to differentiate these fibers.

Figure 3:

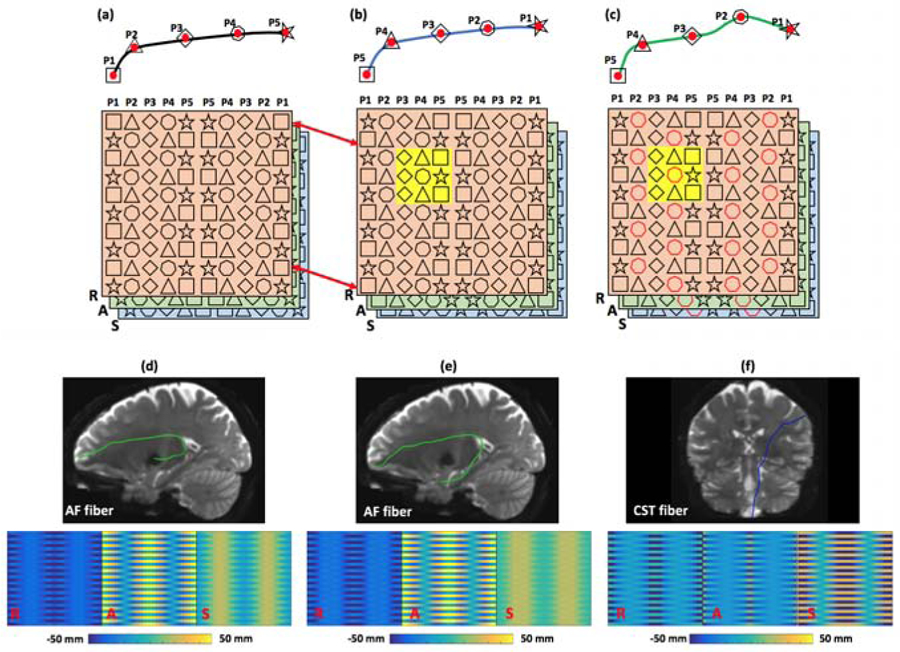
Illustration of insensitivity of FiberMap to the order of points along a fiber and robustness of FiberMap to local anatomical differences. (a) and (b) show an example of the insensitivity of FiberMap to the order of points along a fiber. (b) and (c) show an example of the robustness of FiberMap to local anatomical differences. (d), (e) and (f) give a visualization of FiberMaps computed from AF (d and e) and CST (f) fibers. For each FiberMap, the 3 channels are displayed separately, where the colorbar shows the R, A, S coordinate values (the same range between −50 mm and 50 mm is used for the three example fibers).

2.3. CNN tract segmentation model training

After extracting the FiberMap descriptor of each fiber in the training tractography data, we trained a CNN fiber classification model for tract segmentation. We used a traditional CNN architecture (Krizhevsky et al., 2012), which has been applied in previous fiber-based tract segmentation studies (Lam et al., 2018; Gupta et al., 2017b, 2018). We tested multiple kernel sizes and layers and here we present the most successful architecture (see Supplementary Figure 4 for a detailed network architecture diagram). This network contains eight convolutional layers (32, 32, 64, 64, 128, 128, 256 and 256 filters, respectively) with kernel size 3, where each convolutional layer is followed by a rectified linear units (ReLU) activation layer. A max pooling layer of size 2 and a dropout layer of 2.5 are used to prevent overfitting. The last convolutional layer is followed by three fully connected layers of size 128, 256 and 512, where each fully connected layer is followed by a dropout layer of 0.2. Then, a softmax layer is used with 55 outputs for the 54 anatomical tracts and the category of “other fibers.” Root Mean Square Propagation (RMSprop) is used for optimization with a loss function of categorical cross-entropy. The CNN is implemented using TensorFlow (version 1.12.0) (Abadi et al., 2016). In our experiments, we split the training dataset (a million labeled tractography fibers from 100 healthy adult subjects, classified into 55 tract categories), where 80% of the fibers were used for training and 20% for validation.

2.4. Tract segmentation of unlabeled tractography data

In this step, the trained CNN is applied to identify 54 anatomical tracts from whole-brain tractography data. First, subject-specific tractography is transferred to the atlas space so the coordinates of the fiber streamlines are in the same space as the training tractography data. This is done by performing an affine registration between the baseline (b=0) image of the subject (moving image) and the atlas population mean T2 image (reference image) using 3D Slicer⁴ (Fedorov et al., 2012). The obtained transform is then applied to the subject-specific tractography data. We note that because our method only needs a roughly aligned tractography data in the atlas space, a volume-based affine registration is sufficient, rather than a more complex deformable transformation or a tractography-based registration. Next, after FiberMap feature extraction is performed, all fibers are classified based on the trained CNN model into one of the 54 anatomical tract categories or the “other fibers” category (Figure 1(d)). Source code and the trained CNN model will be available online, via SlicerDMRI project (http://dmri.slicer.org).

2.5. Experimental evaluation

We performed four experiments. First, we tested the effect of the number of repetitions (n_r) when generating FiberMap to classify fibers belonging to different anatomical tracts. Second, we compared FiberMap to several existing fiber feature descriptors for fiber classification. Third, we compared the proposed DeepWMA method to two state-of-the-art tract segmentation methods. Fourth, we conducted an experiment to investigate the ability of DeepWMA to generalize to tractography data generated by several different fiber tracking methods.

2.5.1. Comparison of fiber feature descriptors using training tractography dataset

We assessed five feature descriptors that used RAS point coordinates and/or fiber curvature and torsion at points along a fiber. The 1D-RAS descriptor concatenates RAS coordinates into a 1D vector (size: 3n×1). The 2D-RAS descriptor concatenates RAS coordinates into a 2D vector (size: n×3) (Xu et al., 2019). The CurTor descriptor concatenates curvature and torsion (as implemented in TRAFIC⁵) (size: n × 2) (Lam et al., 2018). The 2D-RAS+CurTor descriptor concatenates the CurTor and 2D-RAS descriptors (size: n × 5) (Xu et al., 2019). The proposed FiberMap descriptor is described above (size: 2n ×2n ×3). Experimental comparison was performed on the training tractography dataset, where ground truth fiber labels were available. For consistency, n=15 points per fiber (Zhang et al., 2018c; O’Donnell and Westin, 2007) were used across all descriptors. For each descriptor, a CNN fiber classification model was trained and the parameters were well tuned. Specifically, for the 1D-RAS descriptor, we trained a 1D CNN containing one convolutional layer (32 filters) with kernel size 3, followed by a ReLU activation layer, a max pooling layer of size 2 and a dropout layer of 2.5. The last convolutional layer was followed by three fully connected layers of size 128, 256 and 512, and then a softmax layer with 55 outputs for the 54 anatomical tracts and the category of other fibers. For the 2D-RAS, CurTor and 2D-RAS+CurTor descriptors, we used the same CNN architecture, containing two convolutional layers of 32 filters with kernel size 3, followed by a ReLU activation layer, a max pooling layer of size 2, and a dropout layer of 2.5. The last convolutional layer was followed by three fully connected layers of size 128, 256 and 512, and then a softmax layer with 55 outputs for the 54 anatomical tracts and the category of “other fibers.” For FiberMap, the CNN architecture was introduced in Section 2.3. For all the compared methods, RMSprop is used for optimization with a loss function of categorical cross-entropy. The CNN is implemented using TensorFlow (version 1.12.0) (Abadi et al., 2016). The overall fiber classification accuracy (the percentage of fibers that were correctly classified into their ground truth tract category), as well as the mean recall and the mean precision across all tract categories, were compared across feature descriptors. The same training and validation splits of the training tractography dataset were used across all descriptors.

2.5.2. Comparison of state-of-the-art tract segmentation methods in independently acquired test datasets

We evaluated the proposed DeepWMA method with comparison to WMA (a fiber-based tract segmentation method) and TractSeg⁶ (a voxel-based tract segmentation method). Briefly, the WMA method leverages the ORG fiber clustering atlas to perform segmentation using spectral clustering (O’Donnell et al., 2017, 2012). (We note that the ORG atlas was also used for training DeepWMA.) The TractSeg method uses a trained CNN to predict a tract orientation map (TOM) that encodes the presence and orientation of a fiber tract (Wasserthal et al., 2018, 2019). Fiber tracking is then performed within the TOM. (Additional description of each method is provided in Supplementary Text I.C.) Parameters of each method were set to default values as suggested by the software. To control for differences in the list of tracts defined by each method, we focused the comparison on the 34 tracts commonly defined across all methods.

The goal of this experiment is to compare the segmented tracts from the three different methods on the test datasets without ground truth fiber labels, while considering that there are small differences of the anatomical definitions across the different methods. Theresore, we proposed the following quantitative and visual assessments.

Tract identification rate:

We computed the mean tract identification rate (percentage of successfully identified tracts) across all subjects in each dataset. A tract was considered to be successfully identified if there were at least 20 fibers in an individual subject (as in (Zhang et al., 2018c)). The tract identification rate has several advantages as an evaluation metric: it has been successfully used for tract segmentation evaluation (Zhang et al., 2018c), it captures the most basic information about a method’s success to identify a tract, and it is straightforward to apply across segmentation methods regardless of any small differences in the shape or location of tracts as defined by each method.

Population tract heatmap:

The population tract heatmap of an individual tract (e.g. AF) quantifies the percentage of subjects that have fibers present in each voxel. We computed these heatmaps for each method and test dataset. The affine transform (as introduced in Section 2.4) was used to align each subject’s tract into the same space (the ORG atlas). We chose the affine transform because it was applicable to all subjects including neonates and brain tumor patients. The heatmaps were used for visualization of method performance and for assessing spatial overlap across methods.

Population tract spatial overlap:

To assess if fiber tracts obtained from different methods were spatially comparable, we compared the population tract heatmaps using the weighted Dice (wDice) coefficient. wDice is a metric designed specifically for measuring tract spatial overlap (Cousineau et al., 2017; Zhang et al., 2019b). It extends the standard Dice coefficient to non-binary maps and gives higher weighting to voxels with higher values. We note that the creation of the ORG atlas and the TractSeg training data both used White Matter Query Language (WMQL) (Wassermann et al., 2016) to perform initial fiber tract selection, followed by further tract refinement. Therefore, the segmented tracts using TractSeg, WMA and DeepWMA reflect the tract definitions from the same source. In the original study proposing TractSeg, WMA and TractSeg are compared in terms of tract spatial overlap (Wasserthal et al., 2018).

Subject-specific tract visualization:

To provide example subject-specific results, we rendered selected tract segmentation results from each method.

Computational time:

To assess the typical run time of each method, we performed an experiment using a Linux workstation equipped with both CPU and GPU. For simplicity, dMRI data from one HCP subject was used in this experiment. We measured run time using only a CPU (4 cores) and using the 4-core CPU plus one GPU. (For WMA, we only measured using the CPU because it does not use the GPU.)

2.5.3. Generalization to tractography data from different fiber tracking methods

In addition to the UKF tractography method used in the previous experiments, we tested the ability of DeepWMA to segment two additional types of tractography data: a traditional DTI streamline method (Basser et al., 2000) (implemented in SlicerDMRI⁷ (Norton et al., 2017; Zhang et al., 2020a)) and an advanced CSD-based tractography method (Tournier et al., 2010) (implemented in MRtrix⁸). (Details of whole-brain tractography are included in Supplementary Text I.B.) These three tractography methods are based on different fiber tracking models and are known to generate tractography data that varies quite significantly. For example, the DTI tractography is less sensitive in tracking through crossing fiber regions than the UKF and CSD methods, and the CSD method performs probabilistic tractography while the UKF and DTI methods perform deterministic tractography. DeepWMA was then applied to segment the whole-brain DTI and CSD tractography. Performance was assessed using the tract identification rate and population tract heatmaps. For comparison, we also performed tract segmentation on the DTI-based and CSD-based tractography using the WMA method and reported the tract identification rate.

3. Experimental results

3.1. Comparison of fiber feature descriptors

As shown in Table 2, the 1D-RAS and CurTor descriptors had low fiber classification accuracies (around 50%), while the 2D-RAS and 2D-RAS+CurTor descriptors obtained higher accuracies (around 87%). The FiberMap descriptor obtained the highest accuracy (about 91%), as well as the highest mean recall and precision values.

Table 2:

Comparison across different fiber feature descriptors on the training tractography data where ground truth fiber labels are available. For each feature descriptor, the overall fiber classification accuracy, i.e., the percentage of fibers that were correctly classified into their ground truth tract category in the validation split of the tractography data, is reported. In addition, the mean and the standard deviation of recall and those of precision across all tract categories are reported.

Feature descriptor	Accuracy	Recall	Precision
1D-RAS	47.26%	22.54 ± 15.46%	1.70 ± 0.92%
2D-RAS	88.03%	75.57 ± 10.80%	87.53 ± 4.99%
CurTor	48.98%	34.16 ± 17.67%	1.70 ± 0.63%
2D-RAS+CurTor	87.08%	75.22 ± 10.65%	86.38 ± 7.38%
FiberMap	90.99%	85.67 ± 5.72%	88.47 ± 5.19%

3.2. Comparison of state-of-the-art tract segmentation methods

Tract identification rate (Table 3):

Table 3:

Mean tract identification rate across the 34 tracts that were commonly defined across the three compared tract segmentation methods

Dataset	TractSeg	WMA	DeepWMA
dHCP	68.16% ± 18.68%	99.12% ± 2.03%	99.41% ± 1.85%
ABIDE	99.75% ± 1.02%	99.92% ± 0.34%	99.96% ± 0.24%
HCP	100.0% ± 0.00%	100.0% ± 0.00%	100.0% ± 0.00%
CNP	98.87% ± 3.16%	99.35% ± 1.77%	99.66% ± 0.61%
PPMI	99.29% ± 0.85%	99.76% ± 0.59%	99.74% ± 0.70%
BTP	94.42% ± 6.00%	98.27% ± 2.34%	99.17% ± 1.86%

For the ABIDE, HCP, CNP and PPMI datasets, all three methods performed well, where over 98.8% of the tracts could be successfully identified. For the dHCP and BTP datasets, the WMA and DeepWMA methods could identify over 98% of the tracts, while the TractSeg method identified only 68.18% of the tracts in dHCP and 94.42% of the tracts in BTP. (A Supplementary Figure 5 is provided to show the tract identification rate of each of the 34 tracts for each tract segmentation method.)

Population tract heatmap visualization (Figure 4):

Figure 4:

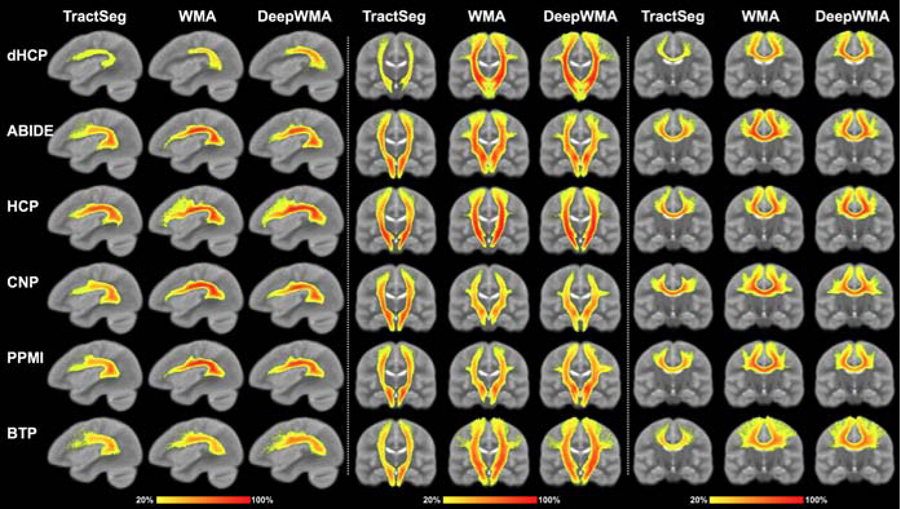
Visual comparison of the voxel-based population tract heatmaps of three example tracts (AF, CST and CC4, respectively) obtained using TractSeg, WMA and DeepWMA. The value of a voxel in the heatmaps represents the percentage of subjects that have fibers passing through the voxel (see colorbar). The background image is the ORG atlas population mean T2 image.

In general, the visual assessment demonstrated that the identified tracts were visually comparable across the three tract segmentation methods. However, we can observe that in most of the tracts, the WMA and DeepWMA methods generated more consistent tract segmentations across the population than the TractSeg method, in terms of a visually higher value in the heatmaps. For example, the heatmaps of corpus callosum 4 (CC4) from the WMA and DeepWMA methods (Figure 4) have more red voxels with a value over 90%. On the other hand, the TractSeg method had more consistent segmentation performance on several tracts. For example, the heatmap from the TractSeg method (Fig 4) has more yellow voxels with a value of 20% in the anterior part of the AF tract in dHCP.

Subject-specific tract visualization (Figure 5):

Figure 5:

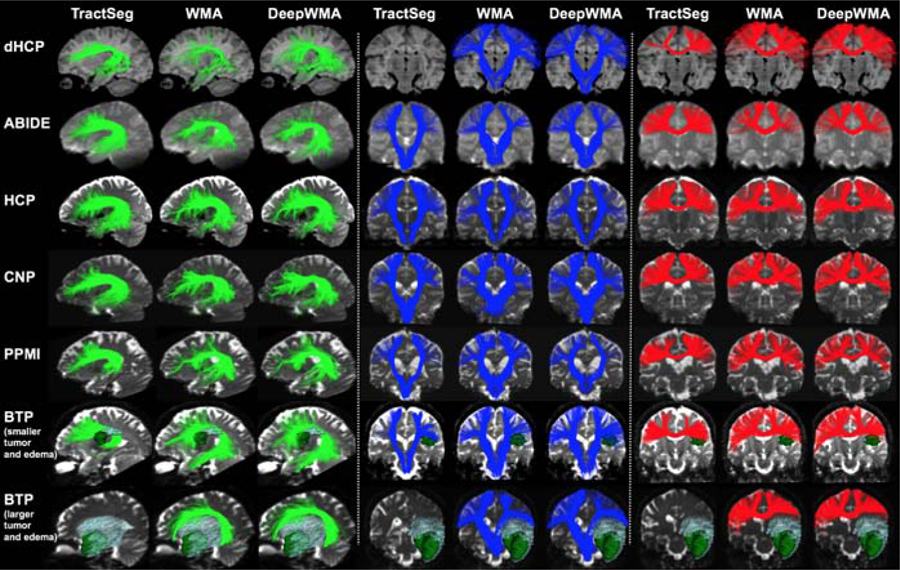
Visual comparison of three example subject-specific tracts (AF, CST and CC4, respectively) obtained using TractSeg, WMA and DeepWMA. Subjects in dHCP to PPMI datasets (top 5 rows) were selected as representative because their mean tract identification rate (across all tracts and methods) was closest to the population mean. In the BTP dataset (bottom 2 rows), two patients were selected as representative, where one patient had smaller tumor and edema and the other had relatively larger tumor and edema.

Visual assessment of subject-specific tracts demonstrated good performance of all methods in the example subjects from ABIDE, HCP, CNP and PPMI, as well as the brain tumor patient with smaller tumor and edema. However, unlike the fiber-based WMA and DeepWMA approaches, the voxel-based TractSeg method did not detect the AF, CST and CC4 tracts in the patient with larger tumor and edema and did not detect the CST tract in the neonate in the dHCP dataset.

Additional tract visualizations:

To show the performance of the proposed method on segmenting all tracts defined in the training data, a Supplementary Figure 6 is provided to show all 54 tracts obtained for an example HCP subject using DeepWMA. In addition, to demonstrate the performance of DeepWMA in dHCP and BTP (where DeepWMA and TractSeg had the most different results in terms of tract identification rate), we provide a visualization of segmented tracts from all subjects per dataset in Supplementary Figures 7 and 8 (the left AF tract is selected for illustration). Furthermore, to assess the anatomical validity of the segmented fiber tracts, we also provide a visualization of the brain regions through which the fiber tracts pass in Supplementary Figure 9 (the CST tract is selected for illustration).

Spatial tract overlap (Table 4):

Table 4:

Spatial overlap agreements (wDice) between each pair of the compared methods (TractSeg, WMA and DeepWMA). For each pair of the methods, we computed and reported the mean wDice across the 34 tracts that were commonly defined across all three methods.

Dataset	DeepWMA vs TractSeg	DeepWMA vs WMA	TractSeg vs WMA
dHCP	0.67 ± 0.11	0.91 ± 0.08	0.70 ± 0.11
ABIDE	0.80 ± 0.08	0.94 ± 0.02	0.79 ± 0.08
HCP	0.83 ± 0.07	0.96 ± 0.02	0.83 ± 0.07
CNP	0.83 ± 0.09	0.97 ± 0.02	0.82 ± 0.09
PPMI	0.82 ± 0.09	0.97 ± 0.01	0.82 ± 0.09
BTP	0.76 ± 0.10	0.93 ± 0.03	0.78 ± 0.09

The wDice overlap score of DeepWMA and WMA was high (over 0.91) across all test datasets under study. The wDice overlap of DeepWMA and TractSeg was also relatively high, particularly on the HCP and CNP datasets (wDice=0.83), even though these two methods used different training data. These results suggest that our method had good spatial coverage relative to the compared methods.

Computational time (Table 5):

Table 5:

Computational time of the TractSeg, WMA and DeepWMA methods on dMRI data from one HCP subject. We measured run time using only a CPU (4 cores) and using the 4-core CPU plus one GPU. (For WMA, we only measured using the CPU because it does not use the GPU.)

	Whole brain tractography	TOM prediction (TractSeg) or fiber classification (WMA/DeepWMA)	Fiber tracking for specific tracts
TractSeg	Not applicable	10 min (CPU), or 10 min (CPU+GPU)	27 min (CPU), or 22 min (CPU+GPU)
WMA	4 hours (CPU)	1.5 hours (CPU)	Not applicable
DeepWMA	4 hours (CPU)	41 min (CPU), or 8 min (CPU+GPU)	Not applicable Not applicable

For segmentation with WMA and DeepWMA, whole-brain UKF tractography containing about a million fibers was computed in data from one example HCP subject, which took about 4 hours using 4 CPU cores. To segment this whole-brain tractography, the CPU-based WMA method took about 1.5 hours using a CPU with 4 cores. The DeepWMA method required a shorter time of 41 minutes on the same 4-core CPU, or 8 minutes using the 4-core CPU plus 1 GPU (where the most time-consuming part includes input/output of the tractography data and the computation of FiberMap using the CPU). The TractSeg method required 37 minutes (CPU only) or 32 minutes (4-core CPU plus 1 GPU). This included approximately 10 minutes for prediction of TOMs and 25 minutes for fiber tracking (a total of 2,000 fibers per tract according to default settings for a total of 144,000 fibers) within the predicted TOMs.

3.3. Generalization to tractography data from different fiber tracking methods

Tract identification rate (Table 6):

Table 6:

Mean tract identification rate (across the 54 tracts identified using the baseline WMA method and the proposed DeepWMA) for the three fiber tracking methods.

Dataset	DTI		CSD		UKF
	WMA	DeepWMA	WMA	DeepWMA	WMA	DeepWMA
dHCP	77.98% ± 30.63%	74.11% ± 33.39%	88.63% ± 28.37%	88.97% ± 3.86%	99.41% ± 1.68%	99.60% ± 1.49%
ABIDE	78.16% ± 30.78%	77.12% ± 35.50%	99.53% ± 0.35%	99.92% ± 0.42%	99.87% ± 0.71%	99.97% ± 0.19%
HCP	95.55% ± 17.40%	93.54% ± 17.79%	99.74% ± 0.18%	99.32% ± 0.23%	99.93% ± 0.38%	100.0% ± 0.00%
CNP	82.59% ± 26.96%	81.98% ± 27.70%	99.30% ± 2.19%	98.42% ± 5.93%	99.61% ± 1.24%	99.66% ± 0.67%
PPMI	84.80% ± 24.07%	84.66% ± 24.43%	99.98% ± 0.10%	99.75% ± 0.94%	99.83% ± 0.48%	99.85% ± 0.56%
BTP	75.36% ± 25.07%	76.37% ± 28.10%	99.34% ± 1.62%	97.62% ± 4.96%	98.28% ± 2.69%	99.17% ± 2.72%

Overall, the WMA and DeepWMA methods obtained highly similar tract identification rates for each fiber tracking method and each dataset. For the traditional DTI fiber tracking method that was relatively insensitive in tracking through crossing fiber regions, over 74% of the tracts could be successfully detected across all test datasets under study. In particular, when using the DTI fiber tracking method in the HCP dataset, over 93% of the tracts were identified. For the CSD method that was a more advanced and sensitive fiber tracking method, over 98% of the fiber tracts were identified in all test datasets except the dHCP dataset, where about 89% of the tracts were identified. For the UKF method, over 99% of the tracts could be successfully identified in all test datasets under study, representing the highest tract identification rate across the three fiber tracking methods. This was most likely due to the fact that the UKF method was used for generating the training tractography data. (Supplementary Figure 10 shows the tract identification rate of each of the 54 tracts for each fiber tracking method.)

Population-wise heatmap (Figure 6) and subject-specific (Figure 7) tract visualizations:

Figure 6:

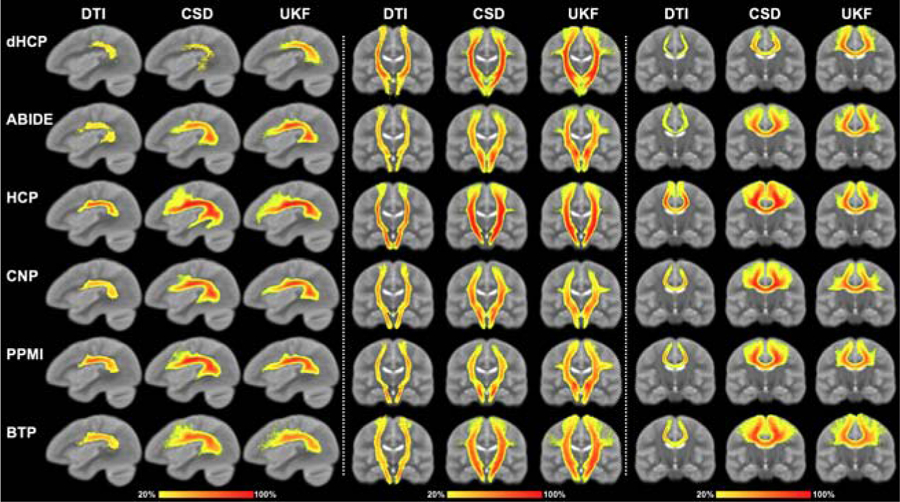
Voxel-based population tract heatmaps of three example tracts (AF, CST and CC4, respectively) obtained by applying DeepWMA on tractography data computed using the DTI, CSD and UKF fiber tracking methods. The value of each voxel in the heatmaps represents the percentage of subjects that have fibers passing through the voxel (see colorbar). The background image is the ORG atlas population mean T2 image.

Figure 7:

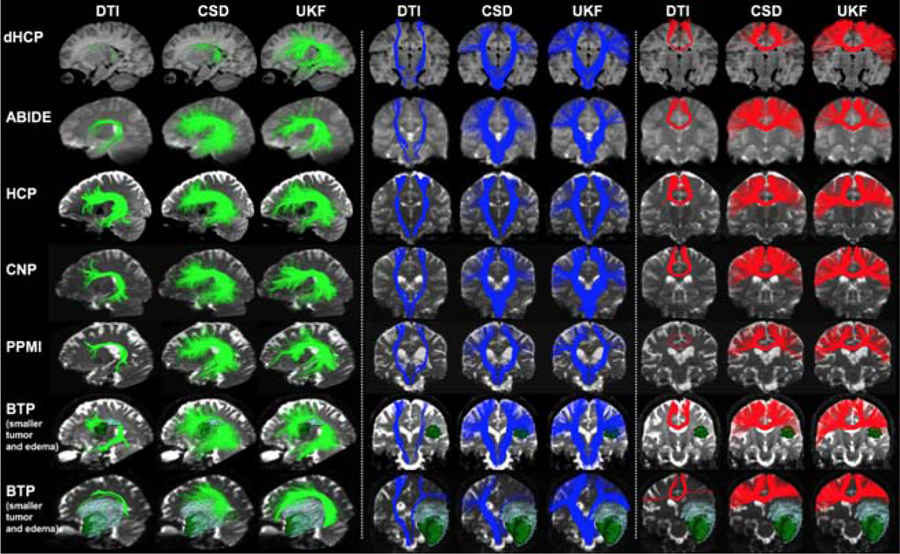
Subject-specific tract visualization of three example tracts (AF, CST and CC4, respectively) obtained by applying DeepWMA on tractography computed using the DTI, CSD and UKF methods. The same subjects as shown in Figure 5 are selected for visualization.

In general, across the fiber tracking methods, the example segmented fiber tracts were visually reasonable and comparable, even though the tractography data varied quite significantly across the three fiber tracking models. For example, the DTI method was insensitive in tracking through crossing fiber regions and thus it could hardly track the fibers connecting to the hand and face motor cortical regions in the CST and CC4 tracts, while the CSD and UKF methods managed to track these fibers.

4. Discussion

In this work, we proposed the first fiber-based deep learning method, DeepWMA, that allowed consistent tract segmentation across multiple dMRI acquisitions and across different populations including neonates and patients with space-occupying brain tumors. A summary of the experimental results includes the following points. First, we demonstrated highly consistent tract segmentation performance of DeepWMA on a large test dataset of 597 dMRI scans from six independently acquired populations. On average, over 99% of the fiber tracts were successfully identified across all subjects under study. Second, we showed that DeepWMA provided a good ability to generalize to tractography data from multiple different fiber tracking methods. For the high-quality HCP dataset, over 93% of fiber tracts were successfully identified across the three tested fiber tracking methods (UKF, CSD and DTI). Third, DeepWMA provided a fast and efficient tool for tract segmentation in large dMRI tractography datasets. While achieving similar results to WMA in terms of tract identification rate, tract visualization and spatial tract overlap, DeepWMA performed much faster by leveraging GPU computation (1.5 hours versus 8 minutes). Below, we discuss several detailed observations about the experimental results.

We demonstrated that the proposed FiberMap feature descriptor improved tract segmentation performance compared to several other descriptors. The different performance of these descriptors may relate to the following observations. In the 1D-RAS descriptor, the R, A and S coordinates from all points of a fiber were concatenated into a 1D vector, which could not clearly depict the spatial neighborhood information between points along the fiber and thus generated a feature descriptor that was not suitable for CNNs. The 2D-RAS descriptor preserved the neighborhood spatial relationship of the R, A and S coordinates and achieved the second best performance across all compared descriptors under study. The proposed FiberMap feature outperformed the 2D-RAS descriptor by including multiple flipped and repeated copies of the 2D-RAS descriptor and arranging these copies in an informative way. Flipping and repetition of existing data have been demonstrated to be effective in increasing the performance of CNNs, e.g., by increasing the diversity of data samples available for training CNN models in data augmentation (Wang and Perez, 2017). The CurTor descriptor was not successful, possibly because fibers from different tracts (e.g. different corpus callosum tracts) could have highly similar curvature and torsion values, causing the CurTor descriptor to be less discriminative, in line with the finding in (Xu et al., 2019). In addition, the different performance of these descriptors may relate to the different CNN architectures applied for each descriptor. The 1D-RAS descriptor could be used in combination with 1D CNN but not a 2D CNN as the other compared descriptors. The proposed FiberMap enables the application of 2D CNN with a deep network architecture with more convolution layers.

We performed an inspection of the fibers misclassified by DeepWMA in the training tractography data. By visual checking, we found that most fibers were at the boundary between the annotated anatomical fibers and the false positive fibers. Such fibers are difficult, even impossible, to be definitively delineated in tractography because of a lack of ground truth. Therefore, we believe that the obtained 90.99% fiber classification accuracy on the training tractography data represents a good tractography segmentation performance. An additional preprocessing step could be applied during fiber tracking to improve tractography, e.g., filtering out false positive streamlines as applied in (Xu et al., 2019). However, such preprocessing would need additional anatomical information, e.g., from a T1-weighted image, as well as inter-modality image registration. In addition, we found that there was no obvious difference if short or long fiber streamlines tended to be misclassified (see Supplementary Experiments 3.3 for the length distribution of the misclassified fibers). One potential explanation is that the same number of points were sampled from each individual fiber streamline.

In related work, several methods have been proposed for deep learning tract segmentation. In voxel-based methods, tractography and tract segmentation are performed based on prediction of tract presence volumes, for example using spherical harmonics (Reisert et al., 2018) or fiber orientation distribution function (fODF) peaks (Wasserthal et al., 2018, 2019). In fiber-based methods, tractography fibers are directly classified for tract segmentation, for example based on a spherical brain reparameterizations (Gupta et al., 2017b, 2018), fiber spatial coordinates, and/or fiber shape features (Xu et al., 2019; Gupta et al., 2017a; Lam et al., 2018). Thus far, one deep learning tract segmentation method (TractSeg) has been demonstrated to be able to generalize to datasets acquired with different scanners and with multiple pathologies (Wasserthal et al., 2018, 2019). Our results in the ABIDE, HCP, CNP and PPMI datasets support this finding regarding the generalization of TractSeg. However, improved tract identification performance was obtained on the challenging dHCP and BTP datasets using DeepWMA. Performance of tract identification using DeepWMA was dependent on the type of input tractography. For example, in the dHCP dataset, where TractSeg could identify 68% of fiber tracts, the DeepWMA method was able to identify from 74% to 99.6% of tracts (using DTI and UKF tractography, respectively). The two-tensor UKF fiber tracking method is robust for tract segmentation across the lifespan (Zhang et al., 2018c) and is highly sensitive, especially in the presence of crossing fibers and peritumoral edema (Chen et al., 2015; Liao et al., 2017; Gong et al., 2018).

We demonstrated that DeepWMA provided a good generalization to multiple different fiber tracking methods. This is important because there are many available fiber tracking methods, and high variability across fiber tracking results (Maier-Hein et al., 2017; Catani and De Schotten, 2008) poses a challenge for tract segmentation. (For example, in both expert (Catani and De Schotten, 2008) and automated (Wassermann et al., 2016) region-of-interest (ROI) tract segmentation methods, additional ROIs are required for multi-fiber tractography due to increased sensitivity (O’Donnell et al., 2017).) Due to its robust performance, DeepWMA may be useful in the future for comparison of results across fiber tracking methods.

We showed that our DeepWMA method enables consistent white matter segmentation on tractography data from multiple populations with large anatomical variations. In particular, for the neonates and the patients with space-occupying brain tumors, their white matter anatomy varies significantly from the healthy adult population used for the training data curation. As a result, tractography fibers computed from the neonates and brain tumor patients have large local differences from those in the training tractography data. DeepWMA could handle such large individual anatomical differences, potentially due to the robustness of the proposed FiberMap to local fiber differences.

Potential future directions and limitations of the current work are as follows. First, a more comprehensive training dataset could be created to benefit research on additional tracts of interest. This could be done by annotating the non-outlier fibers currently in the category of “other fibers” into additional anatomically meaningful tracts (e.g. fornix, anterior commissure, and superficial fiber tracts). Second, given the fact that DeepWMA relies only on fiber spatial information (encoded in the FiberMap descriptor), it is straightforward to apply DeepWMA to train on labeled tractography data from sources other than the currently used ORG atlas. These sources could include tractography data from other curated databases or even other species. In particular, DeepWMA can enable inclusion of tractography data from multiple sources together, where different anatomical tract definitions and tractography algorithms can be used in each data source. In this way, a tract segmentation model would be learned to aggregate tract variability across the different sources. This could be important to handle potential issues such as inter-rater tract segmentation variability (Rheault et al., 2020) and inter-algorithm tractography variability (Ciccarelli et al., 2008; Zhan et al., 2015). Third, our current results demonstrated a highly consistent segmentation result across the different anatomical tracts under study. For example, we found that there was no obvious difference if short or long fiber streamlines tended to be misclassified (Supplementary Figure 3), and the classification accuracy of fiber tracts with complex shape (AF) and simpler shape (CST) was similar (AF with precision = 0.9 and recall = 0.91, versus CST with precision = 0.9 and recall = 0.89, computed in our training tractography data). However, an interesting further investigation could include a more comprehensive comparison across the different anatomical tracts. Fourth, in the present study, we aimed to demonstrate the application of DeepWMA for whole-brain tractography segmentation in a large dMRI test dataset. Therefore, we did not perform any statistical analyses for within- or between-cohort studies. Further work could include such studies to investigate population-specific characteristics of the tracts obtained from DeepWMA. Fifth, the creation of FiberMap includes flipping and repetition of existing data so that additional fiber point spatial information can be accessed and a deeper network architecture can be applied. However, we acknowledge that a more compact representation could be favorable, generating a comparable result while reducing computational burden, which can direct a potential future investigation. Sixth, in the present study, we explored a standard CNN architecture, which provided highly promising performance. Future work could include an investigation of more advanced network architectures to improve fiber classification accuracy.

5. Conclusion

We have presented a deep learning tract segmentation method for anatomical fiber tract identification from whole-brain tractography. Experimental results show successful application of the proposed method for fast and consistent tract segmentation across different dMRI acquisitions, across different populations (across genders, the lifespan, and different health conditions), and across different fiber tracking methods.

Highlights.

• A novel deep learning tract segmentation method with a new 2D multi-channel fiber feature descriptor

• Consistent tractography segmentation of subjects across the full lifespan

• Good generalization to tractography data from multiple different fiber tracking methods