Figure 1.

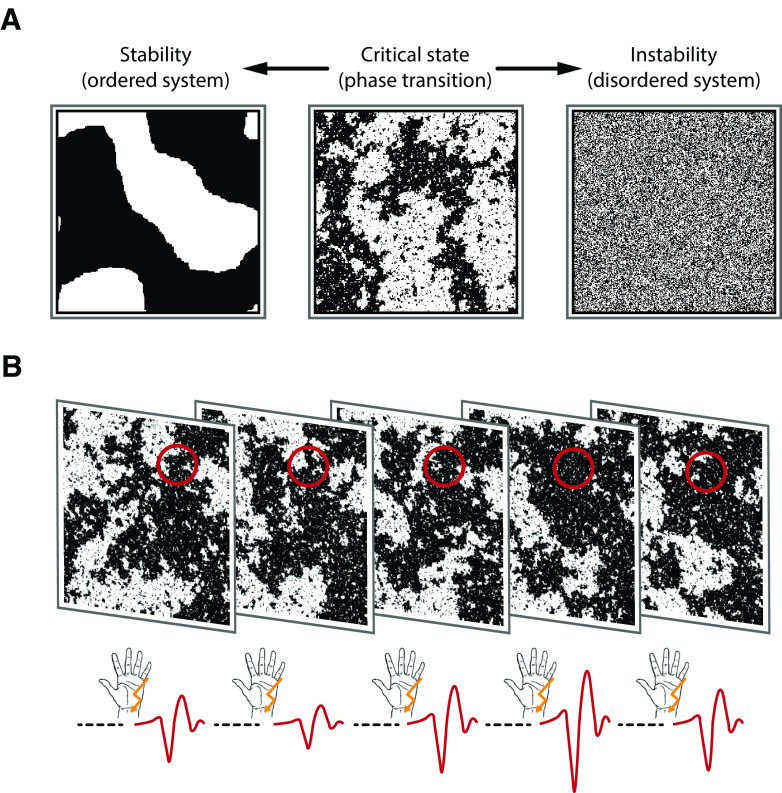
Types of system dynamics and how to probe them. A, Ising model at different system states: ordered, critical, disordered (from left to right). Transferred to a grid of neurons, black and white shades represent firing and nonfiring neurons, or, as in the context of our study, neurons that can or cannot be recruited by the stimulus. Here, snapshots of the system at a given point in time are shown. In an ordered system, local interactions dominate and lead to highly stable neural activity. In contrast, firing patterns in a disordered system are highly unstable and quickly change from moment to moment in a stochastically independent manner (i.e., white noise). At the critical state, the system resides at the border between the tendencies either toward an ordered or toward a disordered system. This is reflected by the spatiotemporal dynamics (i.e., scale invariance or power-law dynamics). Scale invariance is visible from the middle panel since similar clusters of black pixels occur on all scales. B, Experimental paradigm. The instantaneous state of the neuronal system (illustrated here with snapshots of the Ising model at the critical state) is probed by somatosensory stimuli. The amplitude of the N20 component of the SEP (negative peaks of the red curves at the bottom) is expected to be proportional to the number of neurons that can be recruited by the stimulus at a given moment (black pixels in the probed area, which is marked by the red circles), therefore reflecting a measure of instantaneous cortical excitability. In a stable system, the number of neurons that can be excited would barely change over time; whereas in an unstable system, this would vary randomly. However, at the critical state, configurations would show the largest range of variation over time with fluctuations following a temporal power law.