Origin of internal friction in disordered proteins depends on solvent quality

Abstract

Protein dynamics often exhibit internal friction, i.e. contributions to friction that cannot solely be attributed to the viscosity of the solvent. Remarkably, even unfolded and intrinsically disordered proteins (IDPs) exhibit this behavior, despite typically being solvent-exposed. Several competing molecular mechanisms have been suggested to underlie this phenomenon, in particular dihedral relaxation and intrachain interactions. It has also recently been shown that single-molecule data reflecting internal friction in the disordered protein ACTR cannot be explained using polymer models unless this friction is dependent on protein collapse. However, the connection between the collapse of the chain and the underlying mechanism of internal friction has been unclear. To address this issue, we combine molecular simulation and single-molecule experimental data to investigate how chain compaction affects protein dynamics in the context of ACTR. Chain reconfiguration times and internal friction estimated from all-atom simulations are in semi-quantitative agreement with experimental data. We dissect the underlying molecular mechanism with all-atom and coarse-grained simulations and clearly identify both intrachain interactions and dihedral angle transitions as contributions to internal friction. However, their relative contribution is strongly dependent on the compactness of the IDP: while dihedral relaxation dominates internal friction in expanded configurations, intrachain interactions dominate for more compact chains. Our results thus imply a continuous transition between mechanisms and provide a link between internal friction in IDPs and that in more compact and folded states of proteins.

Graphical Abstract

INTRODUCTION

Protein dynamics cover many orders of magnitude in time, from the sub-microsecond reconfiguration of unfolded proteins to the timescales of protein folding and molecular assembly extending to minutes and hours ¹. Since proteins function in the condensed phase, frictional forces strongly affect their dynamics. For high solvent friction, Kramers’ reaction rate theory predicts a simple first-power dependence of the relaxation time, τ, on the solvent viscosity η, τ ∝ η.² Deviations from this expectation were first demonstrated for proteins by Eaton and co-workers, who studied the vibrational relaxation of folded myoglobin as a function of solvent viscosity.³ Their finding that the relaxation time became less dependent on solvent friction at low solvent viscosities led them to propose an additive, solvent-independent contribution to the friction, arising from the protein, often referred to as “internal friction”. When the viscosity dependence of protein folding was investigated by Eaton and others, it was found that the effect of internal friction on folding rate varied from protein to protein. While in some cases, Kramers-like behavior was observed ^4–5, deviations from this relationship indicative of internal friction were found for other proteins ^{3, 6–9}. Simulation^10–11 and theoretical¹² studies have suggested that the origin of internal friction in protein folding can be attributed to the role of dihedral angles in the folding mechanism.

Most recently, it has become possible to study internal friction in unfolded, or intrinsically disordered proteins (IDPs) using single-molecule fluorescence experiments which probe the dynamics of intramolecular distance fluctuations. These studies have suggested that internal friction plays a significant role in the dynamics of disordered protein chains under folding conditions ^{9, 13–15}. The signature of internal friction in unfolded proteins has also been identified in molecular simulations, and several possible mechanistic contributions have been proposed, including intramolecular hydrogen bonding, concerted dihedral motions, and solvent memory effects ^15–18. In contrast to the complexity of folding reactions, the dynamics of unstructured polypeptide chains can be quantified ¹³ in terms of theories of polymer dynamics that explicitly include internal friction effects ^{13, 19}. Recently, four theories of polymer dynamics including internal friction were applied to single-molecule fluorescence data for the intrinsically disordered protein ACTR (activator of thyroid hormone response)²⁰. It was found that all the theories could describe the viscosity-dependent reconfiguration times of the protein under a given set of conditions ²¹. However, capturing the change of relaxation time as a function of protein collapse (either by varying denaturant concentration or changing pH), required that the internal friction parameter in each theory be dependent on the degree of collapse. Identifying the molecular mechanism of collapse-driven internal friction and its contribution relative to other factors will therefore require a close combination of experiment, theory, and simulation.

In this work, we use all-atom molecular dynamics simulation to understand the contributions to internal friction from the previously identified dihedral isomerization dynamics, from concerted dihedral motions and effects related to chain collapse. By manipulating the dynamics of dihedral flipping in the simulation we demonstrate that both dihedral isomerization and protein compaction influence the observed internal friction. In order to separate more clearly the contributions from dihedral dynamics and protein collapse, we employ a coarse-grained model in which the dihedral barriers and protein compactness can be easily adjusted. We find that both factors can alter internal friction of an IDP, with dihedral flipping being most important for expanded conformations and exclusion of solvent playing a larger role for compact conformations. Thus, the origin of the observed internal friction varies with the solvent quality.

METHODS

All-atom molecular dynamics simulations of ACTR in explicit solvent

The amino acid sequences of human ACTR (1018–1088) were run using all-atom simulations with Gromacs 4.6.7. ²² Simulations were set up at a constant temperature of 295 K using a velocity rescaling thermostat²³ with 0.1 ps coupling time and a pressure of 1 bar using a Parrinello-Rahman barostat. ²⁴ Electrostatic energies were calculated using particle-mesh Ewald summation ²⁵ using a 0.12 nm grid and real-space cut-off of 0.9 nm. Lennard-Jones interactions were calculated using a twin-range scheme with inner and outer cut-offs of 0.9 and 1.4 nm. The Amber ff03ws force field ²⁶ was used for the protein, with the TIP4P/2005 water model. ²⁷ The simulations were run with a rhombic dodecahedral box with ~6.5 nm shortest distance between periodic images.

A set of solvent viscosities were introduced by varying the water mass, similar to previous publications ^{16, 28–29}. The water mass, solvent viscosities and the corresponding time steps for molecular dynamics are shown in Table S1. The starting configuration was chosen from the last frame of a previous 200-ns replica exchange study ²⁶. The radius of gyration (R_g) was 2.2 nm for the initial configuration, close to the average R_g of the trajectory. This helps save computational time for equilibration. In normal solvent viscosity, the initial configuration was first equilibrated for 200 ps and was then run for 2 μs for analysis. For the other solvent viscosities, the same number of simulation steps were run compared to the normal solvent viscosity.

Simulations with restrained dihedral angles were realized using the dihedral restraints method in Gromacs with a harmonic spring constant of 500 kJ/mol/rad². Dihedral restraints were applied to all ϕ,ѱ backbone dihedral angles. Two sets of simulations were run, starting from one compact and one expanded structure from the previous simulations²⁶. The initial configuration was first equilibrated for 200 ps and was then run for 500 ns for analysis in normal solvent viscosities, and equivalent simulation steps in the other solvent viscosities.

Dihedral flipping time and concerted dihedral flipping time

In order to calculate the dihedral flipping time between states, dihedral angle states are assigned according to the backbone dihedral angles by the criterion as: extended state ϕ ∈ [−180, −40] Λ ψ ∈ [120,180] and helical state ϕ ∈ [−180, −40] Λ ψ ∈ [−60,0] for non-Gly residues; and extended state (ϕ ∈ [−180, −50] ∪ [50, 180]) Λ (ψ ∈ [−180, −150] ∪ [150,180]), helical state ϕ ∈ [−100, −40] Λ ψ ∈ [−60,0] and α_L state ϕ ∈ [50,110]Λ ψ ∈ [−50,70]. Transitions were counted when the trajectory moves from one of these states to another. The mean dwell time between transitions is defined as the dihedral flipping time.

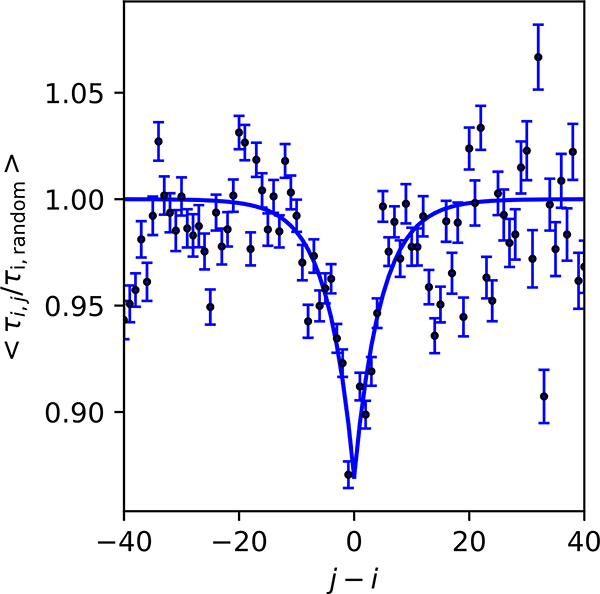
Potential correlations between transitions involving the backbone dihedral angles of the i-th and j-th residues (concerted dihedral flips) were identified via the mean waiting time τ_ij for the i-th residue to flip after the j-th residue flips. This was compared with the average time for a dihedral flip for the i-th residue τ_i,random, obtained by randomly generating starting times and then determining the waiting time to see the next dihedral flip event of residue i. For each residue, 10,000 randomly generated starting times were used to obtain the average time of a random dihedral flip. We then obtain the mean ratio $\langle \frac{{\tau }_{ij}}{{\tau }_{i,random}}\rangle$ as a function of j − i, shown in Fig. 3. If the ratio is smaller than 1, it means that the time for a concerted dihedral flip is shorter than the time of a random dihedral flip for a specific sequence separation j − i and therefore suggests a correlation between the dihedral flips of the i- and j-th residues. We then fit the ratio to an equation

$$\langle \frac{{\tau }_{ij}}{{\tau }_{i,random}}\rangle =1-\text{a}\cdot \exp \left(-\frac{|j-i|}{n}\right)$$

in which a and n are the fit parameters, and n is a measure of the number of sequential residues for which dihedral flips are correlated.

Figure 3.

Correlation between dihedral angle hopping times from MD-simulations, averaged over all viscosities. τ_ij is the average time between a dihedral flip of residue i and the next flip of residue j, and τ_i,random is the average time for the i-th residue to make a dihedral flip, starting from a random time. The black line is an exponential fit with a correlation length of 4.7 ± 0.8 residues (see Methods for details).

Molecular dynamics simulations of a homo-polypeptide with explicit solvent

Simulations of a 30-residue homo-polypeptide were run with Gromacs 4.6.7 ²² using a coarse-grained representation (one bead per residue) of the polypeptide and an all-atom representation of explicit solvent. Simulations were set up at a constant temperature of 350 K using a velocity rescaling thermostat ²³ with 0.1 ps coupling time and a pressure of 1 bar using Parrinello-Rahman barostat ²⁴. Electrostatic energies were calculated using particle-mesh Ewald ²⁵ using a 0.12 nm grid and real-space cut-off of 0.9 nm. Lennard-Jones interactions were calculated using a twin-range scheme with inner and outer cut-offs of 0.9 and 1.4 nm. The TIP3P water model was used for the explicit solvent ³⁰. The simulations were run with a rhombic dodecahedral box and ~6 nm shortest distance between periodic images. A set of solvent viscosities were introduced by using the same water mass scaling method as used in the all-atom simulations above. Each residue of the polypeptide was modeled with a Lennard-Jones potential of σ = 0.47 nm and ε = 5 kJ/mol. The bond length was 0.38 nm and was simulated with harmonic potential with a spring constant of 2.9×10⁵ kJ/mol/nm². The cosine-based angle potential in Gromacs was used with θ₀ of 90 degrees and a harmonic spring constant of 580 kJ/mol/rad². For the dihedral potential we adopted the statistical potential of an alanine residue used in a previous work ³¹. The simulation was first equilibrated for 200 ps and then run for 1 μs for analysis. The solvent accessible surface area (SASA) was calculated by using the Gromacs program “g_sas”.

Relaxation time of molecular dynamics simulations

The relaxation times of both all-atom and coarse-grained molecular dynamics simulations were analyzed using the autocorrelation function (ACF) C(τ) for the end-end distance and dihedral angles. The dihedral angles were first processed using a cosine function before calculating the ACF. The relaxation time on the coordinates was then calculated from a time integration of C(τ). To overcome the large uncertainties in the part of the ACF where it is close to 0, we only numerically integrate C(τ) where C(τ)>0.1 and extrapolate the integration of the tail by integrating an exponential decay fitted to C(τ) using the time range for which C(τ)>0.1. Error bars of the relaxation time are estimated using block averages of the trajectories, with 5 blocks.

RESULTS AND DISCUSSION

Internal friction in ACTR revealed by all-atom simulations

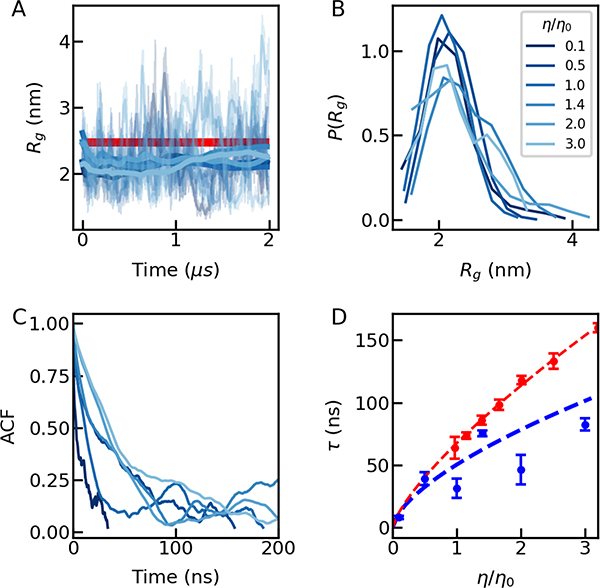
To identify the molecular origin of internal friction, we performed all-atom molecular dynamics (MD) simulations of ACTR at different solvent viscosities (Fig. 1). In the simulations, we vary viscosity by rescaling the mass of the water molecules (Table S1) ^{16, 28–29}, which leaves the protein free energy surface unchanged. ACTR was simulated for 2 μs, which is 30 times longer than the experimentally observed reconfiguration time ^{15, 21} and therefore expected to be sufficient for obtaining an equilibrium with respect to the properties of interest, i.e. distance distributions and dynamics for residue pairs well separated in sequence (see Methods section), resulting in a total of 10 μs of simulation data for the five viscosities studied. The resulting radius of gyration (R_g) of 2.2 ± 0.1 nm is close to the value determined by FRET here (Fig. 1A) and to previous measurements ^{15, 21, 32–33} (Table S2) and is similar across all solvent viscosities (Fig. 1A). The probability distributions of R_g (Fig. 1B) at different solvent viscosities are also similar, suggesting reasonable convergence of the simulations in sampling R_g. Even more importantly, the end-to-end chain reconfiguration times from the simulations (Fig. 1C and D) are within a factor of two of the values obtained from nanosecond fluorescence correlation spectroscopy measurements (ns-FCS) at normal solvent viscosity (64 ± 9 ns in the experiment and 32 ± 8 ns in the simulation). The reconfiguration times show a clear increase with increasing solvent viscosity, as in experiment (Fig. 1D).

Figure 1.

Dimensions and dynamics of ACTR obtained from all-atom molecular simulations and single-molecule FRET experiments. (A) Trajectories of the R_g of ACTR from MD-simulations at different viscosities; thick lines show averages with a moving window of 1 ns. The estimate from experiment ²¹ is shown in red (see Table S2). (B) The probability distribution of R_g. The legend shows the solvent viscosity. (C) The corresponding end-to-end distance correlation functions as a function of solvent viscosity; (D) Reconfiguration times from simulation (blue) and single-molecule FRET experiments (red).

However, neither in experiment nor simulation are the relaxation times τ proportional to viscosity η, as expected from high friction Kramers theory. The deviation from the expected τ ∝ η behaviour has essentially become an operational definition of internal friction, and two alternative methods have previously been used to quantify it. In the first, a friction component resulting from interactions within the protein has been invoked³, which effectively leads to an additive timescale that is independent of the viscosity of the solvent ³⁴. For unfolded proteins, this additivity of time scales results from Rouse- or Zimm-type models of polymer dynamics with internal friction.^{13, 35} In practice, one can linearly fit the relaxation time as a function of the solvent viscosity and obtain the relaxation time extrapolated to zero viscosity, τ₀, through the fit. Then internal friction can be quantified by the relaxation time at zero viscosity or its value relative to the relaxation time at normal viscosity, α = τ₀/τ(η₀). In the second method, if a power law relation between relaxation time and solvent viscosity is assumed, a weaker viscosity dependence such as τ∝η^β with β < 1 has been found to describe the experimental data ^{4, 36–37}. The range of accessible solvent viscosities is often limited, which complicates an experimental discrimination between these two forms. It was found in several recent works that quantifying the deviation from simple Kramers-like behavior using either the additive timescale normalized with by relaxation time in normal viscosity (i.e. α), or the exponent β from a power-law relation between relaxation time and solvent viscosity yield qualitatively similar conclusions ^{10, 38}. In the current work, we will use β to quantify the internal friction of IDPs in both simulation and experiment and provide all the α and τ₀ values in the Supporting Tables.

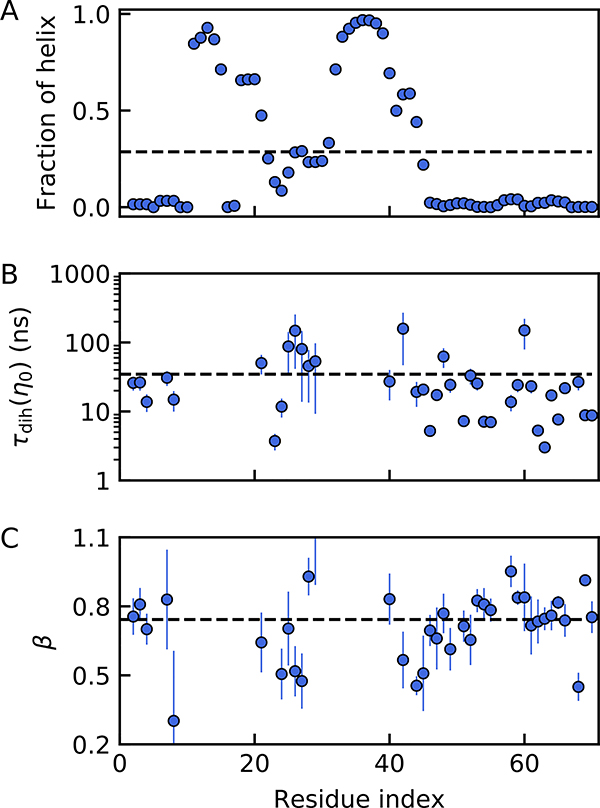
The fitted exponent β = 0.64 ± 0.13 (Fig. 1D and Table S3) from simulation is similar to the experimental value of 0.75 ± 0.02, suggesting that the simulation captures the essential features of our experiment. The remaining deviations between the absolute times may be due to an increased content of residual helical structure of ACTR in the simulations (~ 30%) (Fig. 2A). For example, > 90% residual helical structure was found in the region of α-helix 1 (residue 27–39), whereas only 12 – 60% was found experimentally by NMR from secondary chemical shifts ^{32, 39}. Reproducing equilibrium helical propensity for specific regions of the protein requires more extensive simulations. Indeed, we find that helical propensity is much closer to experiment in a replica exchange simulation, ²⁶ as expected given the accurate reproduction of helical propensity by this force field in other contexts^{26, 40}. However, as our interest is in dynamical properties, replica exchange simulations are not applicable here.

Figure 2. Analysis of the dihedral angle flipping times from all-atom molecular dynamics simulations of ACTR.

(A) Average secondary structure content as a function of the residue position. (B) Dihedral flipping times in normal solvent viscosity. (C) The exponent of power-law fits to the dihedral relaxation time dependence on solvent viscosity. The thick dashed lines indicate the average values for the entire chain in each plot.

Role of dihedral dynamics in internal friction

A commonly invoked source of internal friction in polymers and unfolded polypeptide chains is activated bond rotation along the chain ^{17, 41–42}. Moreover, recent simulations on short polypeptides and model compounds have indicated that individual dihedral angle flipping rates can have surprisingly weak solvent viscosity dependencies ²⁸. We interpreted this deviation from Kramers theory as arising because the time scale of water relaxation associated with solvent friction is comparable to that of the barrier-crossing event itself. In this case, Kramers theory ², which assumes that friction forces are uncorrelated in time, is not applicable, and Grote-Hynes theory ⁴³ provides a better description with a weaker viscosity dependence. Recent work by Netz and co-workers also identified a strong contribution of internal friction to the dihedral dynamics of butane, the simplest model for dihedral isomerization. By directly computing the friction kernel for the dihedral angle, they found that this friction arises mainly from coupling to other intramolecular degrees of freedom in the molecule.¹¹

We therefore analyzed the dihedral angle flipping time in our simulation on a residue-by-residue basis and observe that the flipping times vary by three orders of magnitude along the sequence (Fig. 2B, see Methods for calculation of flipping time). A comparison of the variability with the residual helix content shows that residues in helical segments rarely flip during the simulation, as expected. For example, the dihedral angles of residues 4, 16 and 65 never flipped in the simulations of all six solvent viscosities. However, dihedral angles of 38 residues flipped at least 5 times in each solvent viscosity, providing sufficient statistics for further analysis. Large variability of the dihedral angle flipping times is still observed in the unstructured C-terminal segment of ACTR (Fig. 2A and B), indicating a significant impact of neighboring residues and local interactions on the flipping times even in the absence of persistent secondary structure. Intriguingly, the average waiting time of dihedral flipping events (35 ± 13 ns) is very close to the end-end chain relaxation time of 32 ± 8 ns at normal solvent viscosity. This would be consistent with a recent simulation study on shorter peptides which suggested that, because dihedral relaxation is much less sensitive to solvent viscosity than the characteristic Rouse time, dihedral relaxation is most likely to dominate the end-end distance correlation time at low viscosities ¹⁸. In that scenario, the two times can be comparable, although not necessarily equal¹⁸.

To quantify the viscosity dependence of the dihedral angle flips, we use the empirical power law to extract the exponents, β, for each residue separately. Of the 38 residues with sufficient flipping events (> 5), the large majority yield β < 1, resulting in an average of β = 0.74 ± 0.15 (Fig. S1). The weak viscosity dependence observed in the dynamics of the whole chain is also preserved in the dynamics of the individual dihedral angle flips, suggesting that dihedral angle flips indeed contribute substantially to internal friction effects on the length scale of the whole protein (Fig. 1B & 2C).

A second aspect of dihedral transitions is that they may become concerted under certain conditions, i.e. flipping of one torsion angle necessitates flipping at least one other. This effect was found to have a strong impact on the chain dynamics of compact polypeptide chains¹⁷. To elucidate whether correlations between dihedral angle flips also contribute substantially to the dynamics of ACTR, i.e., a more expanded chain in theta solvent, we computed the time between a dihedral angle flip of residue i and j from the simulation and compared that with the time of observing a dihedral angle flip from a random starting point (Fig. 3, see Methods for details of the calculation). This is similar to comparing the distributions of concerted dihedral flip times and individual dihedral flip times in a previous work¹⁸, but we have analyzed all possible sequence separations. The analysis shows that dihedral angle flips of a given residue occur slightly more frequently (~ 10%) if a bond j in the vicinity of bond i rotated. However, the correlation is weak and decays rapidly over a sequence separation of 4.7 ± 0.8 residues (using an exponential fit to the data in Fig. 3), indicating that concerted dihedral angle flips likely play little role in the dynamics of ACTR. This is possible because a single flip in an open chain can be accommodated by relaxing the chain via other mechanisms over many residues rather than requiring additional torsion angle flips. By contrast, in a compact chain in which this phenomenon was observed¹⁷, the segment containing the flipped torsion angle has much less freedom to relax, making flipping of a second torsion angle more likely. We therefore suggest that successive dihedral flipping dynamics have a limited effect on the internal friction of the end-end distance relaxation time of a disordered/unfolded chain with expanded conformation.

All-atom simulations distinguish dihedral and contact contributions to internal friction

Despite the evidence presented above for the importance of dihedral flipping in internal friction, there is experimental evidence for additional contributions from other mechanisms. It is possible to vary the degree of collapse of unfolded and intrinsically disordered proteins via additives such as guanidinium chloride (GdmCl), urea, salt, and osmolytes ^44–47. Previous work with single-molecule FRET has shown that lowering the concentration of denaturants such as GdmCl or urea results in chain collapse, with a concomitant increase in reconfiguration time.^{9, 13} This increased reconfiguration time is the opposite of what is expected from the Rouse theory of polymer dynamics, leading to the suggestion that this increase results from an increase in internal friction for more collapsed chains at low denaturant concentration.¹³ A similar increase in reconfiguration time was also observed for ACTR as the concentration of urea was lowered; when this data was fitted with four different polymer models which included internal friction, it was found that an increase in the internal friction parameter with decreased urea concentration was required in order to describe the data.²¹ In addition to protein collapse, however, the reduction in friction may arise from a smoothening of the energy landscape due to denaturant binding to the polypeptide chain at higher denaturant concentrations. ^48–50 To test for this, the dimensions of ACTR were also changed by altering the strength of the electrostatic interactions within the chain.²¹ By lowering the pH from 7.1 to 2.1, the helical content was increased and R_g was decreased from 2.7 nm to 1.7 nm, close to the estimated globular dimensions of the chain (1.3 – 1.4 nm), as a consequence of lower net charge. Reconfiguration times from ns-FCS showed that increasing compaction resulted in a slowdown of chain dynamics and apparent increase in internal friction, analogous to the case for denaturants. Thus, it seems that chain collapse by itself is sufficient to increase reconfiguration times for more compact chains, although an additional contribution from denaturant binding and secondary structure formation cannot be ruled out.

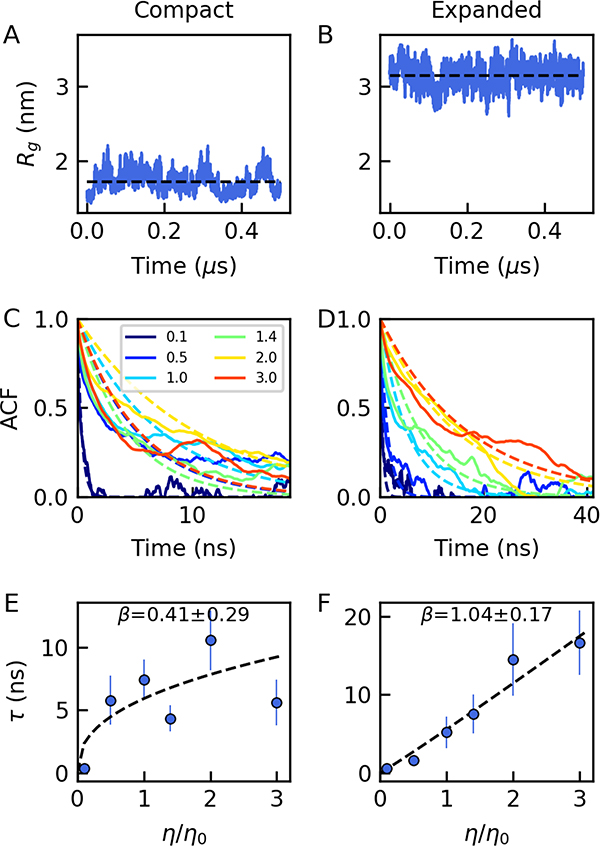
To separate the impact of chain dimensions on internal friction from the effect of possible dihedral angle flips in the atomistic model, we randomly chose one compact and one expanded conformer from the simulated distribution of ACTR molecules and performed additional simulations with harmonically restrained dihedral angles (see Methods) to prevent dihedral angle flips altogether (Fig. 4A and B). In these simulations, the amplitude of the end-to-end distance fluctuations is diminished by ~ 84% and ~74% in the compact and expanded configurations, respectively, compared to unrestrained simulations. The end-end distance relaxation time with restraints on dihedral angles is also shorter than an unrestrained simulation or experiment (Fig. 1), because restraining dihedral flips also reduces other degrees of freedom of the peptide in simulations. We will address these limitations by removing dihedral barriers instead of restraining the dihedral flips in a coarse-grained model in the following section. However, the remaining fluctuations due to bond stretching and bending are sufficient to result in a clear decay in the end-to-end distance correlation function (Fig. 4C and D). Most remarkably, our simulations at different solvent viscosities do not reveal any sign of internal friction for the expanded conformer (β = 1.04 ± 0.17) (Fig. 4F and Table S3). In contrast, the simulation of the compact conformation with restrained dihedrals results in a much reduced viscosity dependence, with an exponent of β = 0.41 ± 0.29 (Fig. 4E and Table S3), indicative of internal friction. This could be due to the increasing frequency of intrachain interactions in a compact protein, similar to what was observed in a previous work showing different internal friction behaviors for different intrachain interactions in a compact folded protein⁵¹.

Figure 4.

All-atom ACTR simulations with harmonically restrained dihedral angles. (A, B) Trajectories of the R_g are shown for (A) a compact and (B) an expanded conformation of ACTR, respectively, at normal water viscosity; (C, D) The corresponding end-to-end distance correlation functions as a function of water viscosity (water mass scaling coefficients shown in legend); (E, F) The corresponding relaxation time dependence on solvent viscosity, with the fitted power-law exponent in the legend.

A simple model further reveals the origins of internal friction in ACTR

To explore the effect of compaction on the polypeptide dynamics in a more generic and comprehensive manner, we used a coarse-grained model of a homo-polypeptide in explicit solvent with the TIP3P water model ³⁰ (referred as coarse-grained model hereafter). Here, each residue is represented by one bead interacting with the other beads and the solvent via Lennard-Jones potentials. Bond, angle and dihedral potentials for coarse-grained alanine peptides ³¹ were used. (See details in Methods). The advantage of such a coarse-grained model is two-fold: first, the potential energy is more easily tunable so that we are able to test the contributions of dihedral flips and chain compaction; second, sampling becomes orders of magnitude less demanding compared to the all-atom simulations, and therefore we can quantify internal friction with much more confidence. We performed simulations of this model with different pair interaction strengths between peptide and water, expressed by the scaling factor λ_pw. With decreasing λ_pw, the chain collapses to a dense globule, which is evident in both R_g and the length scaling exponent v (Fig. 5A and Fig. S2). For different degrees of compaction, we then performed simulations at different solvent viscosities to elucidate the change in the reconfiguration time of the chain and the fractional viscosity exponent β characterizing the viscosity dependence.

Figure 5.

The effect of intra-chain interactions in a coarse-grained model. (A) The R_g (left axis) and the scaling exponent ν (right axis) of the coarse-grained polypeptide as a function of increasing peptide-water interactions. λ_pw is the scaling factor of the pair interactions between the peptide and water. The scaling exponent ν is calculated by fitting a power-law to the dependence of root-mean-squared distance between i and j-th residue on sequence separation |i-j| (Fig. S2). (B) Solvent accessible surface area (SASA). (C) The power-law fitting exponent (β) characterizing the dependence of relaxation times for the end-end distance (blue) and dihedral flips (red) on solvent viscosity. (D) The relaxation time of the end-end distance (blue) and dihedral flips (red) in normal solvent viscosity (η₀). In all figures, we show results from R_g-restrained simulations with a target value of 0.5 nm with filled upper triangle symbols and 0.7 nm with lower empty triangle symbols (Table S7). Where not visible, error bars are smaller than the symbol size.

We find a drastic increase in the reconfiguration time with increasing compaction of the chain (Fig. 5D), in accord with our experimental data at different pH-values²¹. In addition, β decreases from ~1 to ~0.4 with increasing compaction of the chain, indicative of increased internal friction (Fig. 5C). Thus, similar to the all-atom simulations of single conformers (Fig. 4), we find higher internal friction in more compact conformers. In addition, the dihedral angle flipping time becomes slower despite an unaltered potential energy for dihedral flips (Fig. 5D and Table S4). This is mostly because chain compaction constrains the possible flips which can occur, resulting in an effective increase in the free energy barriers for dihedral flipping (Fig. 5D and S3). Following the trend of reconfiguration times, the viscosity dependence of the dihedral angle flipping times also becomes weaker with increasing compaction of the chain (Fig. 5C), suggestive of increasing internal friction at the level of individual dihedral angle flips.

Increasing dihedral barriers

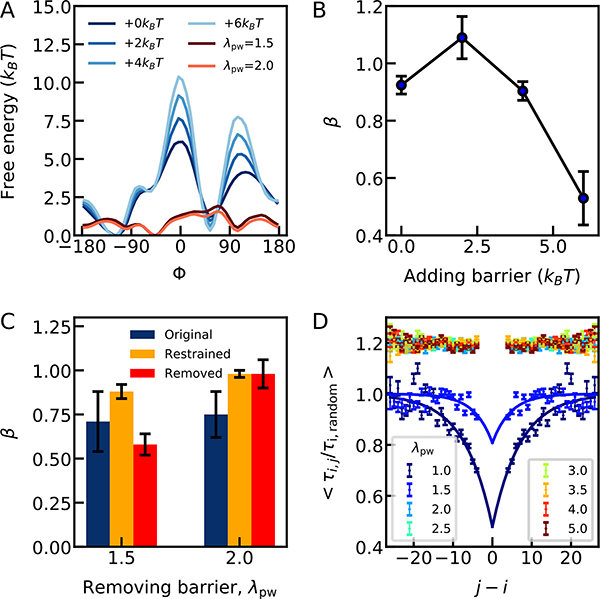
To investigate how the transitions across torsional barriers affect internal friction, we first increase the barriers in the dihedral potentials for the case of an expanded chain with limited internal friction (λ_pw = 3.0 and β = 0.95 ± 0.03). To this end, we only change the barrier heights of the dihedral angle potential while preserving as closely as possible the positions of the free energy minima. This procedure leaves the dimensions of the chain unchanged within 2%, so any change in internal friction may be attributed to dihedral barrier crossings. Indeed, we observe an increased contribution of internal friction to the end-to-end relaxation time of the chain with increasing dihedral barrier height (Fig. 6A and B, and Table S5). A high dihedral barrier will tend to increase the internal friction of the unfolded chain due to the sharper barrier top and shorter barrier crossing time. This is in agreement with previous work ³⁸ using Grote-Hynes theory ⁴³ and solvent memory effects to understand the relation between dihedral barrier crossings and internal friction.³⁸ Another reason for the increased contribution of dihedral flips to internal friction may be that, with higher barriers, the time scale for dihedral flipping becomes closer to the overall relaxation time, as proposed by Makarov and co-workers.¹⁸

Figure 6.

The effect of dihedral barriers on the internal friction in the coarse-grained model. (A) The dihedral barriers for different cases tested. Blue curves: barriers which were increased by modifying the dihedral potential, (ϕ) (note in this bead model, there is only one type of dihedral, i.e. ϕ does not have the standard meaning for an all-atom polypeptide), using protein-water scaling λ_pw of 3.0. Red curves: dihedral barriers after being made as flat as possible by adding a four-term compensating Fourier series. A separate set of terms were used for protein-water scaling factors λ_pw of 1.5 and 2.0, since the original free energy barrier varies with the degree of collapse. (B) The dependence of the power-law exponent (β) on the barrier height for simulations with raised barrier with λ_pw of 3.0. (C) Effect on power law exponent β of either removing or restraining dihedral angles (see legend), for simulations at protein-water scaling factors λ_pw of 1.5 and 2.0, representing two different degrees of collapse. (D) Correlation between dihedral angle hopping times for the bead-model (analogous to Fig. 3 for all-atom model). τ_ij is the average time between a dihedral flip of residue i and the next flip of residue j, and τ_i,random is the average time for the i-th residue to make a dihedral flip, starting from a random time. The colored lines are exponential fits for the data at λ_pw of 1.0 and 1.5, yielding correlation lengths of 7.1 ± 0.6 and 4.6 ± 1.2 residues, respectively (see Methods for details). For clarity, the data sets at the other λ_pw, are offset by 0.2 on the y-axis. These data show no evidence of correlation.

Concerted dihedral flips

We revisit the remaining question of concerted dihedral flips that arose from the all-atom ACTR simulations. In the simulation of an extended conformation, we saw limited evidence of concerted dihedral flips. Here in the coarse-grained model, we generate chains with different compactness by scaling the peptide-water interactions (λ_pw). As shown in Fig. 6D, we find virtually no evidence for concerted dihedral flips for all the data sets with λ_pw>1.5 and a corresponding scaling exponent of larger than 0.4, consistent with our observation from the all-atom ACTR data. For λ_pw=1.5 and 1.0, we see increasing correlation lengths with increasing compactness, suggesting that concerted dihedral flips can only be observed when the peptide is very compact and has limited access to other relaxation mechanisms, making flipping of a second torsion angle more likely.

Freezing/removing dihedral flips

In analogy with the all-atom simulations, we also simulated chains with harmonically restrained dihedral angles based on one compact and one expanded configuration. Consistent with the all-atom ACTR-simulations, freezing the dihedral flips effectively removes internal friction in the expanded configuration, but it is not clear whether internal friction is still present in the compact configuration due to the uncertainty in β (Table. S6). However, the homo-polypeptide model allows us to go one step further by adding a compensating potential function which effectively removes the dihedral barrier to < 2 k_BT. In practice, we modify the dihedral barrier by adding a fourth order Fourier series to make the free R1.3 energy for dihedral flips as close to flat as possible (Fig. 6A). Simulations with this potential allow us to examine the influence of barrier crossing events in both compact and expanded states (note that because of the already-slow dynamics in the compact state, we could not increase the barriers in this case). Indeed, as shown in Fig. 6C, internal friction is significantly less prominent after removing dihedral barriers in the expanded state (λ_pw = 2.0). However, in the compact state with lower dihedral barriers (λ_pw = 1.5), internal friction remains high. Hence, the simulations with reduced dihedral barrier heights suggest that factors other than dihedral barrier transitions contribute to the internal friction in the compact state ¹⁶.

Collapsing the chain

Finally, to check whether the increased strength of intra-chain interactions is responsible for internal friction in the collapsed state, we confined the chain with favorable peptide-water interactions, i.e., a low tendency to form intrachain interactions (λ_pw=5.0), to a small volume by applying an external potential to R_g. The R_g restraint is introduced by $E_{\text{restraint}}=\frac{k}{2}{(R_g-R_{g,\text{targeted}})}^2$ using PLUMED 2.2.1 ⁵². Two sets of simulations were performed, with the same harmonic spring constant k of 2000 kJ/mol/nm², but different values for the targeted R_g of 0.5 and 0.7 nm, respectively. If internal friction in compact polypeptide chains arises from attractive intrachain interactions, we expect to find negligible internal friction in this case.

Indeed, the simulations show only a small increase of internal friction when collapsing the peptide (triangles in Fig. 5C and Table. S7) for both cases with different R_g,targeted, suggesting that chain collapse itself does not induce internal friction. Further support for this interpretation comes from analysis of the solvent accessible surface area (SASA). In the absence of confinement (Fig. 5A and B), SASA closely correlates with the R_g of the chain, as expected. However, in the simulations of confined chains with favorable peptide-water interactions, the average SASA is comparable to that from simulations without the restraint, despite the large reduction in R_g. Remarkably, although the two simulations with different R_g,targeted are very similar in R_g, SASA, and lack of internal friction, their end-end distance relaxation times at normal solvent viscosity differ by a factor of ~5 (Fig. 5D, Fig. S4A and Table S7). This suggests that we have almost reached the smallest R_g the peptide could adopt in both R_g-restrained simulations. The R_g in the case with a strong peptide-water interaction (λ_pw=5.0) is expected to be larger than that with a weak peptide-water interaction (λ_pw=1.0) due to the retained solvation. A small increase in volume confinement close to the limit results in the abrupt slowing down of the end-end distance relaxation, however does not impact internal friction. This suggests that the change of the chain relaxation time due to chain collapse does not correlate with internal friction defined as a deviation from proportionality of relaxation time and solvent viscosity. We note that the relaxation time for R_g is much less affected by confinement than end-end distance (Fig S5). This is probably because the fluctuations in R_g are very small due to the potential, so this coordinate can relax by local fluctuations only; longer timescale relaxation of the chain due to global rearrangements (as required for end-end distance relaxation) would contribute a very small amplitude to the correlation.

It is interesting to compare our results to very recent simulations of short Gly-Ser peptides confined in boxes of decreasing size⁵³. Similar to what we observe here for the confined bead model, the reconfiguration times increased abruptly upon compaction (Table S4), with a concomitant increase in dihedral angle free energy barriers (Fig. S3). However, in contrast to the behavior of our coarse-grained model, long-tailed distributions of relaxation times and pronounced anomalous diffusion were found for the confined Gly-Ser peptides, suggesting pronounced energetic trapping, possibly by directional interactions such as hydrogen bonds that are absent in our model.

Taking into account all the observations above, we conclude that internal friction in compact states is not caused by chain compaction alone, but rather by attractive intrachain interactions which reduce the solvent accessible surface area, and consequently the role of solvent friction in the dynamics. Hence, while dihedral angle flips dominate internal friction in expanded chains, attractive intrachain interactions can cause internal friction upon compaction of the chain. Similar to the internal friction effects identified in folded Myoglobin after laser-flash photolysis of carbon monoxide originally proposed by Eaton and co-workers³, the partial solvent shielding of residues in the interior of a compact chain decouples the formation and breakage of interaction between different chain segments from the dynamics of the solvent.

CONCLUSIONS

Internal friction, operationally defined as a deviation from Kramers theory ², has been observed in the native-state dynamics of myoglobin ³, in the dynamics of the proteasome ⁵⁴ and other enzymes ⁵⁵, in protein folding reactions ^{6–7, 56}, in the dynamics of unstructured peptides ⁵⁷, and in unfolded and intrinsically disordered proteins ^{9, 13, 15}. The molecular interpretations of internal friction are also highly varied. Previous interpretations range from solvent-decoupled processes in the solvent-inaccessible interior of proteins or partially structured transition states^{3, 9, 54, 56} to a break-down of continuum hydrodynamics and the insensitivity of local torsional transitions to solvent viscosity ^{3, 9, 12, 17, 28, 54, 56, 58–59} up to combinations of the two ^15–16.

In this work, we focused on the dynamics of the intrinsically disordered protein ACTR. We found that dihedral angle flips and interactions between non-local chain segments both contribute to internal friction in ACTR. However, the molecular origins of the two contributions are very different. Dihedral angle flips play a role because of they are intrinsically weakly sensitive to solvent friction. Importantly, effects from correlated dihedral angle flips, which have been shown to contribute substantially to the overall dynamics of compact polypeptides ¹⁷, play only a minor role in expanded protein chains. In ACTR, the correlation length does not exceed 5 residues and the correlation remains weak. The effect of transient interactions is more difficult to capture. Reduced solvent accessibility of chain segments in the collapsed state, which weakens the sensitivity to the bulk viscosity appears to contribute to the observed effect.

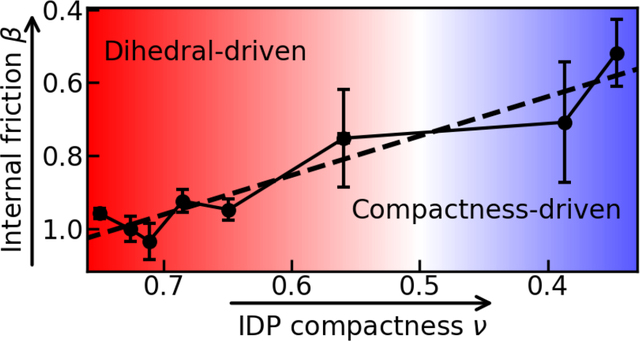
We further show that the dominant contribution (i.e. local dihedral isomerization, intrachain interactions, or both) varies with the degree of chain collapse. At low chain densities, the nonlinear viscosity dependence of the dihedral angle flipping dynamics dominates, leading to a deviation of the chain relaxation times from linear viscosity dependence. In compact conformations, in contrast, the probability of intrachain interactions increases together with an effective shielding of chain segments from the solvent: thus, the global chain dynamics are only moderately affected by the viscous drag of the solvent. The transition can be characterized in terms of the polymer length scaling exponents in our coarse-grained simulations with explicit solvent, which are a size-independent measure of chain compaction. We find that the length scaling exponent is near 0.5 (in the middle between λ_pw = 1.5 and 2.0 of the coarse-grained model), close to the Θ-state of the chain, i.e., conditions at which intrachain interactions and chain-solvent interactions balance ⁶⁰. Since previous results have indicated that aqueous conditions are often close to the Θ-solvent condition for unfolded proteins ^{33, 49, 61–66}, the two sources of internal friction identified in this study are likely to be ubiquitous for natural polypeptide chains. The idea of a constant, viscosity-independent friction component that adds to the friction of the solvent, as originally inferred from the active-site dynamics of myoglobin ³ and as assumed in the Rouse or Zimm models with internal friction ^{9, 13, 19, 35}, are well suited for quantifying the contribution of internal friction at a given degree of chain collapse. However, capturing the dependence of internal friction on chain compaction is likely to require the different molecular mechanisms and their relative contributions to be accounted for explicitly.

ABBREVIATIONS

IDP

intrinsically disordered protein

FRET

Förster resonance energy transfer