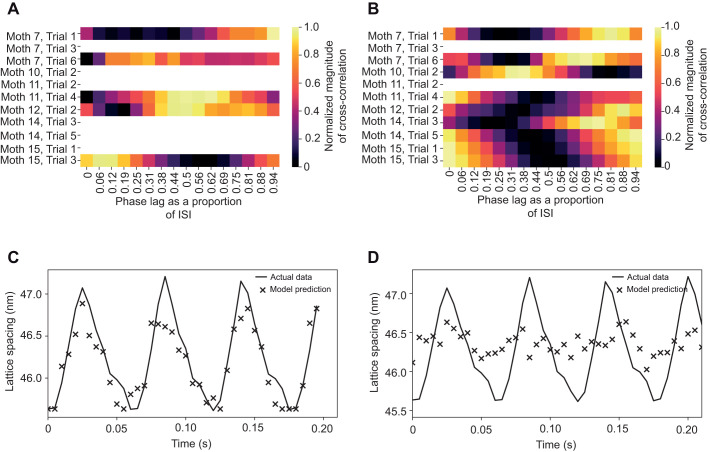
Fig. 3.

The relationship between lattice kinematics is not consistent across trials. (A) Cross-correlation of cross-bridge recruitment and thick filament stretch.There is not a consistent phase offset between cross-bridge recruitment and filament extension. The magnitude of the cross-correlation is normalized, and phase offset is measured in proportion of the interspike interval (ISI; the period of time between subsequent muscle activations). Some trials do not contain adequate data for all data pairings – a permutation bootstrap was used to determine for each datatype within a trial if it contained a significant periodic component at wingbeat frequency, and those that did were included. Correlation as a function of time lag in seconds can be found in Fig. S5. (B) Cross-correlation of cross-bridge recruitment and lattice dilation. (C) A mechanism-free model creates a good prediction of lattice spacing change on untrained lattice spacing data when it is trained and tested using data from the same trial, but different time points. Prediction for the case where the model is trained on 75% of a trial's data, and tested on the other 25%. The average RMSE was 0.27 nm. (D) The same mechanism-free model framework fails to create an adequate prediction of lattice spacing change when the model is trained on all trials but one and tested on the withheld trial. Representative image from the case where the model was trained on the data from all trials, except for one that was withheld as a test set. The average RMSE across all trials trained in this manner was 0.79 nm. The disparity between the model's performance under these paradigms suggests that while this model is capable of making good predictions from these types of data sets (C), the predictions made by the model cannot extrapolate effectively across individuals for this data set (D).