Skip to main content
NCBI home page
Journal of Orthopaedics logoLink to Journal of Orthopaedics
. 2020 Aug 27;22:390–396. doi: 10.1016/j.jor.2020.08.021

Simulation of L-4 lumbar spine model of motorist exposed to vibration from speed hump

B Jain A R Tony a,∗, MS Alphin b, G Sri Krishnan b
PMCID: PMC7490553  PMID: 32968339

Abstract

Background

The motorcycle is often used in recurring travel between locations, dense traffic, poor conditioned roads and thus the repetitive loading on the musculoskeletal system of the rider leads to risk factors associated with musculoskeletal disorders. This study was aimed to examine the biomechanical response of the L-4 lumbar spine while riding the motorcycle on the speed hump at 20 km/h.

Methods

Three-dimensional (3D) model of the L-4 lumbar spine was reconstructed based on the CT scan data obtained from the subjects. Material properties of the L-4 lumbar spine were assumed to be isotropic and homogenous. Mesh convergence and sensitivity analyses were performed and validated before simulation. Static and dynamic analyses were accomplished using quasi-static and steady-state dynamic analyses.

Results

Static analysis results show that the highest stress concentrations were found around the pedicle and spinal canal. It is an expected commonplace for injuries because of loading. The dynamic simulation results showed the major resonance of the L-4 lumbar spine model is about 8–40 Hz. The stress, displacement, velocity, and acceleration value declines beyond 40 Hz as the frequency increases.

Conclusions

The simulation specifies the symmetric and unsymmetrical distributions of vibration magnitude regions of the lumbar spine. This study provides the modelling of the lumbar spine (L-4) and validated the effect of overloading failure as well as identified the biomechanical behaviour.

Keywords: Lumbar spine, Mesh convergence, Sensitivity analysis, Quasi-static, Steady-state dynamic analysis

1. Introduction

Motorbikes are highly applicable for day today activities to move freely without much effort and used in regular basics for commuting, sports, and other economic activities.1 However, there are several benefits included in riding a motorbike, there are even more risks due to vibration, noise, and other environment factors.2 The continuous use of motorbikes leads to musculoskeletal disorders such as lower back pain, spine injury and disc dislocation.3 Improper posture, repeated body movements and stress while driving causes Driving related Musculoskeletal Disorders (DMSD). DMSD is highly related with spinal injury due to vehicle body vibration and other conditions.4,5 Lower back pain is also another common driving related musculoskeletal disorder among motorbike riders.

Computational biomechanics approach using simulation was suggested by many researchers to overcome these difficulties.6,7 Finite element (FE) analysis is normally used to understand the biomechanics of human lumbar spine.8,9 FE analysis is also accomplished to predict the biomechanical behaviour of bones and soft tissues.10 FE analyses have higher accuracy in results and lower in cost with in-vitro and in-vivo experiments.9 Several researchers’ have developed various lumbar spine FE models in the literature. The vertebrae are interlocking bones that form complex based structure and difficult to understand the mechanical properties.11,12 Geometry based L1-L5 lumbar spine model was developed using computerized tomography (CT) and validated with in-vitro 45 experimental data.13,14 L3-S1lumbar spine model was developed using CT scan for cadaveric male subject and validated with experimental results.15 Lumbar spine FE model (L1-L5) was used to identify the effect of dynamic behaviour of spinal fixators.16

L1-L5 lumbar spine FE model was developed to understand the biomechanics during replacement of discs and screw-based surgery.17 Schmidt et al. (2012) created a L1–L5 lumbar spine FE model using CT scan to predict the spine biomechanics after multilevel implantation.18 Lumbar spine model was developed to predict the optimal posture during different stress under compression, pure moment and bending.19 The effect of degenerated intervertebral discs on the lumbar spine (L1-S1) was developed using CT scan of 26-year old male healthy subject.20 Several authors have developed the lumbar spine to understand the biomechanical behaviour for various conditions. This study was aimed to create a lumbar spine bone (L-4) 3D model of the motor bike rider to identify the biomechanical behaviour while riding in the speed humps. Static and dynamic analyses were performed to estimate the biomechanical response of the lumbar spine model. The objectives of the present study are, 1) to estimate the input force transmitted to the vehicle seat while riding in the speed hump, 2) Quasi-static analysis was performed to estimate the stress, strain and displacement of lumbar spine, 3) Modal analysis and steady-state dynamic analysis were performed to estimate the modal frequencies and corresponding stress, displacement, velocity and accelerations of lumbar spine.

2. Methods

2.1. Subjects

Twelve male subjects who were between the ages of 18–28 volunteered to participate in experiment. The subjects had no history of musculoskeletal disorders and were not allowed to do any difficult physical activity on the day of measurement. This research has been approved by the IRB of the authors’ affiliated institutions. The detail description of the experimental procedure was explained to all the subjects before the experiment started. Measuring tape, gonimeter, meter scale, and weight machine were used to collect the statistical data of the subjects. The anthropometric descriptions of the participants are shown in Table 1.

Table 1.

Description of anthropometric measurements.

Characteristics Mean S. D Range
Age (years) 24 5.48 18–28
Height (cm) 164 3.92 152–170
Weight (kg) 62 8.89 58–74
BMI 24.33 2.11 22–28
Knee height (cm) 52 5.43 48–58
Forearm length (cm) 45.8 1.78 43–48
Foot length (cm) 24.75 2.03 43–47
Years of rider 5 1.54 2.5–7.5
Open in a new tab

2.2. Vibration measurement

Subjects were asked to drive the motor bike with the speed of 20 Km/h in the standard speed humps (Height: 101 mm, Length: 152 mm, Wide: 355 mm). Vibration transmitted from the speed humps to the subjects’ buttock was measured using tri-axial accelerometer (Kistler, 8763), data acquisition system (DAQ with dynamic analyser, 9234) through a NI USB-9234 card to Core 2 duo processor based Lenovo laptop as shown in Fig. 1. Vibration levels along all directions (Xh_, Yh_ and Zh_) were measured using DEWESOFT software with the sampling rate of 1024 frames per second.

Fig. 1.

Fig. 1

Open in a new tab

Vibration measurement setup.

Light-weight strip was used to attach the accelerometer (2.4 g) in the bike seat according to ISO5349-2. In order to maintain the accuracy of the experiment, National Institute for Occupational Safety and Health (NIOSH), suggested that the total weight of the accelerometer and adopter be less than 20 g. The experiment was initiated once the subjects were in correct posture. Two trails were calculated for each subject to maintain the accuracy. Results were recorded to the spreadsheet and frequency-weighted RMS acceleration (ahwx, ahwy and ahwz) was calculated for each axis. The total value of average RMS vibration (ahv) was calculated for all the subjects.

2.3. Force calculation

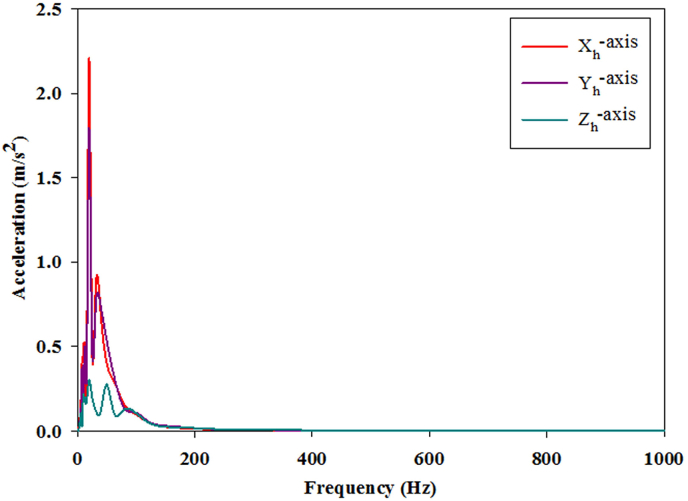
Fig. 2 shows the relationship between frequency and acceleration (frequency domain). From the frequency domain graph, the peak accelerations for x, y and z axes were found to be 2.2 m/s2, 1.7 m/s2 and 0.3 m/s2. The root mean square value was obtained as 1.65 m/s2 by considering the peak accelerations in Eqn. (1). Transmissibility factor was considered to be 0.5 at 10 Hz and 70 kg as mean weight of the subjects for force calculation. The input force for lumbar spine was calculated as 401.1 N using Eqn. (2).

R.M.S=xx2+xy2+xz2 (1)
InputForce=(TransmissibilityFactor+WeightoftheSubject+Acceleration)Acceleration=R.M.S+Accelerationduetogravity (2)

Fig. 2.

Fig. 2

Open in a new tab

Frequency domain graph.

2.4. L-4 lumber spine FE model

Nonlinear L-4 lumber spine three-dimensional (3D) FE model was developed using Computed Tomography (CT) scan from a healthy subject. Three-dimensional (3D) geometry of L-4 lumbar spine model was developed by importing the DICOM data obtained from CT scanning. Two dimensional (2D), CT scanning images were imported into MIMICS software with the slice thickness of 1.0 mm and converted into 3D point cloud data. Segmentation and 3D construction were performed by importing the 3D cloud data into SOLIDWORKS 2016. Threshold technique was considered in segmentation with threshold value of 200 for obtaining better segmentation. In order to identify segmentation errors, small inclusions, holes and ribs feature recognition technique was used. 3D reconstruction technique was performed for surface smoothening. The resulting 3D L-4 lumbar spine model was shown in Fig. 3.

Fig. 3.

Fig. 3

Open in a new tab

Three-dimensional (3D) lumbar spine (L-4) model.

2.5. Material properties

The material properties of L-4 lumbar spine were assumed to be isotropic and homogenous. The material properties used in the lumbar spine were adopted from the literature.21 The properties of cortical bone, cancellous bone and Posterior element are shown in Table 2. In the present study, linear hexahedron mesh and ten node quadratic tetrahedral (C3D10) elements type was considered for cortical bone, cancellous bone and posterior element. The FE model approximately included 346548 nodes and 156621 tetrahedral units. Mesh convergence test was conducted to find the suitable mesh resolution for the FE model to confirm the accurateness of the simulation. Sensitivity analysis was performed to estimate the material properties using least square fitting method. Static and dynamic analysis was performed in the FE model to identify the strain and magnitude between homogenous and heterogenous model. The mesh convergence test and sensitivity analysis results are in good agreement with the linearized model and nonlinear model.14 FE model was constrained along the spinal tract and the front face is loaded with the force calculated from the accelerometer readings.

Table 2.

Material properties of biological components used in lumbar spine (L-4) model.21

Tissue Property Applied Element Type
Cortical Bone Young's Modulus 1200 MPa Ten node quadratic tetrahedral (C3D10)
Density 1.91 g/cm3
Poission's Ratio 0.30
Cancellous Bone Young's Modulus 100 MPa Ten node quadratic tetrahedral (C3D10)
Density 1.87 g/cm3
Poission's Ratio 0.20
Posterior element Young's Modulus 3500 MPa Ten node quadratic tetrahedral (C3D10)
Density 1.87 g/cm3
Poission's Ratio 0.25
Open in a new tab

2.6. Simulation procedure

2.6.1. Static analysis

Three-dimensional finite element simulations were performed to evaluate the bio-mechanical behaviour of the L-4 lumber spine. In this study, input force (401.1 N) applied in the L-4 lumbar spine model and analysis was performed using quasi-static. The entire loading was accomplished over 100 incremental steps. Load parameterization analysis was performed to estimate the displacement of L-4 lumbar spine model. In load parameterization analysis load was varied from 400 N to 900 N as 5 incremental steps. The deformations on the FE model were calculated using static analysis and the computations were performed in time-domain.

2.6.2. Dynamic analysis

The dynamic simulation procedure was performed in two stages; (i) Mode based steady-state dynamic analysis, (ii) Steady-state dynamics during harmonic excitations. The mechanical responses of the L-4 lumbar spine model subjected to the continuous harmonic analysis are analysed using linear perturbation procedure. The L-4 lumbar spine model was actuated in the three-dimensional harmonic excitations with a velocity magnitude of 10 mm/s at a phase of 0°. The dynamic simulation was performed in the frequency range of 0–200 Hz. Steady state dynamic analysis, the dynamic responses of the finger were analysed in the frequency domain. The dynamic behaviour of the L-4 lumbar spine can be investigated during the frequency-dependent distributions.

3. Results and discussion

3.1. Quasi-static analysis

From the static analysis of the L-4 lumbar spine, the highest stress concentrations are around pedicle region and lamina areas (Fig. 4). This indicates that, in L-4 lumbar spine pedicle region and spinal canal areas have highest possibility for fracture. The von-Mises stress in the lumbar spine ranges from minimum of 5.59 E−07 N/m2 to the maximum of 2.16 E+01 N/m2. The stress distributions in the various regions are shown in Fig. 4 (see Fig. 5).

Fig. 4.

Fig. 4

Open in a new tab

Stress distributions on the lumbar spine.

Fig. 5.

Fig. 5

Open in a new tab

Various regions stress distribution on lumbar spine due to speed hump.

Quasi-static analysis results suggest that, pedicle region has the highest stress concentration of 2.5 E+01 N/m2 and followed by spinal canal, spinious, body, transverse process, anterior facet with stress concentration of 2.0 E+01 N/m2, 1.25 E+01 N/m2, 1.0 E+01 N/m2, 0.8 E+01 N/m2, 0.7 E+01 N/m2 respectively. The actual fracture starts from the junction between the pedicle and the spinal canal. The transverse process and anterior facet experience a small amount of load as shown in Fig. 4. Furthermore, the results of the lumbar spine stress in the current FE model predicted the same trends with the study of Rohlmann et al.22

The region between pedicle and spinal canal are selected as an area of interest as it experiences highest stress and further analysis are performed by selecting a node at that region where maximum stress occurs. Graphical analysis of the pedicle and spinal region is shown in Fig. 6. The stress tends to increase along the boundary between the pedicles and the spinal canal where the stress reaches the maximum value. The stress distribution between the pedicle and spinal canal region is shown in Fig. 7. The results suggest that, Node 3 (2.51 E+01 N/m2) and Node 4 (2.49 E+01 N/m2) have the highest level of stress concentration, Node 2 (2.08 E+01 N/m2) and Node 5 (2.1 E+01 N/m2) have the medium level of stress concentration (2.0 E+01 N/m2) and Node 1 (1.78 E+01 N/m2) and Node 6 (1.91 E+01 N/m2) have less stress concentration in the pedicle and spinal canal region. The results predicted from the present study are in good agreement with the range of the experiments.23

Fig. 6.

Fig. 6

Open in a new tab

Graphical analysis of the pedicle spinal canal region.

Fig. 7.

Fig. 7

Open in a new tab

Node based stress distribution of lumbar spine.

The load parameterization results are shown in Fig. 8. The results suggest that, at a load of 400 N the stress was found to be around 25 MPa. The stress level varies gradually at 500 N and found to be around 42 MPa. The maximum stress was attained in the load parameterization analysis was 87 MPa at 900 N. The breaking stress of the L-4 lumbar spine bone around 82 MPa was calculated by the experimental study occurred at 870 N. Therefore, a load of 870 N and above will cause failure of the L-4 lumbar spine bone. The simulation result of maximal compressive strain is shown in Fig. 9. From the static analysis compressive strain was found to be 0.0025. The maximum strain was distributed through the pedicle, spinal canal, spinious body, transverse process, and anterior facet. Compressive strain results suggest that lamina region have less strain value compared to the other regions. The static analysis result also suggests that for the entire loading condition maximum displacement magnitude was found to be 0.0026 m. The maximum displacement magnitude was found in transverse process and in articular facet as shown in Fig. 10. Spinous process and body region produce less displacement due to additional amount of thickness in that region. The findings of the present study are consistent with previous research results reported.24

Fig. 8.

Fig. 8

Open in a new tab

Load parameterization stress distribution.

Fig. 9.

Fig. 9

Open in a new tab

Maximal compressive strain distributions on lumbar spine.

Fig. 10.

Fig. 10

Open in a new tab

Displacement magnitude of lumbar spine.

3.2. Dynamic analysis

3.2.1. Mode based steady-state dynamic analysis

The frequency dependent vibration magnitude distribution was estimated using the modal analysis. From the dynamic point of view, modal analysis results suggest the resonant frequencies of the L-4 lumbar spine model. The vibration mode response of the L-4 lumbar spine model is shown in Fig. 11. The vibration displacement magnitude was found maximum of 0.7 mm at 18 Hz and minimum of 0.28 mm at 8 Hz. The displacement magnitude was found to be 0.42 mm and 0.57 mm at 31 Hz and 40 Hz respectively. The mode frequencies obtained from this study is consistent with previous research reported with dynamic motion of in-vivo L4-5 lumbar disc.25

Fig. 11.

Fig. 11

Open in a new tab

Mode based displacement of lumbar spine, (a) Displacement at 8 Hz, (b) Displacement at 18 Hz, (c) Displacement at 31 Hz, (d) Displacement at 40 Hz.

3.2.2. Steady-state dynamics during harmonic excitations

The L-4 lumbar spine FE model was subjected to the harmonic excitation in order to estimate the dynamic response and to understand the behaviour of the model with respect to the frequency. The outcome of the dynamic analysis was estimated as a result of stress, displacement, velocity and acceleration with respect to the frequency as shown in Fig. 12. The simulation result suggests that the stress was found maximum of 443 MPa at the resonance frequency at 18 Hz. At peak frequency of 31 Hz the stress was found to be 183 MPa. Fig. 12(b) shows that the displacement was found to be the maximum of 0.065 m and 0.018 m at 18 Hz and 31 Hz, respectively. From Fig. 12(c), it was inferred that maximum velocity of 0.0075 m/s and 0.003 m/s was found at frequency of 18 Hz and 31 Hz, respectively. Fig. 12(d), shows the first peak acceleration of 0.78 m/s2 occurs at 18 Hz and second peak acceleration of 0.36 m/s2 occurs at 31 Hz. The stress, displacement, velocity, and acceleration value declines beyond 40 Hz as the frequency increases. The dynamic results obtained in the present work are in accordance with the previous study results based on dynamic stability of lumbar spine.26

Fig. 12.

Fig. 12

Open in a new tab

Dynamic response of the lumbar spine (a) Frequency Vs Stress, (b) Frequency Vs Displacement, (c) Frequency Vs Velocity, (d) Frequency Vs Acceleration.

4. Discussion

The biomechanical behaviour of lumbar spine while riding on the speed hump was evaluated using static and dynamic analysis. The static analysis results suggest that highest stress was found in the pedicle and spinal canal region because of the speed hump. The structure of the pedicle and spinal canal is also another reason for the highest stress concentration. Pedicle region have small thickness and spinal canal have sharp corner regions than the lumbar spine body to which they are attached also leads to higher stresses. The prevalent regions for injuries due to loading are around pedicle and spinal canal due to high stress concentrations. Impact or large loads which can result to acute stress fractures in the particular regions. Goel et al.27 investigated the effect of load sharing, different moments between posterior rods and an artificial disc the results are in good agreement with the present study. Experimental and simulation were performed to measure the strain on the vertebral body and facet lateral mass under different loading conditions. The results are in good agreement across the range of force applied on the vertebral body and facet lateral mass. Dynamic finite element vertebral model displacements across the disc were identified using high speed video and the results are predicted with good agreement.28

The dynamic analysis results gave the clear structure of the frequency response with respective of lumbar spine mode shapes. The resonant frequencies of the L-4 lumbar spine model can be viewed as vibration modes in various regions. The simulation results indicated the major resonance of the L-4 lumbar spine model is around 8–40 Hz. The simulation results suggested that the symmetric distribution of vibration magnitude was found in the pedicle, spinal canal, body, transverse process, anterior facet, and unsymmetrical distribution of vibration magnitude was found in spinious process. The stress, displacement, velocity, and acceleration value declines beyond 40 Hz as the frequency increases. The simulation results indicate that below 40 Hz the lumbar spine has more biomechanical response. Thus, finite element model represents the approximate response of bone model from real life conditions. However, the limitations of this study were only considering lumbar spine (L-4) model for finite element analysis. The future study will be evaluated by considering the entire vertebra, using finite element analysis to identify the risk level of while riding in the speed hump.

5. Conclusion

The influence of input force transmitted while riding in the speed hump has been assessed in this research. Three-dimensional lumbar spine (L-4) was reconstructed from the CT scan data and finite element analysis was performed. The study demonstrates the biomechanical behaviour of lumbar spine during static and dynamic analyses. The following conclusions drawn from the studies are.

  • •

    The input force transmitted to the lumbar spine while riding the motorbike in the speed hump at 20 km/h was found to be 401.1 N.

  • •

    Quasi-static analysis results suggest that highest stress concentration was found in the pedicle and lamina areas which lead to fracture during the large loading or impact loading conditions.

  • •

    The vibration magnitude was found maximum during the natural frequencies of the lumbar spine. The mode frequencies are found to be 8 Hz, 18 Hz, 31 Hz and 40 Hz.

  • •

    The stress, displacement, velocity, and acceleration were distributed maximum during 18 Hz and 31 Hz.

  • •

    The study results have certain reference values which are useful for researchers for future development and to understand the biomechanical behaviour of lumbar spine.

CRediT authorship contribution statement

B. Jain A R Tony: Conceptualization, Methodology, Formal analysis, Writing - original draft. M.S. Alphin: Supervision, Validation, Visualization, Writing - review & editing. G. Sri Krishnan: Data curation, Software.

Declaration of competing interest

Authors declare no conflict of interest for the submitted manuscript.

References

  • 1.Balasubramanian V., Jagannath M. Detecting motorcycle rider local physical fatigue and discomfort using surface electromyography and seat interface pressure. Transport Res Part F. 2014 Jan;22:150–158. [Google Scholar]
  • 2.Walker G.H., Stanton N.A., Young M.S. The ironies of 262 vehicle feedback in car design. Ergonomics. 2006 Feb 10;49(2):161–179. doi: 10.1080/00140130500448085. [DOI] [PubMed] [Google Scholar]
  • 3.Alperovitch-Najenson D., Katz-Leurer M., Santo Y., Golman D., Kalichman L. Upper body quadrant pain in bus drivers. Arch Environ Occup Health. 2010 Nov 06;65(4):218–223. doi: 10.1080/19338244.2010.486422. [DOI] [PubMed] [Google Scholar]
  • 4.Thamsuwan O., Blood R.P., Ching R.P., Boyle L., Johnson P.W. Whole body vibration exposures in bus drivers: a comparison between a high-floor coach and a low-floor city bus. Int J Industr Ergonom. 2013 Jan;43(1):9–17. [Google Scholar]
  • 5.Okunribido O.O., Shimbles S.J., Magnusson M., Pope M. City bus driving and low back pain: a study of the exposures to posture demands, manual materials handling and wholebody vibration. Appl Ergon. 2007 Jan;38(1):29–38. doi: 10.1016/j.apergo.2006.01.006. [DOI] [PubMed] [Google Scholar]
  • 6.Niemeyer F., Wilke H.J., Schmidt H. Geometry strongly influences the response of numerical models of the lumbar spine-A probabilistic finite element analysis. J Biomech. 2012 Mar;45(8):1414–1423. doi: 10.1016/j.jbiomech.2012.02.021. [DOI] [PubMed] [Google Scholar]
  • 7.Schmidt H., Bashkuev M., Dreischarf M. Computational biomechanics of a lumbar motion segment in pure and combined shear loads. J Biomech. 2013 Sep 27;46(14):2513–2521. doi: 10.1016/j.jbiomech.2013.06.038. [DOI] [PubMed] [Google Scholar]
  • 8.Kiapour A., Anderson D., Spenciner D., Ferrara I., Goel V. Kinematic effects of a pedicle lengthening osteotomy for the treatment of lumbar spinal stenosis. J Neurosurg Spine. 2012 Oct;17(4):314–320. doi: 10.3171/2012.6.SPINE11518. [DOI] [PubMed] [Google Scholar]
  • 9.Dreischarf M., Zander T., Bergmann G., Rohlmann A. A non-optimized follower load path may cause considerable intervertebral rotations. J Biomech. 2010 Sep 17;43(13):2625–2628. doi: 10.1016/j.jbiomech.2010.05.033. [DOI] [PubMed] [Google Scholar]
  • 10.Little J., Adam C. Geometric sensitivity of patient-specific finite element models of the spine to variability in user selected anatomical landmarks. Comput Methods Biomech Biomed Eng. 2013 Nov 21;18(6):676–688. doi: 10.1080/10255842.2013.843673. [DOI] [PubMed] [Google Scholar]
  • 11.Stokes I.A.F. Proceedings of the first International workshop on the contribution of biomechanics to the prevention and treatment of low back pain. Clin Biomech. 1997;12:195–197. doi: 10.1016/s0268-0033(97)00064-8. [DOI] [PubMed] [Google Scholar]
  • 12.Adams M.A., Dolan P. Recent advances in lumbar spinal mechanics and their clinical significance. Clin Biomech. 1995 Jan;10(1):3–19. doi: 10.1016/0268-0033(95)90432-9. [DOI] [PubMed] [Google Scholar]
  • 13.Sawa A., Crawford N. The use of surface strain data and a neural networks solution method to determine lumbar facet joint loads during in vitro spine testing. J Biomech. 2008 Aug 28;41(12):2647–2653. doi: 10.1016/j.jbiomech.2008.06.010. [DOI] [PubMed] [Google Scholar]
  • 14.Ayturk U., Puttlitz C. Parametric convergence sensitivity and validation of a finite element model of the human lumbar spine. Comput Methods Biomech Biomed Eng. 2011 Aug;14(8):695–705. doi: 10.1080/10255842.2010.493517. [DOI] [PubMed] [Google Scholar]
  • 15.Kiapour A., Ambati D., Hoy R.W., Goel V. Effect of graded facetectomy on biomechanics of Dynesys dynamic stabilization system. Spine. 2012 May 1;37(10):581–589. doi: 10.1097/BRS.0b013e3182463775. [DOI] [PubMed] [Google Scholar]
  • 16.Lin H., Pan Y., Liu C., Huang L., Huang C., Chen C. Biomechanical comparison of the K ROD and Dynesys dynamic spinal spinal fixator systems – a finite element analysis. Bio Med Mater Eng. 2013 Oct;23(6):495–505. doi: 10.3233/BME-130766. [DOI] [PubMed] [Google Scholar]
  • 17.Zander T., Rohlmann A., Bergmann G. Influence of different artificial disc kinematics on spine biomechanics. Clin Biomech. 2009 Feb;24(2):135–142. doi: 10.1016/j.clinbiomech.2008.11.008. [DOI] [PubMed] [Google Scholar]
  • 18.Schmidt H., Galbusera F., Rohlmann A., Zander T., Wilke H. Effect of multilevel lumbar disc arthroplasty on spine kinematics and facet joint loads in flexion and extension: a finite element analysis. Eur Spine J. 2012 Jun;21(S5):663–674. doi: 10.1007/s00586-010-1382-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Shirazi-Adl A. Analysis of role of bone compliance on mechanics of a lumbar motion segment. J Biomech Eng. 1994 Nov;116(4):408–412. doi: 10.1115/1.2895791. [DOI] [PubMed] [Google Scholar]
  • 20.Park W., Kim K., Kim Y. Effects of degenerated intervertebral discs on intersegmental rotations, intradiscal pressures, and facet joint forces of the whole lumbar spine. Comput Biol Med. 2013 Sep;43(9):1234–1240. doi: 10.1016/j.compbiomed.2013.06.011. [DOI] [PubMed] [Google Scholar]
  • 21.Ming Xua, Yang James, Lieberman Isador H., Ram Haddas. Lumbar spine finite element model for healthy subjects: development and validation. Comput Method Biomec. 2017 Jan;20(1):1–15. doi: 10.1080/10255842.2016.1193596. [DOI] [PubMed] [Google Scholar]
  • 22.Rohlmann A., Zander T., Schmidt H., Wilke H., Bergmann G. Analysis of the influence of disc degeneration on the mechanical behaviour of a lumbar motion segment using the finite element method. J Biomech. 2006 Sep 29;39(13):2484–2490. doi: 10.1016/j.jbiomech.2005.07.026. [DOI] [PubMed] [Google Scholar]
  • 23.Hayes M.A., Howard T.C., Gruel C.R., Kopta J.A. Roentgenographic evaluation of lumbar spine flexion-extension in asymptomatic individuals. Spine. 1989 Mar;14(3):327–331. doi: 10.1097/00007632-198903000-00014. [DOI] [PubMed] [Google Scholar]
  • 24.Jones D.A., Gaewsky J.P., Kelley M.E., Weaver A.A., Miller A.N., Stitzel J.D. Lumbar vertebrae fracture injury risk in finite element reconstruction of CIREN and NASS frontal motor vehicle crashes. J Crash Prev Inj Control. 2016;17(sup1):109–115. doi: 10.1080/15389588.2016.1195495. [DOI] [PubMed] [Google Scholar]
  • 25.Tao Nie1, Chen De-jian, Tang Benyu. In vivo dynamic motion characteristics of the lower lumbar spine: L4–5 lumbar degenerative disc diseases undergoing unilateral or bilateral pedicle screw fixation combined with TLIF. J Orthop Surg Res. 2019 Jun 26;14(1):171. doi: 10.1186/s13018-019-1198-6. 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Zhang C., Wang L., Hou T. The influence of L4-S1 Dynesys® dynamic stabilization versus fusion on lumbar motion and its relationship with lumbar degeneration: a retrospective study. J Orthop Surg Res. 2017 Jun 26;12(1):99. doi: 10.1186/s13018-017-0597-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Goel V.K., Grauer J.N., Patel T.C. Effects of charite artificial disc on the implanted and adjacent spinal segments mechanics using a hybrid testing protocol. Spine. 2005 Dec 15;30(24):2755–2764. doi: 10.1097/01.brs.0000195897.17277.67. [DOI] [PubMed] [Google Scholar]
  • 28.Wilcox R.K., Allen D.J., Hall R.M., Limb D., Barton D.C., Dickson R.A. A dynamic investigation of the burst fracture process using a combined experimental and finite element approach. Eur Spine J. 2004 Oct;13(6):481–488. doi: 10.1007/s00586-003-0625-9. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Journal of Orthopaedics are provided here courtesy of Elsevier

RESOURCES