Figure 3. Linear System Model Predicts the Responses to Single Pulses.

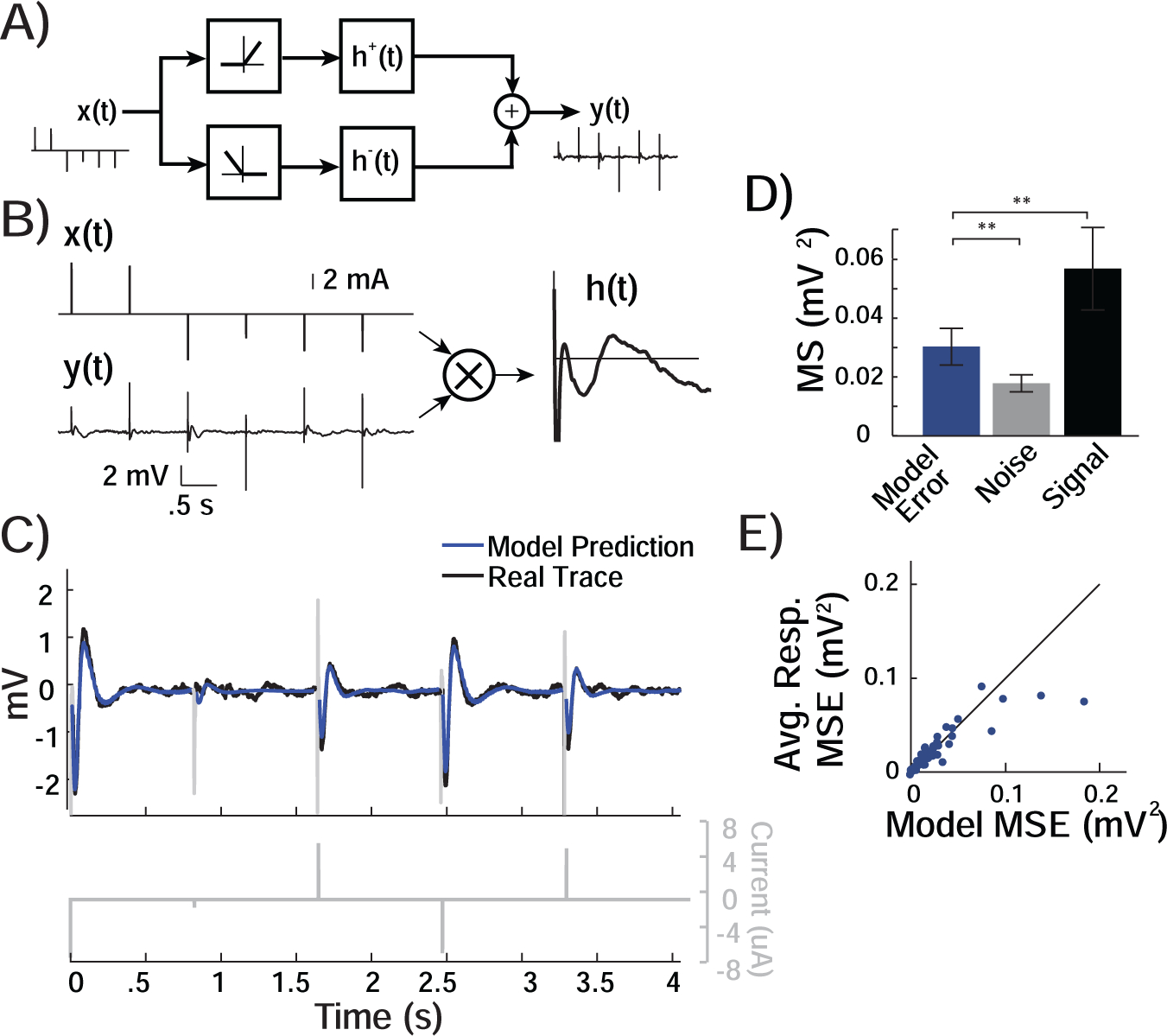
A) When constructing the simple model characterizing the response to stimulation, we divided each training series of pulses, x[t], into positive and negative pulses because the responses to stimulation appeared symmetric. We therefore modeled the system as a nonlinear rectification followed by a separate impulse response, h⁺[t] and h⁻[t] for positive and negative pulses, that together produce the output y[t]. B) Cross-correlating the input x[t] of stimulation pulses with the recorded output, y[t], generates the first order kernel, or impulse response h[t], of the system for each recorded electrode. C) For each recorded electrode, we can convolve any new input x[t] with the derived model to generate a prediction, ŷ[t] of the evoked response. The model prediction appears to match the actual evoked response, y[t], to the novel series of pulses. D) Across responsive electrodes, the MSE between the predicted and recorded response (Model Error) was significantly lower than the mean of squares of the signal, which is equivalent to the MSE if the predicted response were the mean value of zero, (MS_signal, Signal). The residual error was higher than the mean of squares of the baseline activity, which is the lowest possible level of MSE that is attainable (MS_noise, Noise). The model prediction reduced the error from its maximum value to its minimum possible value by 69.7 ± 12.1% across responsive electrodes. **, p < .01; paired t-test. E) The MSE for each responsive electrode using the model prediction was similar to the MSE derived using the prediction based on the average response. Each point represents a single responsive electrode.