Figure 2.

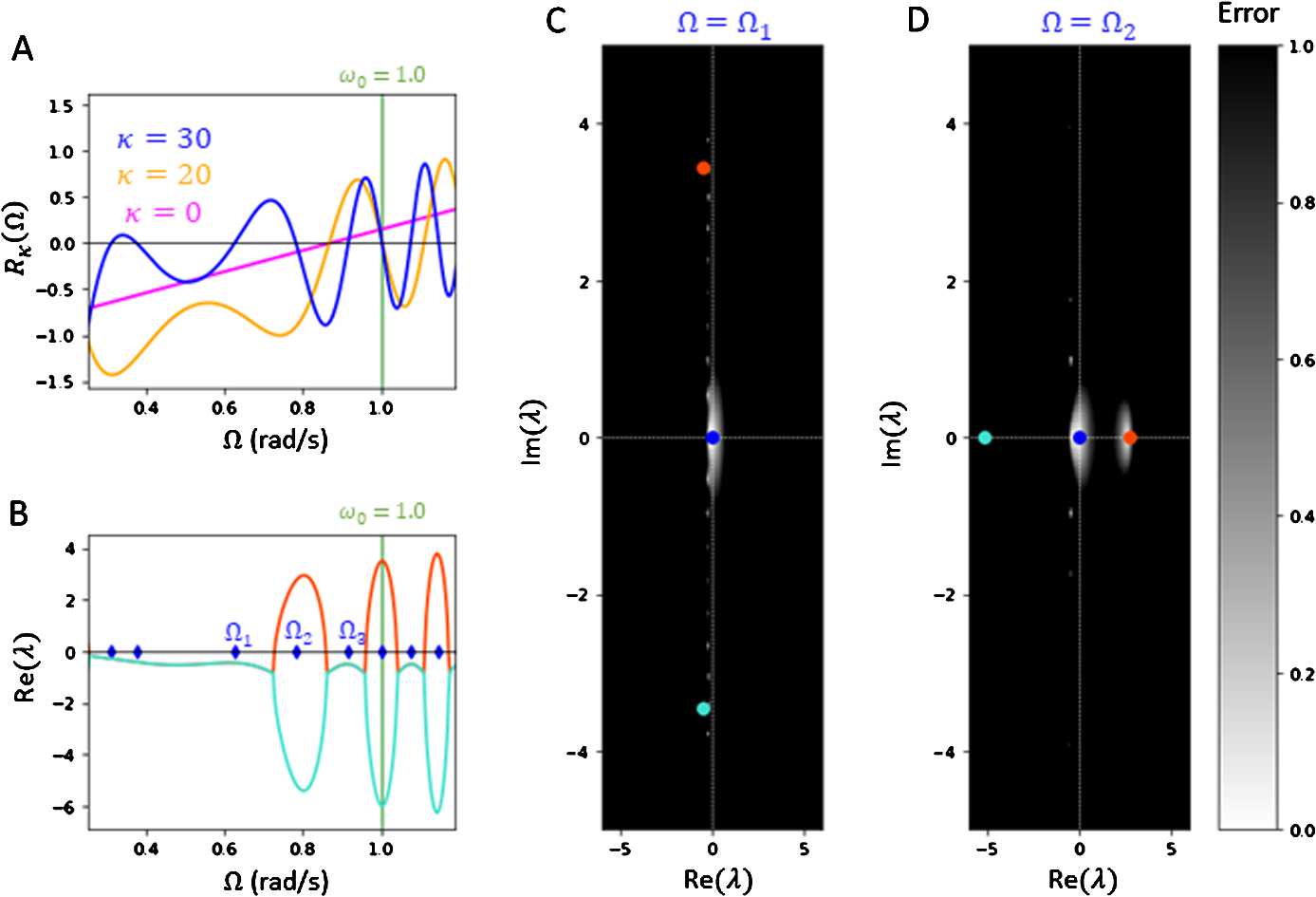
Theoretical stability plots for two-oscillator system. A. Plot of error functions $R_{\kappa }(\Omega )$ with varying fixed gain $\kappa =0$ (magenta), $\kappa =20$ (yellow), $\kappa =30$ (blue). All roots $\Omega \in [{\omega }_0-g,{\omega }_0)$ of $R_{\kappa }(\Omega )$ are potential synchronization frequencies for the two-oscillator system. The number of roots Ω for ${\mathcal{R}}_{\kappa }(\Omega )=0$ increase with larger κ. B. The plasticity gain is set to $\kappa =30$. Plot of the real part of the non-zero branches ${\lambda }_1(\Omega )$, ${\lambda }_2(\Omega )$ (orange, cyan) of the polynomial root equation $P_{\Omega }(\lambda )+Q_{\Omega }(\lambda )=0$ over $\Omega \in [{\omega }_0-g,{\omega }_0)$. Ticks on the Ω-axis (blue) indicate the frequencies ${\Omega }_i$ solving ${\mathcal{R}}_{\kappa }({\Omega }_i)=0$ where the system can synchronize. The plotted branches imply that the oscillators will synchronize at $\Omega ={\Omega }_1,{\Omega }_3$, and avoid the unstable frequency $\Omega ={\Omega }_2$ with $Re{\lambda }_1({\Omega }_2)>0$. C, D. Error heatmaps with $\Omega ={\Omega }_1,{\Omega }_2$, respectively, approximate the distribution of eigenvalues $\lambda \in \mathbb{C}$ solving $P_{\Omega }(\lambda )+Q_{\Omega }(\lambda )e^{-\lambda \tau }=0$ near $\lambda =0$, scaled and normalized for visibility. Spots near zero error (white) suggest potential eigenvalue locations. Markers plot the eigenvalues ${\lambda }_0=0,{\lambda }_1(\Omega ),{\lambda }_2(\Omega )$ (blue, orange, cyan) for $\tau =0$. The heatmap in D indicates an eigenvalue λ near ${\lambda }_1({\Omega }_2)>0$, which implies instability at $\Omega ={\Omega }_2$. All other eigenvalues λ appear to be distributed either at $\lambda =0$ or on the left-side of the imaginary axis. Here, ${\Omega }_1=0.626$ and ${\Omega }_2=0.783$. For all plots, ${\alpha }_{\tau }=0.5$, $g=1.5/2$, ${\omega }_0=1.0$, $\kappa =30$, and ${\tau }^0=0.1\text{s}$