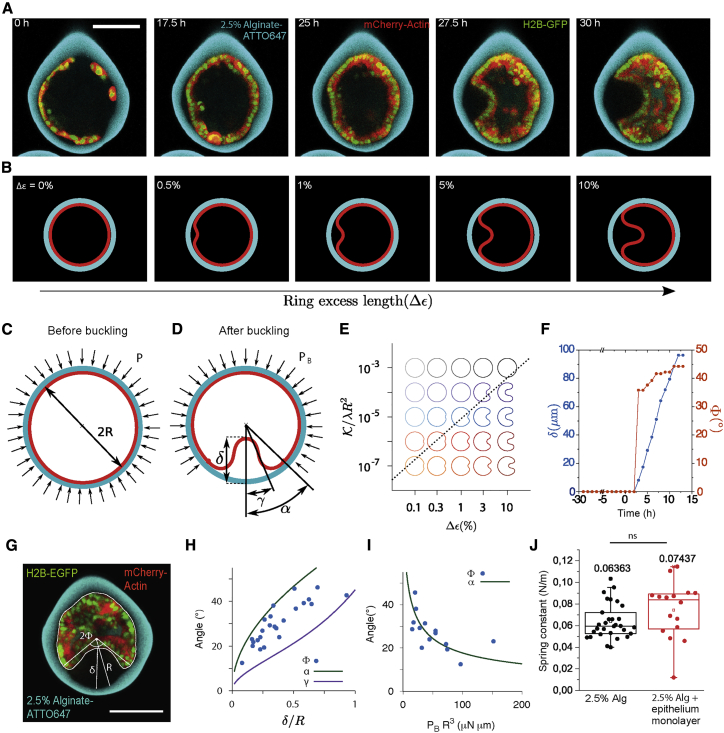
Figure 4.

Continuum Theory of the Buckling Transition and Comparison to Experimental Data

(A) Confocal equatorial planes of epithelial monolayer bending.

(B) Equilibrium shapes of a buckled elastic ring (red) under circular confinement (cyan) as a function of ring excess strain (Δε), calculated from continuum theory (see Figure 4B and Supplemental Information).(C) Schematic of a compressed elastic ring (red) under the pressure P of the confinement ring (cyan). (D) Schematic of a buckled elastic ring (red) under the pressure P_B of the confinement ring (cyan).

(E) Equilibrium shapes as a function of K /λR² and the excess strain Δε. The dashed line stands for the threshold given by Equation S25 in Method S1. List of parameters: K = 10⁻², k = 10⁵, R = 1, and λ varies from 10 to 10⁵.

(F) Experimental values of δ (n = 43 from 3 replicates) and Φ (n = 43 from 3 replicates) as a function of time. Time point 0 corresponds to the monolayer confluence.

(G) Experimental measurements of δ, Φ, R depicted on a confocal equatorial scan of a capsule with a buckled monolayer.

(H) Blue dots, experimental values of (Φ;δ), (n = 24, from 3 replicates). Solid lines; theoretical relations between δ and α (green) and δ and γ (purple) for the compressional rigidity 10 8.

(I) Blue dots, experimental values (Φ,P_B R³), n = 14, from (F). Only dots where δ was smaller than R were kept for the fit. Solid green line fits to the theoretical relation between α and P_BR³ giving K = 0.5 μN.μm.

(J) Spring constant values of 2.5% alginate capsules with (n = 17 from 2 replicates) and without (n = 31 from 3 replicates) a cell monolayer (see Figure S5). The difference is not statistically significant with two-tailed p value 0.5809.