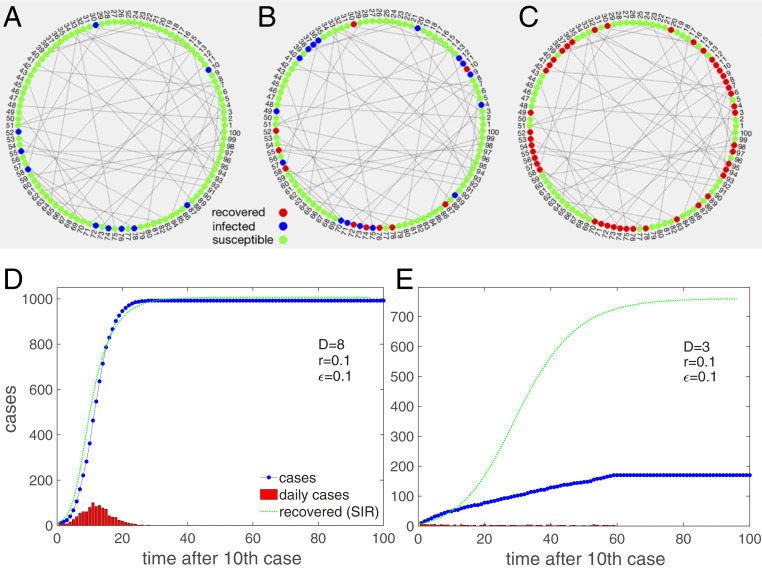
Fig. 2.

Schematic demonstration of the model. Nodes are connected in a Poissonian small-world network. Locally close neighbors resemble the family contacts, and long links to different regions represent contacts to others, such as people at work. (A) Initially, a subset of nodes is infected (blue), and most are susceptible (green). (B) At every timestep, infected nodes spread the disease to any of their neighbors with probability $r$. After $d$ days infected nodes turn into “recovered” and no longer spread the disease. (C) The dynamics end when no more nodes can be infected and all are recovered. (D) Infection curve $P\left(t\right)$ (blue dots) for the model on a dense Poissonian small-world network, $D=8$. The daily cases (red) first increase and then decrease. For comparison, we show the recovered cases, $R\left(t\right)$, of the corresponding SIR model with $\gamma =1/d$, and $\beta =rD/N$ (green). The mean-field conditions are obviously justified to a large extent. (E) Situation for the same parameters except for a lower average degree, $D=3$. The infection curve now increases almost linearly; daily increases are nearly constant for a long time. The dynamics reach a halt at about 17% infected. The discrepancy to the SIR model (green) is now obvious.