Abstract
In this manuscript, we solve a model of the novel coronavirus (COVID-19) epidemic by using Corrector-predictor scheme. For the considered system exemplifying the model of COVID-19, the solution is established within the frame of the new generalized Caputo type fractional derivative. The existence and uniqueness analysis of the given initial value problem are established by the help of some important fixed point theorems like Schauder’s second and Weissinger’s theorems. Arzela-Ascoli theorem and property of equicontinuity are also used to prove the existence of unique solution. A new analysis with the considered epidemic COVID-19 model is effectuated. Obtained results are described using figures which show the behaviour of the classes of projected model. The results show that the used scheme is highly emphatic and easy to implementation for the system of non-linear equations. The present study can confirm the applicability of the new generalized Caputo type fractional operator to mathematical epidemiology or real-world problems. The stability analysis of the projected scheme is given by the help of some important lemma or results.
Keywords: COVID-19, Mathematical model, New generalized Caputo-type fractional derivative, Predictor-corrector algorithm, Fixed point theorems
MSC: 26A33, 34C60, 92C60, 92D30
1. Introduction
In December 2019, a new atypical pneumonia caused by a virus called Corona Virus (COVID-19) was appeared in China in the city of Wuhan [16], [20], [28]. From the date of its origin it exponentially growths in the mankind and infected more than 12,925,331 with 569,097 deaths and 7,529,774 recoveries on July 12 throughout the globe. In particularly, United States is one of the most infected country of this virus with 3,381,274 cases, 137,577 deaths and 1,501,866 recoveries. Brazil and India are also in this list where the COVID-19 cases are increasing rapidly day by day. The symptoms of this virus include coughing, breathing difficulties, and fever. It is well known that the transmission of the virus from human to human but still there are some specific cases where this virus has been recognised in animals also. There are a lot of research articles have been come in literature to analyse the effects of COVID-19 via mathematical modelling. Particularly, analysis of unreported cases of COVID-19 in Wuhan, China has been done in Khoshnaw et al. [9], Liu et al. [14] and restudied by using q-homotopy analysis transform method in Gao et al. [5], predictions of coronavirus peaks in Japan given in Kuniya [11] and one of the brief study of details of interaction among the bats and unknown hosts, then among the peoples and the infections reservoir via fractional derivatives observed in Khan and Atangana [8]. Abdo et al. [1], discussed a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative. Lots of coronavirus updates can be found from [26]. A study entitled ‘Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS’ given in Liang [13] and ‘Short-term predictions and prevention strategies for COVID-2019: A model based study’ can be recognised in Nadim et al. [17]. Non-linear systems are useful to study the complex dynamics. An investigation to the issue of fuzzy adaptive control for a class of strict-feedback nonlinear systems with non-affine nonlinear faults is discussed in Sun et al. [24]. A study on event-triggered robust fuzzy adaptive finite-time control of nonlinear systems with prescribed performance is discussed in Sun et al. [23]. In [25], a novel finite-time control for non-strict feedback saturated non-linear systems with tracking error constraint is investigated.
Integer order calculus is a well known theory for researchers and its limitations too, specifically while analysing the phenomena associated to diffusion, hereditary properties, long-range wave, history-based phenomena and others. The theory of fractional calculus is more then 300 years old and nowadays this is a important phenomena to fulfil the requirements in the study of real world problems. There are so many fractional derivatives have been introduced in the literature of fractional calculus in which Caputo, Caputo–Fabrizio and Atangana–Baleanu are the most commonly used derivatives in the various fields. In the present study we are analysing the results by the help of a newly proposed derivative called generalized Caputo derivatives which has the property similar to Caputo derivative [18]. There are a lot of research studies have been done by the help of fractional order derivatives and currently mathematical epidemiology is one of the town of fractional derivatives. Several non- integer order derivative models, where non-locality plays a very important role, in different fields, including engineering, physics, signal and image processing, mechanics and dynamical systems, biology, control theory and environmental sciences, have been introduced [6], [10], [15], [19], [21], [22], [27]. So many physical problems have been mobilised by the help of the Caputo fractional derivative in fractional calculus applications because Caputo derivative is suitable for initial value problems (IVPs) and has many characteristics similar to integer order derivatives. An study on overall behaviour of Maxwell mechanical model by the combined Caputo fractional derivative is presented in Feng et al. [4]. The nature of the generalised Caputo type fractional derivative also has the properties same as Caputo derivative. The predictor-corrector (P–C) scheme is one of the most efficient, stable and accurate scheme to solve the fractional initial value problem. In the current study we are using the modified P–C scheme to solve the projected model. The adaptive P–C algorithm in the sense of generalised Caputo sense uses a non uniform grid which is different from Caputo derivative P–C scheme. The generalized fractional integral operator is greatly influenced by the value of the parameters α and ρ, thus it gives a valuable tool to control and build mathematical models in fractional calculus applications. As compare to the other fractional derivatives like Caputo, Caputo–Fabrizio and Atangana–Baleanu, new generalised Caputo type fractional derivative has the extra features. Along with the fractional order parameter α, there is a one more parameter ρ which is very useful in the graphical simulations with respect to the true data. We can observe more varieties of graphs by the change of in the parameter value ρ. The structure of the real data of COVID-19 for different countries is not uniform with respect to time. So to study the nature of the classes of COVID-19 models more accurately by ordinary derivatives is difficult and in that situation the fractional derivatives are nice tools to study these data much clearly.
The aim of this paper is to find the solution of a COVID-19 model studied by Khoshnaw et al. [9] by the help of a new generalized Caputo fractional derivative with corrector- predictor algorithm. The main contribution of this paper is to study the nature of the given classes of model at different fractional order values with the uses of extra parameter ρ. The paper is formulated as follows. In Section 2, we recall some important results about generalised fractional derivatives in the literature of fractional calculus. Section 3 is devoted for the description of the ODE model following by the a fractional order model. Existence and uniqueness analysis of the problem are performed in Section 4. Solution of the projected model following stability analysis is done in Section 5. Simulation results are performed in Section 6. A conclusion completes the paper.
2. Preliminaries
Here, we remind some basic definitions and results about well known fractional derivatives and for new generalized Caputo-type fractional derivative.
Definition 1
Podlubny [21] The Caputo non- integer order derivative of is presented as
(1)
Definition 2 Caputo and Fabrizio [3] —
For g ∈ H 1(c, d) and the Caputo–Fabrizio (CF) fractional derivative(FD) of order η is defined by
(2) where and normalization function M(η) is such that
Definition 3 Atangana and Baleanu [2] —
For a function f ∈ H 1(c, d), where d > c and 0 ≤ γ ≤ 1, the fractional Atangana–Baleanu (AB) derivative (in Caputo sense) is expressed as follows:
(3)
Definition 4 Katugampola [7] —
The generalized Riemann-type fractional derivative operator, of order α > 0 is expressed as:
(4) where
Definition 5 Katugampola [7] —
The generalized Caputo-type fractional derivative operator, of order α > 0 is expressed as:
(5) where
Definition 6 Odibat and Baleanu [18] —
The new generalized Caputo-type fractional derivative operator, of order α > 0 is expressed as:
(6) where
Lemma 1 Li and Zeng [12] —
If 0 < β < 1 and m is an integer (nonnegative), then there exists the positive constants C β,1 and C β,2 only dependent on β, s.t
and
Lemma 2 Li and Zeng [12] —
Let us assumefor p ≥ n, β, M, h, T > 0, mh ≤ T m is a positive integer. Let for k > n ≥ 1. If
then
where C is a positive constant independent of m h.
3. Model description
In this portion, we express the model studied by Khoshnaw et al. [9] to introduce the COVID-19 epidemic in China. The considered model consists of five compartments with individuals of susceptible S(t), asymptomatic infectious I(t), unreported symptomatic infectious U(t), reported symptomatic infectious W(t) and recovered R(t). The author presented and derived the projected model in the sense of ordinary derivative as:
| (7) |
Now the generalisation of the projected system (7) in the new generalized Caputo-type fractional derivative as follows:
| (8) |
Let us write the system (8) in the compact form for easy description as follows:
| (9) |
with the initial conditions
4. Existence and uniqueness analysis
In this section, we give the existence of unique solution of the projected model by the help of the consequences of fixed point theory. we show the analysis for S(t) and for others it is similar. Let us consider the initial value problem (IVP)
| (10a) |
| (10b) |
The corresponding Volterra integral equation of above IVP is
| (11) |
Now, for the existence of solution we are proceeding with following results.
Theorem 1
(Existence). Letand T* > 0. Define and let the function be continuous. Further, define and
(12) Then, there exists a function S ∈ C[0, T] that solves the IVP (10a) and (10b) .
Lemma 3 Katugampola [7] —
Assume the hypotheses of Theorem1. The function S ∈ C[0, T] is a solution of the IVP (10a) and (10b) if and only if, it is a solution of the nonlinear Volterra integral Eq. (11) .
Proof
(Proof of Theorem 1) If then In this case it is clear by direct substitution that the function with is a solution of the IVP. Hence a solution exists in this case.
For M ≠ 0, we apply Lemma (3) and prove that IVP (10a) and (10b) is equivalent to the Volterra integral Eq. (11). Define the set It is clear that U is a closed and convex subset of the Banach space of all continuous functions on [0, T], equipped with the Chebyshev norm. Hence, U is a Banach space. U is non empty, since S 0 ∈ U. We define the operator E on this set U by
(13) Then, the Volterra Eq. (11) can be written as and thus, we have to show that E has a fixed point. This is done by the Schauders Second Fixed Point Theorem. We first show that U is closed, that is, ES ∈ U for S ∈ U. We begin by noting that, for 0 ≤ t 1 ≤ t 2 ≤ T,
The second integral in the right-hand side of the last inequality has the value For the first integral, consider the two cases separately. In the case the integral has the value zero. For α < 1, we have Thus,
Combining these results, we have
(14) if α ≤ 1. In either case, the expression on the right-hand side of (14) converges to 0 as t 2 → t 1, which proves that ES is a continuous function, since S(0) itself is continuous. It is also true that for S ∈ U and t ∈ [0, T],
(15) by the definition of T. Thus, we have ES ∈ U if S ∈ U, i.e. A maps the set U into itself. We only left to show that E(U) ≔ {Eu: u ∈ U} is relatively compact. This is done by the use of Arzel‘a-Ascoli Theorem. To show that the set E(U) is uniformly bounded, let z ∈ E(U). We see that, for all t ∈ [0, T],
which is the required boundedness property. The equicontinuity property can be derived easily from (14) above. For 0 ≤ t 1 ≤ t 2 ≤ T, we proved in the case α ≤ 1 that
After using the Triangle Inequality and the Mean Value Theorem, we have that
for some γ ∈ [t 1, t 2] ⊂ [0, T]. Thus, if we have
for some since S(0) is uniformly continuous in the closed interval [0, T]. Noting that the expression on the right-hand side is independent of S, t 1 and t 2, we see that the set E(U) equicontinous. In either case the Arzel‘a-Ascoli Theorem yields that E(U) is relatively compact, and hence Schauders second Fixed Point Theorem asserts that E has a fixed point. This fixed point is the required solution of the IVP (10a) and (10b). This completes the proof. □
Now we discuss the uniqueness results. Firstly we notice the following property of the operator E(defined in (13)). Thus, let S 1, S 2 ∈ C[0, T] ⊂ [0, t] and suppose there exists a constant L > 0 independent of t, S 1 and S 2 such that for all t ∈ [0, T]. Then we have
Next, we have the following result;
Theorem 2 Katugampola [7] —
Let E and U be defined as in Theorem1. Also letSuppose G1satisfies the Lipschitz condition with the Lipschitz constant L. Then
(16)
Theorem 3
(Uniqueness). LetAlso letDefine the set G as in Theorem1and let the functionbe continuous and satisfies a Lipschitz condition with respect to the second variable, i.e.
for some constant L > 0 independent of t, S 1, and S 2. Then, there exists a unique solution S ∈ C[0, T] for the IVP (10a) and (10b) .
Proof
According to Theorem 1, the IVP (10a) and (10b) has a solution. In order to prove the uniqueness, we adopt Theorem 2. In particular, we use the operator E as defined in (13) and recall that it maps the nonempty, convex and closed set to itself. We apply Weissingers Fixed Point Theorem to prove that E has a unique fixed point. Let Then, using (16) and taking the Chebyshev norms on the interval [0, T], we have
Let In order to apply the theorem, we only need to show that the series converges. It is clear from noticing that ωj is simply the power series representation of the Mittag-Leffler function hence the series converges. This completes the proof. □
5. Solution of the projected model using predictor- corrector algorithm
In order to construct the predictor-corrector method for the IVP (9), we will follow the same procedure as in Odibat and Baleanu [18] with some modifications, and then, we will study the stability of this method. For this purpose, we start from the equivalent Volterra integral equation of first equation of the system (9), which provides
| (17) |
The first step of our algorithm, under the assumption that the function G 1 to be such that a unique solution exists on some interval [0, T], consists of dividing the interval [0, T] into N unequal subintervals using the mesh points
| (18) |
where Now, we are going to generate the approximations to solve numerically the IVP (9). The basic step, assuming that we have already evaluated the approximations is that we want to get the approximation by means of the integral equation
| (19) |
Making the substitution we get
| (20) |
That is
| (21) |
Next, if we use the trapezoidal quadrature rule with respect to the weight function to approximate the integrals appear in the right-hand side of Eq. (21), replacing the function G 1(z 1/ρ, S(z 1/ρ)) by its piecewise linear interpolant with nodes chosen at the then we obtain
| (22) |
Thus, substituting the above approximations in to Eq. (21), we obtain the corrector formula for
| (23) |
where
| (24) |
The last step of our algorithm is to replace the quantity shown on the right hand side of the formula (23) with the predictor value that can be obtained by applying the one-step Adams–Bashforth method to the integral Eq. (20). In this case, by replacing the function G 1(z 1/ρ, S(z 1/ρ)) by the quantity G 1(tj, S(tj)) at each integral in Eq. (21), we get
| (25) |
Therefore, our adaptive P–C algorithm, for evaluating the approximation is completely described by the formula
| (26) |
where and the predicted value can be determined as described in Eq. (25) with the weights being defined according to (24).
Similarly we can find the solution of the rest of the equations of system (9).
So the solution of the proposed COVID-19 system (8) can be written as:
| (27) |
where
| (28) |
5.1. Stability analysis
Theorem 4
Assume that G1(t, S) in(9)satisfies the Lipschitz condition andare the solutions of predictor-corrector method(27)and(28). Then, the numerical method(27)and(28)is conditionally stable.
Proof
Let and be perturbations of respectively. Then, the following perturbation equations are obtained by using Eqs. (27) and (28)
(29) where
(30) Using the Lipschitz condition, we obtain
(31) where Also, from Eq. (3.18) in Li and Zeng [12] we derive
(32) where Substituting from Eq. (32) into Eq. (31) results
(33)
(34)
(35) where C α,2 is a positive constant only depends on α (Lemma 1) and h is assumed to be small enough. Applying Lemma 2 concludes which completes the proof. □
6. Simulation results
In this paper we consider the fractional model of COVID-19 epidemic cited from [9]. To perform numerical simulation, we use parameter value from [9], [14], which are summarized in Table 1 .
Table 1.
| Parameter | Description | Values |
|---|---|---|
| ζ | Transmission rate between susceptible individuals and | |
| asymptomatic infected individuals | ||
| δ | Transition rate between asymptomatic infected and | 0.1142 |
| reported symptomatic infected | ||
| η | Transition rate between asymptomatic infected and | 0.0285 |
| unreported symptomatic infected | ||
| ϕ | Average time symptomatic infectious have symptoms | 1/7 |
| β1 | The unreported symptomatic death rate | |
| β2 | The reported symptomatic death rate |
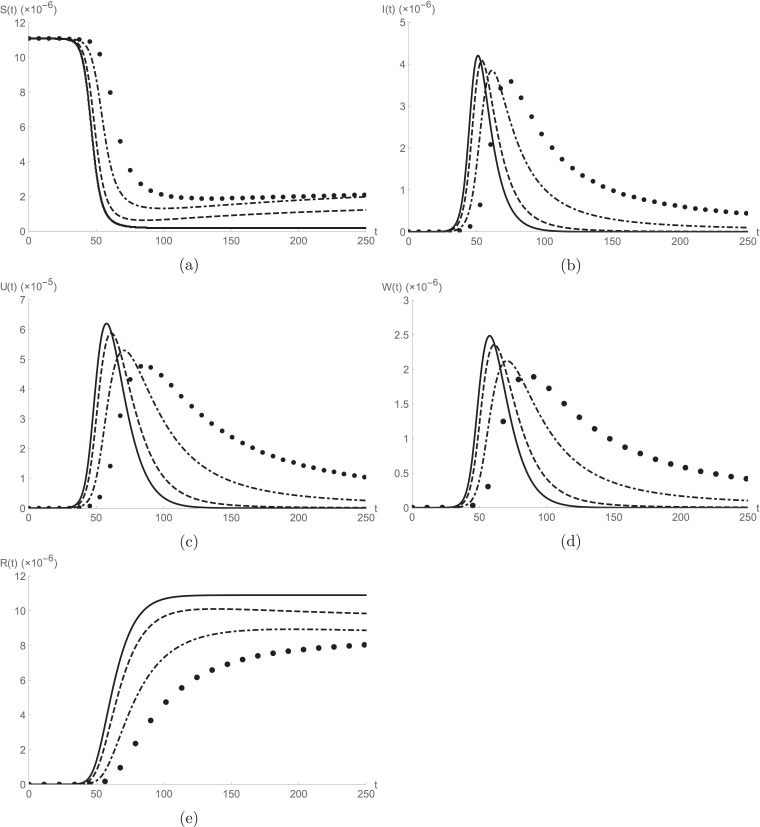
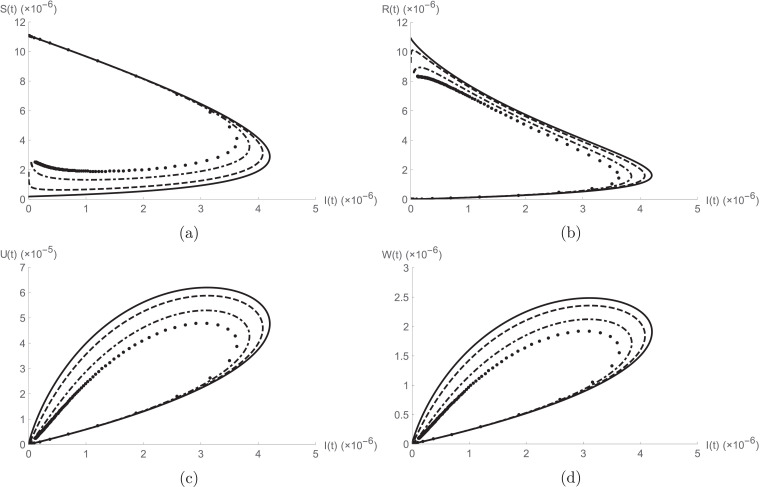
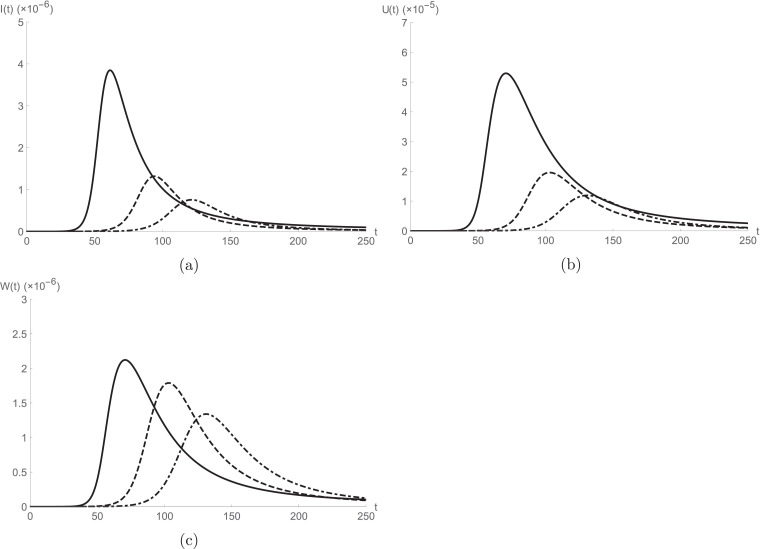
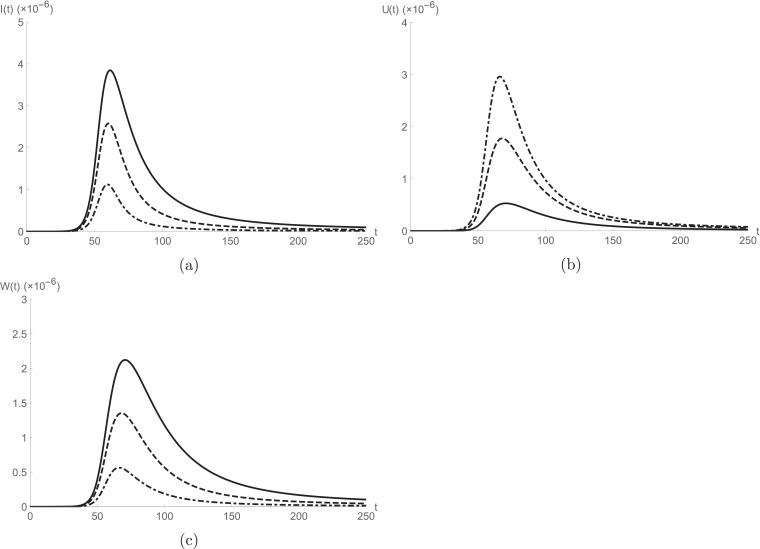
We use the following initial conditions [9], [14]. Fig. 1 exemplifies the behaviour of achieved results by projected solution procedure for S(t), I(t), U(t), W(t) and R(t) for different values of fractional order α at a fixed value of . In the collection of Fig. 2 we analyse the relationship between the asymptomatic infected people and (a) susceptible individuals, (b) reported symptomatic infected individuals, (c) unreported symptomatic infected individuals, (d) recovered individuals for different fractional order α by setting . In Figs. 3 and 4 we analyse the effects of transition rate δ and η on (a) asymptomatic infected people, (b) unreported symptomatic infected people, (c) reported symptomatic infected people used and at respectively. All graphs are computed using mathematica software. From the cited figures we can observe that the given model exceedingly depends on the order and gestures more degree of flexibility. Moreover, the fractional method gives more interesting results than the integer-order model and permit to better examine the obtained results. The graphical simulations between to are more accurate to compare with the real data. The given classes are showing acceptable nature between these values. The parameter ρ plays a very important role in the calculations. More varieties in the graphical calculations can be observed for future models at the different values of ρ.
Fig. 1.
(solid line), (dashed line), (dot-dashed line), (dotted line) for
Fig. 2.
(solid line), (dashed line), (dot-dashed line), (dotted line) for
Fig. 3.
for (solid), (dashed) and (dot-dashed).
Fig. 4.
for (solid), (dashed) and (dot-dashed).
7. Conclusions
In the last three decades, so many fatal diseases have manifest their entity in different countries all over the world. In this paper we studied the time-fractional COVID-19 model with the help of corrector-predictor method in the sense of new generalised Caputo fractional derivative. We presented the stability analysis of the proposed numerical scheme by the help of some important lemmas. The existence and uniqueness analysis of the system is also presented by the help of some important fixed point theorems. Our results are helpful to make an idea of COVID-19 cases in Wuhan, China. The nature of the achieved solution has been specified with the help of plots and which show the effect and essence generalizing the integer order system into a non- integer order system with the specific theory of fractional calculus. The projected scheme is strong and highly credible in finding the solution to fractional models of physical, biological and medical importance. In this method, we use a non-uniform grid for numerical simulations and parameter ρ gives an advantages to study the model more accurately compare to the real data. Which are the main features of this scheme. For the solution of the epidemic model, we stated various graphical results at the different values of α. The present study exemplifies the applications of the projected scheme and considered fractional operator while analysing real word problems and understanding as well as predicting the corresponding consequences.
CRediT authorship contribution statement
Vedat Suat Erturk: Conceptualization, Investigation, Software, Methodology, Writing - review & editing. Pushpendra Kumar: Conceptualization, Formal analysis, Investigation, Methodology, Resources, Visualization, Writing - original draft.
Declaration of Competing Interest
Authors declare that they have no conflict of interest.
References
- 1.Abdo M.S., Shah K., Wahash H.A., Panchal S.K. On a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative. Chaos Solitons Fractals. 2020;135:109867. doi: 10.1016/j.chaos.2020.109867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Atangana A., Baleanu D.. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. arXiv preprint arXiv:160203408; 2016.
- 3.Caputo M., Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl. 2015;1(2):1–13. [Google Scholar]
- 4.Feng Y.-Y., Yang X.-J., Liu J.-G. On overall behavior of Maxwell mechanical model by the combined Caputo fractional derivative. Chin J Phys. 2020;66:269–276. [Google Scholar]
- 5.Gao W., Veeresha P., Baskonus H.M., Prakasha D., Kumar P. A new study of unreported cases of 2019-nCoV epidemic outbreaks. Chaos Solitons Fractals. 2020;138:109929. doi: 10.1016/j.chaos.2020.109929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jajarmi A., Baleanu D. A new fractional analysis on the interaction of HIV with CD4+ T-cells. Chaos Solitons Fractals. 2018;113:221–229. [Google Scholar]
- 7.Katugampola U.N.. Existence and uniqueness results for a class of generalized fractional differential equations. arXiv preprint arXiv:14115229; 2014.
- 8.Khan M.A., Atangana A. Modeling the dynamics of novel coronavirus (2019-nCoV) with fractional derivative. Alexandria Eng J. 2020;59:2379–2389. [Google Scholar]
- 9.Khoshnaw S.H., Shahzad M., Ali M., Sultan F. A quantitative and qualitative analysis of the COVID-19 pandemic model. Chaos Solitons Fractals. 2020;138:109932. doi: 10.1016/j.chaos.2020.109932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kilbas A.. Theory and applications of fractional differential equations.
- 11.Kuniya T. Prediction of the epidemic peak of coronavirus disease in Japan, 2020. J Clin Med. 2020;9(3):789. doi: 10.3390/jcm9030789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Li C., Zeng F. The finite difference methods for fractional ordinary differential equations. Numer Funct Anal Optim. 2013;34(2):149–179. [Google Scholar]
- 13.Liang K. Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS. Infect Genet Evol. 2020;82:104306. doi: 10.1016/j.meegid.2020.104306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liu Z., Magal P., Seydi O., Webb G. Understanding unreported cases in the COVID-19epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology. 2020;9(3):50. doi: 10.3390/biology9030050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Miller K.S., Ross B. Wiley; 1993. An introduction to the fractional calculus and fractional differential equations. [Google Scholar]
- 16.Mission W.-C. J.. Report of the who-China joint mission on coronavirus disease 2019 (COVID-19). Geneva 2020.
- 17.Nadim S.S., Ghosh I., Chattopadhyay J.. Short-term predictions and prevention strategies for COVID-2019: A model based study. arXiv preprint arXiv:200308150; 2020. [DOI] [PMC free article] [PubMed]
- 18.Odibat Z., Baleanu D. Numerical simulation of initial value problems with generalized Caputo-type fractional derivatives. Appl Numer Math. 2020;156:94–105. [Google Scholar]
- 19.Oldham K., Spanier J. Elsevier; 1974. The fractional calculus theory and applications of differentiation and integration to arbitrary order. [Google Scholar]
- 20.Organization W.H., et al. Report of the who-China joint mission on coronavirus disease 2019 (COVID-19). 2020.
- 21.Podlubny I. Elsevier; 1998. Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. [Google Scholar]
- 22.Rudolf H. World Scientific; 2000. Applications of fractional calculus in physics. [Google Scholar]
- 23.Sun K., Jianbin Q., Karimi H.R., Fu Y. Event-triggered robust fuzzy adaptive finite-time control of nonlinear systems with prescribed performance. IEEE Trans Fuzzy Syst. 2020:1. [Google Scholar]
- 24.Sun K., Liu L., Qiu J., Feng G. Fuzzy adaptive finite-time fault-tolerant control for strict-feedback nonlinear systems. IEEE Trans Fuzzy Syst. 2020:1. [Google Scholar]
- 25.Sun K., Qiu J., Karimi H.R., Gao H. A novel finite-time control for nonstrict feedback saturated nonlinear systems with tracking error constraint. IEEE Trans Syst Man Cybern. 2019:1–12. [Google Scholar]
- 26.Wikipedia website Wikipedia website. Wikipedia. 2020 [Google Scholar]; https://en.wikipedia.org/wiki/coronavirus, Accessed 07/04/2020
- 27.Yang X.-J. CRC Press; 2019. General fractional derivatives: theory, methods and applications. [Google Scholar]
- 28.Zhu N., Zhang D., Wang W., Li X., Yang B., Song J., et al. A novel coronavirus from patients with pneumonia in China, 2019. New Engl J Med. 2020;382:727–733. doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]