Figure 3. Average dissociation rate constants () for the mutant and two wild-type conditions resulting from modeling interactions using a Markov model.
Error bars were estimated as the square root of the Cramèr-Rao lower bound.
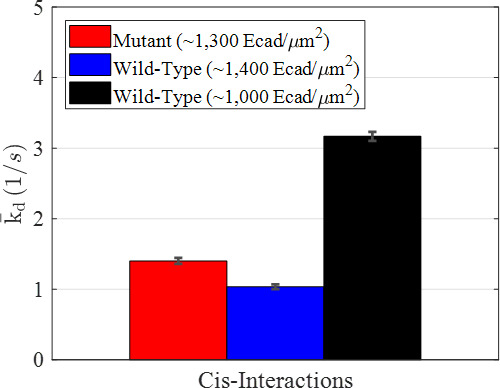
Figure 3—figure supplement 1. Complementary cumulative association time (high-FRET state dwell time) distributions calculated for each of the three high surface coverage experimental conditions and the low coverage control.
Notably, the low coverage control shows dramatically shorter dwell times than all other conditions.
Figure 3—figure supplement 2. High-FRET and low-FRET complementary cumulative surface residence time (observation time) distributions for mutant E-cad and two concentrations of wild-type E-cad.
Qualitatively comparing the two wild-type high-FRET distributions indicates the probability of a long surface residence time increases with increasing surface coverage due to stronger lateral interactions.
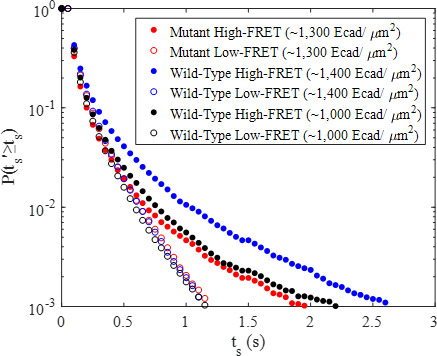
Figure 3—figure supplement 3. Complementary cumulative state dwell time distributions for the high and low-FRET states for the mutant and two wild-type E-cad conditions, compared to the predicted state dwell time distributions based upon the three-state, heterogeneous Markov model maximum likelihood estimate with beta-distributed transition probabilities.
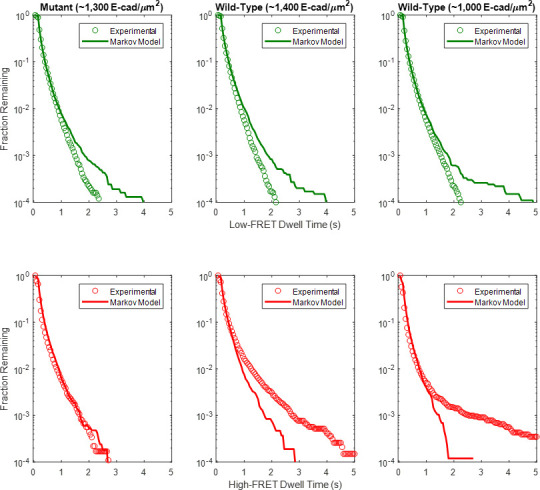
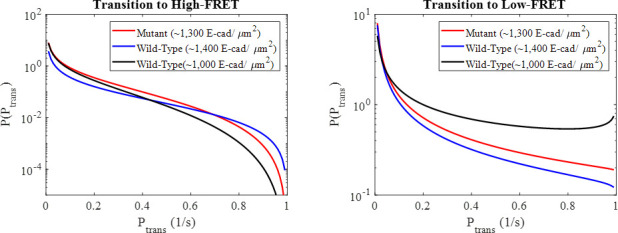
Figure 3—figure supplement 4. Probability density functions for the state transition rates between the high and low-FRET states for the mutant and wild-type conditions determined based upon the Markov model estimated, beta-distributed transition probabilities.
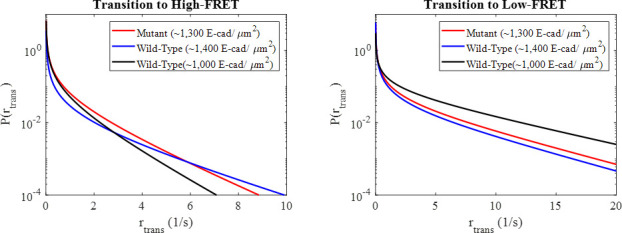
Figure 3—figure supplement 5. Low-FRET state complementary cumulative dwell time distributions for the mutant and two wild-type conditions.
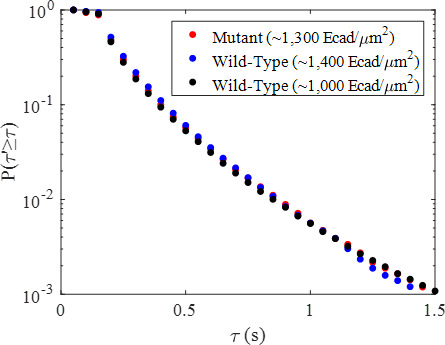
Figure 3—figure supplement 6. Beta distributions of state transition probabilities between the high and low-FRET states for the mutant and two wild-type conditions corresponding to the Markov model maximum likelihood estimated beta distribution parameters.
