Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2020 Jul 20;5(10):1262–1270. doi: 10.1038/s41564-020-0755-4

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s), under exclusive licence to Springer Nature Limited 2020

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

PMC Copyright notice

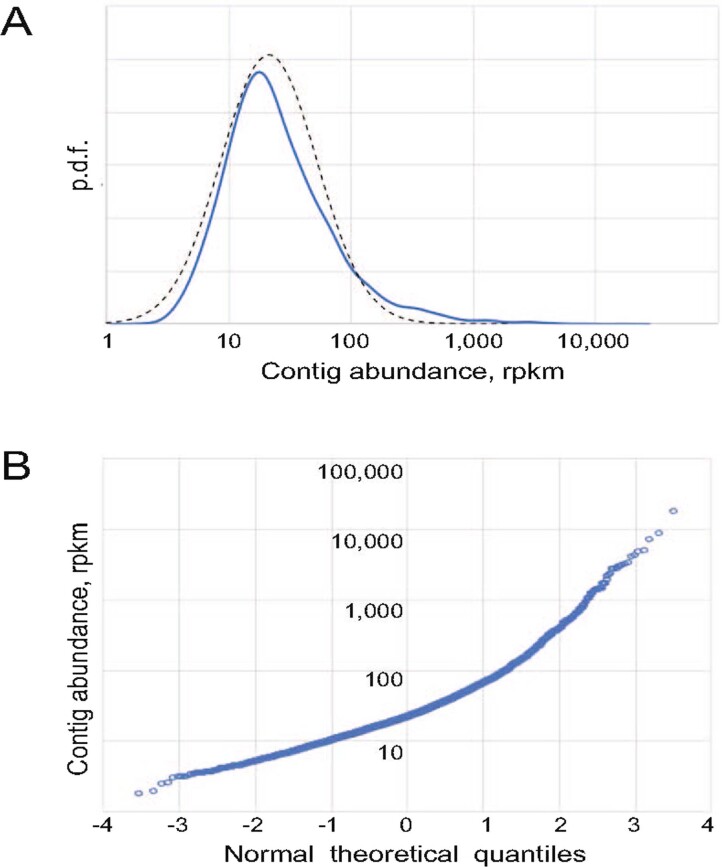
Extended Data Fig. 10 — (a) Probability density function (p.d.f.) for contig abundances (n = 4571 non-identical contigs. The dotted line plots the log-normal distribution with the same median and interquartile distance. (b) Quantile-quantile (Q-Q) plot of the distribution of contig abundances (n = 4571 non-identical contigs) versus the standard normal distribution. The figure shows that at the first approximation the distribution of contig abundances follows the log-normal distribution (typical in complex environments), but the deviations (a pronounced heavy tail of high values) hints on a dynamic environment producing superabundant viral blooms. Source data for panels (A) and (B) are presented in Source Data Figs. 1 and 2, respectively.

Source data