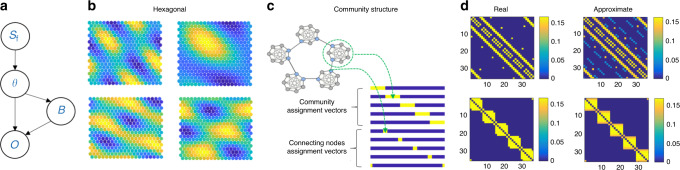
Fig. 3. Inferring graph structure rather than learning it using a basis sets representation for structural knowledge.

a We present a generative model for graphs. Each graph belongs to a structural form (S_f). Given a structural form, graph size (θ) is sampled from prior distribution (p(θ|S_f)) and the transition matrix is approximated. Given a transition matrix ($A_{sf}^{\theta }$, that is determined by the form and the dimensions) an emission matrix (B) is sampled. From these two matrices, the sequence of observations (O) can be generated. b Basis sets for Hexagonal grid, few examples. c Basis sets for a community structure. Basis sets can allow direct inference of important graph states without the need of further computation. In a graph with underlying community structure, the connecting nodes (blue circles) are important; knowing them allows fast transitions between communities. A basis set that contains explicit connecting nodes assignment vectors allows the direct inference of their identity by learning the emission matrix. d The transition matrices can be approximated using Basis sets for structural knowledge. Upper panels: correct and approximated transition structure for Hexagonal grids with 36 nodes. Lower panels: real and approximated transition matrices for a graph with underlying community structure (35 nodes).