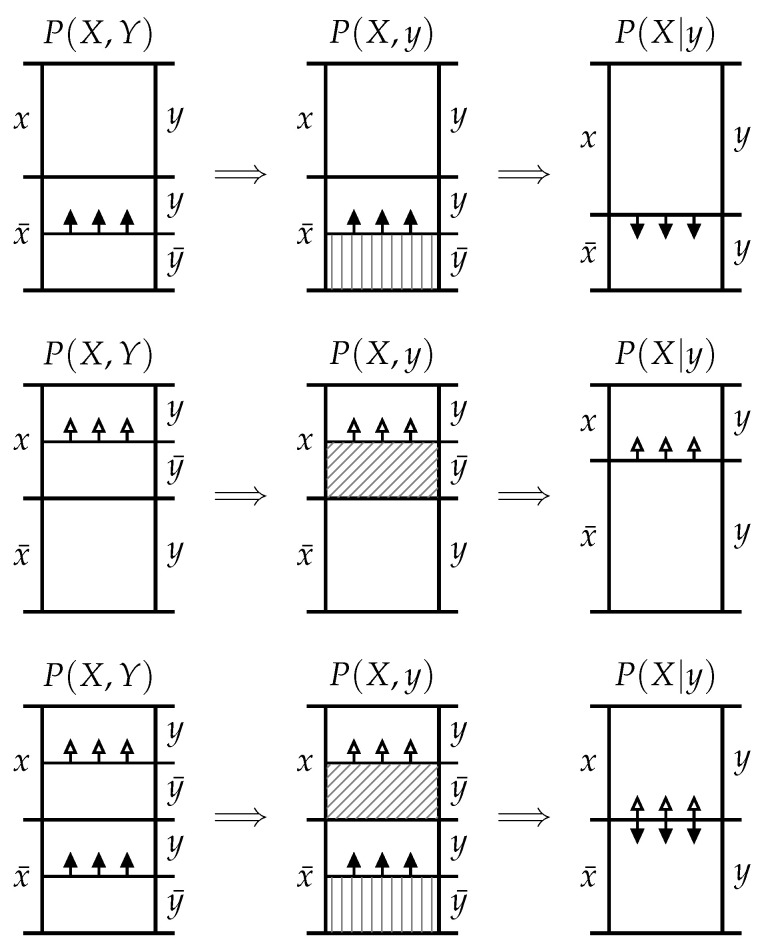
Figure 1.

In probability mass diagrams, height represents the probability mass of each joint event from $\mathcal{X}\times Y$ which must sum to 1. The leftmost of the diagrams depicts the joint distribution $P(X,Y)$, while the central diagrams depict the joint distribution after the occurence of the event $y\in \mathcal{Y}$ leads to exclusion of the probability mass associated with the complementary event $\overline{y}$. By convention, vertical and diagonal hatching represent informative and misinformative exclusions, respectively. The rightmost diagrams represent the conditional distribution after the remaining probability mass has been normalised. Top row: A purely informative probability mass exclusion, $p(\overline{x},\overline{y})>0$ and $p(x,\overline{y})=0$, leading to $p\left(x\right|y)>p(x)$ and hence $i(x;y)>0$. Middle row: A purely misinformative probability mass exclusion, $p(\overline{x},\overline{y})=0$ and $p(x,\overline{y})>0$, leading to $p\left(x\right|y)<p(x)$ and hence $i(x;y)<0$. Bottom row: The general case $p(\overline{x},\overline{y}>0)$ and $p(x,\overline{y})>0$. Whether $p\left(x\right|y)$ turns out to be greater or less than $p\left(x\right)$ depends on the size of both the informative and misinformative exclusions.