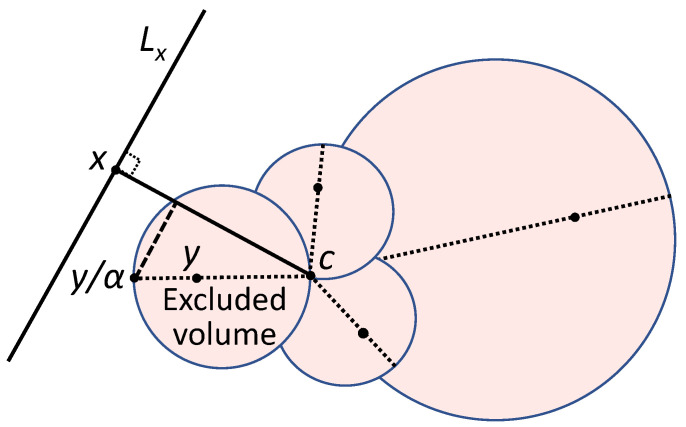
Figure 2.

Fisher’s separability of a point $\mathit{x}$ from a set Y. Diameters of the filled balls (excluded volume) are the segments $[\mathit{c},\mathit{y}/\alpha ]$ ($y\in Y$). Point $\mathit{x}$ should not belong to the excluded volume to be separable from $\mathit{y}\in Y$ by the linear discriminant (1) with threshold $\alpha$. Here, $\mathit{c}$ is the origin (centre), and $L_x=\{\mathit{z} | (\mathit{x},\mathit{z})=(\mathit{x},\mathit{x})\}$ is the hyperplane. A point $\mathit{x}$ should not belong to the union of such balls (filled) for all $\mathit{y}\in Y$ for separability from a set Y. The volume of this union, $V_{\mathrm{excl}}$, does not exceed $V_n\left({\mathbb{B}}_n\right)\left|Y\right|/{\left(2\alpha \right)}^n$.