Skip to main content
. Author manuscript; available in PMC: 2020 Sep 27.
Published in final edited form as: J Proteome Res. 2019 Jul 29;18(9):3268–3281. doi: 10.1021/acs.jproteome.9b00216

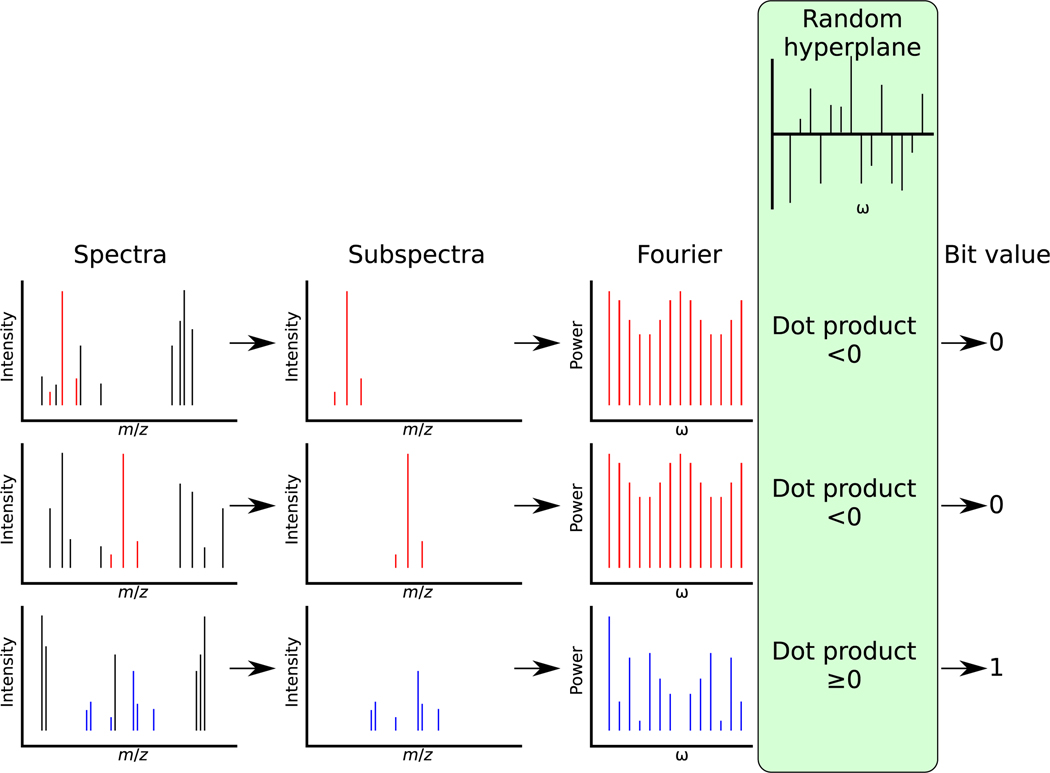
Figure 2.

Figure 2.

LSH approach to finding similar subgraphs. In the left column, three spectra are shown with the subspectra (shown in color), which are peaks contained in a connected component produced by building the graph with the estimated mass alphabet Δ. The second column shows only those peaks in the subspectrum. The third column shows the absolute values of the DFTs of the subspectra. Each of these power spectra is dot-producted with a random hyperplane, and the sign of the resulting value is used to produce a single bit. When two connected components have large subgraphs isomorphic to one another, their subspectra must be shifted versions of each other, and thus their power spectra must be nearly identical. Two subspectra drawn (first and second rows) are similar in this manner, producing similar power spectra and thus a low probability of being separated by a random hyperplane. Repeating this process with several different random hyperplanes and concatenating the bits produces a hash, which has a high probability of binning together connected components that have substantial subgraph isomorphism.