Uniform Probability Density Analysis and Population History in the Northern Rio Grande

Abstract

One of the basic challenges facing archaeology is translating surface evidence into population estimates with sufficient chronological resolution for demographic analysis. The problem is especially acute when one is working with sites inhabited across multiple chronological periods and the production curves for pottery types are uafnknown. In this paper I present a Bayesian statistical method which I call uniform probability density analysis that is tailored to this situation. This method combines uniform distributions derived from the local pottery chronology with pottery assemblage data to reconstruct the population history of individual settlements. I also illustrate applications of this method at the site and regional level using data from Cuyamungue and the surrounding Tewa Basin/VEP II New Mexico project area. The results allow one to identify a period of significant population movement corresponding to the period of Tewa ethnogenesis in the 13^th century CE.

The ability to estimate the number of people who lived in settlements and regions at various points in the past is critical for many areas of research in archaeology. This task can be relatively straightforward when one has extensive stratigraphic evidence and absolute dates from excavation or one is working with well-preserved architecture (Blakeslee 1989; Cook and Heizer 1968; Creamer 1993; Dean 1969; Graves 1983; Lekson 1986; Rohn 1971; Windes 1987). Fairly complex models can also be developed when one has strong prior knowledge of the production histories of specific artifact types (Bellanger and Husi 2012; Kohler and Blinman 1987; Ortman et al. 2007; Varien et al. 2007). Unfortunately, the task is often much more difficult: in many cases all one has to work with are the architectural footprints of sites, tabulations of associated pottery assemblages and estimates of the production spans of pottery types. In this paper I develop a Bayesian statistical method tailored to this situation and provide an example of its use in estimating the population history of a specific settlement and its surrounding area. I first briefly review previous approaches to estimating population in the study region to bring out the issues the method seeks to address. Then, I present the method, which I call uniform probability density analysis, and illustrate its use in reconstructing the population history of a specific settlement. Finally, I apply this method to a large database of archaeological settlements from the surrounding area to reconstruct the population history of this area and compare the results to those of previous studies (Ortman 2012b). Although the application in this paper has a specific geographical focus, the empirical situation it addresses is common to many areas and thus the solutions discussed should be of broad interest.

The specific settlement I consider in the case study is located within the Northern Rio Grande region of New Mexico (Figure 1). The site itself is the ancestral Tewa pueblo of Cuyamungue (LA 38, K’uuyemugeʔówînkeyi “Stones thrown down pueblo ruin”) located about 20km north of Santa Fe. Several aspects of this site make it useful for the purposes of this paper. First, the surface is relatively undisturbed and has been documented in recent fieldwork by the University of Colorado Boulder and the Pueblo of Pojoaque (Figure 2). In addition, the stratigraphic histories of at least two house mounds are known due to excavations by Fred Wendorf and Roscoe Wilmeth (Wendorf 1952; Wilmeth 1956), and records from these excavations provide a basis for translating adobe mound areas into room counts. Finally, although the site occupation began several centuries prior to the Spanish entrada, it continued to be inhabited through the Pueblo Revolt of 1680–1692 and estimates of the 17^th century population appear in Spanish documents. There is thus some basis for checking the results of uniform probability density analysis against population estimates derived from other data sources. For these reasons, Cuyamungue is a useful site for presenting the method and illustrating its application.

Figure 1.

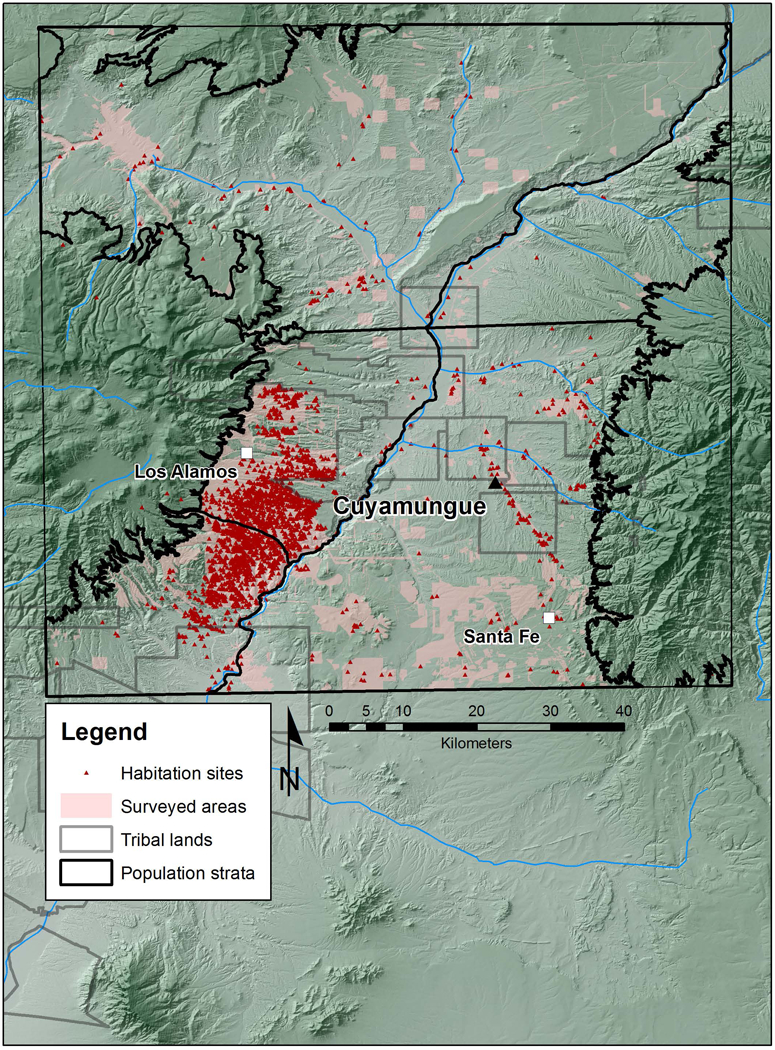
VEP II New Mexico study area and the location of Cuyamungue (LA 38).

Figure 2.

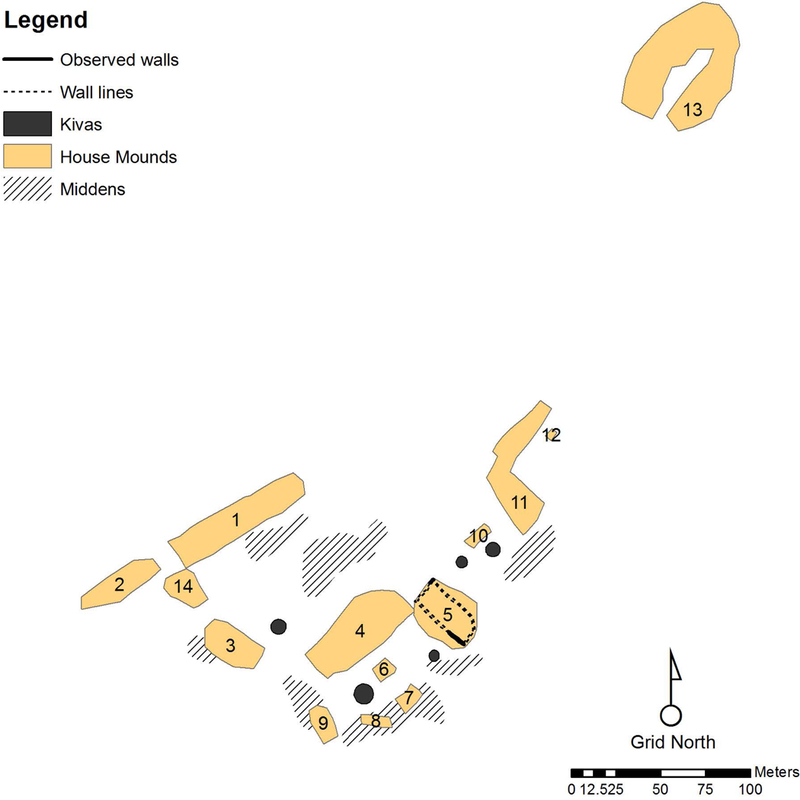
2014 Survey map of Cuyamungue (LA38). House mounds are numbered. Grid north is approximately 45 degrees west of true north.

The surrounding area I consider in the second half of the case study is one of the two study areas currently under investigation by the Village Ecodynamics Project (VEP II), a long-term project investigating human-environment interactions in the US Southwest through a combination of archaeological data synthesis, paleo-environmental reconstruction and agent-based modeling (Kohler et al. 2014; Kohler and Varien 2012). The boundary of the southern study area in north-central New Mexico corresponds to the area known as the Tewa Basin in the local archaeological literature (Anschuetz 2005, 2007; Duwe and Anschuetz 2013). The results presented here thus serve as the paleo-demographic reconstruction for the VEP II New Mexico or Tewa Basin study area. The paleo-demographic reconstruction for the northern study area, in southwest Colorado, is presented in Schwindt et al. (n.d.).

Previous methods for estimating population

Methods for estimating population typically combine measures of the living space in a settlement with data on the chronology of use of that space (Blakeslee 1989; Brown 1987; Cameron 1990; Cook and Heizer 1968; Naroll 1962; Ortman et al. 2014; Postgate 1994; Sanders et al. 1979). The simplest approach employed in the northern Rio Grande has involved apportioning the total living space uniformly across the periods of occupation suggested by the surface pottery assemblage (see Dickson 1979; Maxwell 1994; Orcutt 1999a, 1999b). To do this, one first defines pottery periods based on the beginning and end dates of the pottery types found in a region and then determines the phases of occupation for a specific site from the range of types in its pottery assemblage. Then, one allocates the total roofed living space at that site proportionately across pottery periods, taking variation in the lengths of the pottery periods and the average use-life of a structure into account.

Although this approach has the benefit of simplicity, it makes several unrealistic assumptions. First, it assumes that living space accumulates the same way as potsherds or stone flakes, such that the occupancy rate of the total architectural footprint at a site is no greater than the inverse of the periods of occupation. Excavations in Northern Rio Grande settlements (and elsewhere) demonstrate that this assumption is unrealistic. In fact, excavation results suggest that in most cases nearly the entire architectural footprint of a site was inhabited during the period of peak occupancy (see Creamer 1993; Fallon and Wening 1987; Greenlee 1933; Kohler and Root 2004; Luebben 1953; Peckham 1981; Snow 1963; Vierra et al. 2003; Wendorf 1953a). Second, this approach assumes that each square meter of an architectural mound was inhabited only for the use-life of a single room. It is almost certainly the case that the use-life of individual rooms was short. For example, Snow (1963) inferred that the average use-life of an adobe room in Northern Rio Grande sites was about 25 years based on the number of plaster layers on the walls of excavated rooms and the rate of re-plastering in historic pueblos. By comparison, the duration of the pottery periods into which living space is apportioned are often 50 years or more. Nevertheless, excavations indicate that a given square meter of mound area was often used for much longer than 25 years. For example, excavated or otherwise exposed rooms at many sites contain multiple floors, floor levels that vary across stratigraphic sections, and cultural fill consisting of melted adobe construction material and mixed refuse beneath the walls (Greenlee 1933; Stubbs and Stallings 1953:2–8; Wendorf 1953a:36–42). Snow (1963) also observed that adobe walls in Northern Rio Grande sites were often rebuilt on existing wall stubs using chunks of adobe from previous, disintegrated walls set in adobe mortar. These results indicate that standardizing the roofed living space to the average use-life of individual structures is not realistic.

An alternative approach that overcomes these issues to some extent involves apportioning the total living space across periods of occupation using a settlement history function representing the typical population trajectory of such settlements. Hill and others (2004) followed this strategy in their study of late prehistoric settlements across the U.S. Southwest (also see Wilcox et al. 2007), as did I in a previous study of Tewa Basin settlements (Ortman 2012b:Chapter 4). This approach improves upon earlier methods because it models the population history of a site in such a way that most of the architectural footprint was occupied at some point, and it recognizes that most settlements start small and grow in size over time. Indeed, many studies of villages for which construction sequences and absolute dates are available suggest that villages typically grow in a logistic fashion (for examples, see Eighmy 1979; Graves 1983; Ortman 2012b:Chapter 4). Thus, applying a settlement history function to the total architectural footprint of a site is much more realistic than dividing the total roofed living space by the number of periods of occupation. This approach also allows a given square meter of ground to have been inhabited for a much longer period than the use-life of any single structure.

Still, this approach is not ideal because it imposes a life history on a settlement when in fact this is what one would most like to reconstruct, and it is clear that the shapes of settlement histories can vary substantially. For example, within the Northern Rio Grande, Tijeras Pueblo started small and gradually grew to encompass the final architectural footprint one can see today (L. S. Cordell and Damp 2010) whereas the entire footprint of Arroyo Hondo Pueblo was established early in its occupation, after which a smaller population lingered for several decades (Creamer 1993). A more realistic way to generate a settlement history curve from surface evidence would incorporate the relative frequencies of pottery types found at the site. But this brings up the issue posed at the outset; namely, that there is often little empirical basis for estimating the frequency distributions of pottery types over time. There are a number of well-dated, short-duration contexts dating to the Coalition (A.D. 1200–1350) period (Orcutt 1999a, 1999b) but there are precious few for the Classic (A.D. 1350–1540) and Historic (A.D. 1540–1760) periods, when sites like Cuyamungue were inhabited.

In the absence of such information, researchers have often assumed that the deposition histories of pottery types follow normal or Gaussian distributions and have used this model to assess the relative intensity of occupation through time following an approach known as mean ceramic dating (Christenson 1994; Duwe 2011; Ramenofsky et al. 2009; South 1972; Steponaitis and Kintigh 1993). Recent studies have developed methods for testing whether the Gaussian assumption is reasonable in a given situation (Bellanger and Husi 2012), and in some cases it clearly is. However, the production histories of pottery types need not exhibit Gaussian distributions (see Ortman et al. 2007:Figure 3), so imposing a bell-shaped frequency distribution on the pottery types in an assemblage is in reality no better than imposing a logistic growth model on the settlement overall because both are a priori distributions that surely misrepresent at least some cases and tend to compress the occupations of sites toward the mid-points of the production spans of the earliest and latest types in the assemblage. It would therefore be most desirable to reconstruct the population history of a settlement without having to specify the shape of the frequency distributions for pottery types or the growth pattern of the architectural footprint, when they are not known beforehand. The method presented below allows one to do this while making fewer assumptions than settlement history models or mean ceramic dating. This method works from the initial assumption that each pottery type was deposited at a uniform rate per capita across its production span, and it combines this model with pottery type counts to produce an initial assessment of the relative rate of potsherd deposition through time. It then modifies the uniform assumptions of the initial analysis using Bayes’ Theorem and the relative frequencies of types in the assemblage to produce a refined assessment that allows the deposition rates of pottery types to vary across their production spans. Finally, information on the sizes of architectural mounds is used to translate this result into population estimates.

Figure 3.

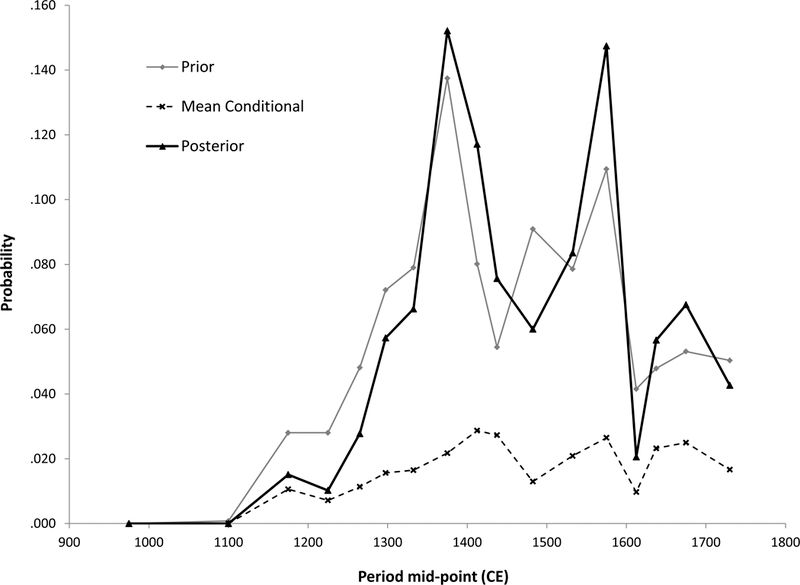
Prior, Mean Conditional, and Posterior Distributions for Area 4 (Mounds 4 and 5) at Cuyamungue.

Uniform probability density analysis

The method presented here is a form of probability density analysis as developed in my previous work (Ortman 2003:39–65; Ortman et al. 2007; Varien and Ortman 2005). However, instead of using empirical probability density distributions derived from calibration data, or theoretical distributions as in mean ceramic dating (Christenson 1994; Peeples and Schachner 2012; Ramenofsky et al. 2009), this method begins by apportioning the probability of deposition of a potsherd of a given type uniformly over the entire production span of that type, based on absolute dates and stratigraphic evidence from a given region. In statistical jargon, such distributions are referred to as uniform distributions. Table 1 presents uniform distributions for pottery types commonly found in Tewa Basin sites. The rows of the table list the pottery types, along with current assessments of their beginning and end dates of production (Dyer 2008; G. P. Wilson 2006). The columns present a series of 17 pottery periods defined on the basis of the beginning and end dates of these types, such that each period is characterized by a distinct assemblage (in other words, no two pottery periods are associated with the same list of types present). Finally, the cell values represent the number of years in each pottery period divided by the total range of each type. These values are between zero and one, and the values in each row sum to one. The values in each row thus represent the proportion of the total range of each type corresponding to each pottery period, or the probability that a potsherd of that type was deposited at a site during each of these periods.

Table 1.

Uniform distributions and pottery periods in the Tewa Basin.

Phase:	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Type	900–1050	1050–1150	1150–1200	1200–1250	1250–1280	1280–1315	1315–1350	1350–1400	1400–1425	1425–1450	1450–1515	1515–1550	1550–1600	1600–1625	1625–1650	1650–1700	1700–1760
Red Mesa B/W	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Kwahe’e B/W	0	.667	.333	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Santa Fe B/W	0	0	.250	.250	.150	.175	.175	0	0	0	0	0	0	0	0	0	0
Wiyo B/W	0	0	0	0	0	.292	.292	.417	0	0	0	0	0	0	0	0	0
SF/Wiyo B/W	0	0	.250	.250	.150	.175	.175	0	0	0	0	0	0	0	0	0	0
Biscuit A	0	0	0	0	0	0	0	.500	.250	.250	0	0	0	0	0	0	0
Biscuit B	0	0	0	0	0	0	0	0	.125	.125	.325	.175	.250	0	0	0	0
Potsuwii Incised	0	0	0	0	0	0	0	0	0	0	.650	.350	0	0	0	0	0
Biscuit, NFS	0	0	0	0	0	0	0	.200	.100	.100	.260	.140	.200	0	0	0	0
Sankawi B/C	0	0	0	0	0	0	0	0	0	0	0	.259	.370	.185	.185	0	0
White, NFS	.333	.222	.111	.111	.067	.078	.078	0	0	0	0	0	0	0	0	0	0
Kapo Black	0	0	0	0	0	0	0	0	0	0	0	0	0	0	.185	.370	.444
Tewa Polychrome	0	0	0	0	0	0	0	0	0	0	0	0	0	0	.185	.370	.444
Tewa Red	0	0	0	0	0	0	0	0	0	0	0	0	0	0	.185	.370	.444
Plain Gray1	.211	.141	.070	.070	0	0	0	0	.035	.035	.092	.049	.070	.035	.035	.070	0
Indented Corrugated	0	.435	.217	.217	.130	0	0	0	0	0	0	0	0	0	0	0	0
Smeared Indented	0	0	0	0	.171	.200	.200	.286	.143	0	0	0	0	0	0	0	0
Micaceous (plain/ribbed)	0	0	0	0	0	0	0	0	.111	.111	.289	.156	.222	.111	0	0	0
Striated (faint or heavy)	0	0	0	0	0	0	0	0	0	0	0	0	0	.250	.250	.500	0
Utility, NFS1	.174	.116	.058	.058	.035	.041	.041	.058	.029	.029	.076	.041	.058	.029	.029	.058	.070
Galisteo B/W2	0	0	0	0	0	.292	.292	.417	0	0	0	0	0	0	0	0	0
Glaze on Red/Yellow2	0	0	0	0	0	0	.259	.370	.185	.185	0	0	0	0	0	0	0
Glaze Polychrome2	0	0	0	0	0	0	.091	.130	.065	.065	.169	.091	.130	.065	.065	.130	0
Glaze A2	0	0	0	0	0	0	.318	.455	.227	0	0	0	0	0	0	0	0
Glaze B2	0	0	0	0	0	0	0	0	.500	.500	0	0	0	0	0	0	0
Glaze CD2	0	0	0	0	0	0	0	0	0	.278	.722	0	0	0	0	0	0
Glaze EF2	0	0	0	0	0	0	0	0	0	0	0	.189	.270	.135	.135	.270	0
Glaze, NFS2	0	0	0	0	0	0	.091	.130	.065	.065	.169	.091	.130	.065	.065	.130	0
Column total (local types)	1.72	1.58	1.29	.96	.70	0.96	0.96	1.46	0.79	0.65	1.69	1.17	1.172	0.61	1.06	1.74	1.40

Notes:

^1.These generic categories are excluded from prior probability calculations but incorporated into conditional probability calculations as described in the text.

^2.These nonlocal types are included only in prior probability calculations.

The rows of Table 1 represent uniform distributions because the probability of deposition of a potsherd of a given type in any given year is equal over the entire span of production of each type. The probability of deposition during a given period varies with the length of the period, but this is reasonable because, in the absence of any additional information on the shape of the production curve, a potsherd is more likely to have been deposited during a period representing a larger portion of its total production span than during a period corresponding to a shorter portion of this span. Note also that the bottom row of Table 1 also sums the probabilities assigned to each locally-produced pottery type. These sums come into play later in the analysis.

The initial step in the analysis combines these uniform distributions with a representative sample of pottery from a site to calculate a probability density distribution. This step is similar to the procedure followed by Roberts and others (2012), but in this case the purpose is to estimate the overall relative rate of sherd deposition through time. This is accomplished by (1) multiplying the uniform distribution for each pottery type by the number of potsherds of that type in the site assemblage, (2) summing the resulting distributions together, and then (3) dividing by the number of sherds in the assemblage. For example, Table 2 presents surface pottery assemblages from various areas of Cuyamungue. To calculate a “prior” distribution for Area 4, one multiplies the row corresponding to Santa Fe Black-on-white in Table 1 by 16 (the number of sherds of that type in Area 4); the row corresponding to Wiyo Black-on-white by 178, and so forth for every type in the assemblage. Then these rows are added together and divided by 3743, the total sample size. The result is a probability density distribution for which the area under the curve equals one and the height represents the probability of occupation during each of the pottery periods. These values can also be interpreted as relative rates of potsherd deposition, or the relative intensity of occupation, during each period.

Table 2.

Surface pottery assemblages at Cuyamungue.

Area:	1*	2	3	4	5	Total
Mounds:	10–12	1–3, 14	6–9	4–5	13
Santa Fe B/W	22	16	5	16	21	80
Wiyo B/W	130	179	140	178	60	687
SF/Wiyo B/W	114	141	157	338	33	783
Biscuit A	149	230	95	205	29	708
Biscuit B	22	115	129	210		476
Potsuwii Incised			5	18		23
Biscuit, NFS	24	96	127	324	2	573
Sankawi B/C	5		122	369		496
Kapo Black			4	109		113
Tewa Polychrome			19	105		124
Tewa Red			22	149		171
Plain Gray	64	283	109	506	85	1047
Indented Corrugated	9	10	27	6	14	66
Smeared Indented Corrugated	380	466	301	585	127	1859
Micaceous (plain or ribbed)	259	494	406	422	120	1701
Striated (faint or heavy)			3	66		69
Galisteo B/W			3		1	4
Glaze on R-Y	41	51	29	82	10	213
Glaze Polychrome	3	22	18	23	3	69
Glaze A	6	9	1	3	1	20
Glaze B	1	1	1	1		4
Glaze CD				7		7
Glaze EF			1	10		11
Glaze, NFS	20	10	2	11		43
Total Sherds	1249	2123	1723	3743	505	9347

^*Note: Data are counts of surface potsherds in 2m diameter “dogleash” samples located in areas of high artifact density adjacent to the mounds in each area.

A shortcoming of this initial analysis is that it does not take information on the relative frequencies of pottery types that co-occur during certain periods into account. For example, in the Cuyamungue Area 4 assemblage there are a small number of Santa Fe Black-on-white sherds and a large number of Wiyo Black-on-white sherds. Given that both types were produced between A.D. 1315 and 1350, and that Wiyo Black-on-white is much more frequent in this area, the Santa Fe sherds could have been deposited primarily during the period of overlap with Wiyo (A.D. 1280–1350), instead of being deposited uniformly over its entire production span (A.D. 1150–1350). Yet the probability density analysis discussed above apportions Santa Fe Black-on-white uniformly across its entire production span, thus imparting a greater probability of occupation to periods prior to the production of Wiyo Black-on-white than may be reasonable. It would therefore be desirable to modify the uniform distribution for each type based on the way the observed proportions of that type interact with expectations of the uniform deposition model. In terms of this specific example, it would be desirable to adjust the shape of the prior distribution to take into account the likelihood that Santa Fe Black-on-white was deposited more often during the period of overlap with Wiyo Black-on-white than in earlier periods, given the overall abundance of the later type in the assemblage.

The next step in the analysis accomplishes this using Bayes’ Theorem. This theorem can be written a number of ways, but its simplest form is:

$$P\left(H\text{|}D\right)\propto P\left(H\right)*P\left(D\text{|}H\right)$$

The theorem states that the probability (P) of a hypothesis (H), given a specific piece of data (D), is proportional to the probability of the hypothesis before the data are known times the probability of the data if the hypothesis were true. The terms on the right-hand side of the equation are known as the prior probability and conditional probability, respectively. Bayes’ Theorem provides a systematic way of combining these two parameters to produce a posterior probability of the hypothesis, which is given on the left-hand side (for additional background on Bayes’ Theorem, see Iversen (1984); and for applications in archaeology see Bayliss (2009), Bayliss and Bronk Ramsey (2004), Bronk Ramsey (2009), Buck (2004), Buck et al. (1996), Robertson (1999) and Ortman et al. (2007), among others).

Bayes’ Theorem is often adapted to situations where the hypothesis to be examined is actually a series of related hypotheses, such as the relative probability of occupation during each of a series of pottery periods. In this case, Bayes’ Theorem for the discrete case of k related hypotheses can be written as:

$$P\left(H_i\text{|}D\right)=\frac{P\left(H_i\right)*P\left(D\text{|}{H}_i\right)}{{\sum }_{i=1}^{k}P\left(H_i\right)*P\left(D\text{|}{H}_i\right)}$$ (1)

Equation 1 states that one can determine the relative probability of each of a series of related hypotheses by combining prior knowledge of the relative probability of each hypothesis with the probability of obtaining the observed sample data if each of the available alternatives were true. In this case, Bayes’ Theorem is invoked to evaluate the probability that a site was inhabited during each of a series of pottery periods, given the prior probability of occupation for each period (from the probability density analysis) and the conditional probability of obtaining the sample data from that site based on the uniform deposition model. The resulting posterior distribution presents a view of the occupational history of the site that takes both the probability density analysis and the relative frequencies of types in the assemblage into account.

For these calculations, the prior probability of occupation during each of a series of pottery periods is the value of the prior probability density distribution for that period. The conditional probability of occupation, given the model of uniform deposition, is estimated using the normal distribution in a series of steps. In Step 1, the proportion of the total probability for period i provided by type j (p_i,j) is given by equation 2:

$$p_{i,j}=\frac{t_j{u}_{i,j}}{{\sum }_{j=1}^n{t}_j{u}_{i,j}}$$ (2)

where $t_j$ is the number of sherds of type j in the assemblage and $u_{i,j}$ is the value of the uniform distribution for period i and type j. In Step 2, a normal distribution is defined for each pottery type and period based on the pottery typology. The means of these distributions (μ_i,j) are the proportion of the total probability for period j accounted for by pottery type i in the uniform distributions specified by the typology (Table 1); and standard deviations are estimated using the standard errors of these proportions, with sample size $n_j$ given by the total number of types n present in period j (including generic and nonlocal types) in accordance with equation 3:

$${\sigma }_{i,j}=\sqrt{\left(\frac{{\mu }_{i,j}*\left(1-{\mu }_{i,j}\right)}{n_j}\right)}$$ (3)

Note that, in this step, I did not calculate ${\mu }_{i,j}$ and ${\sigma }_{i,j}$ for nonlocal or generic pottery types, but I did include generic types in estimating proportions of local types, as reflected in the column totals in Table 1. I followed this procedure for two reasons: First, the relative frequencies of nonlocal types (Galisteo B/W and Glaze ware types) in an assemblage are due to trade relationships as well as people and time, so one would expect these types to accumulate at inconsistent rates relative to local types. Second, generic types (“Plain gray” and “Utility, not further specified”) occur in all periods and thus constitute a sort of background noise as opposed to a chronological signal. As a result it appears best to assume that such sherds constitute a portion of the total accumulation during any period but the actual proportions of the generic types themselves are not meaningful.

In Step 3, these normal distributions, represented by ${\mu }_{i,j}$ and ${\sigma }_{i,j}$ are used to estimate the probability of obtaining p_i,j which is to say, a sample in which the observed proportion of the total probability for period i is provided by type j, given the hypothesis of uniform deposition of that type across its production span. This is accomplished using the probability density function for the normal distribution:

$$C_{i,j}=\frac{1}{{\sigma }_{i,j}\sqrt{2\pi }}*exp\left\{-\frac{{\left(p_{i,j}-{\mu }_{i,j}\right)}^2}{2{\sigma }_{i,j}2}\right\}$$ (4)

Note once again that for the reasons given above $C_{i,j}$ is calculated only for local pottery types and not for generic and nonlocal types. In Step 4, these values are averaged across types for each period to generate a mean conditional probability distribution:

$${\widehat{C}}_j=\frac{{\sum }_{j=1}^n{C}_i}{n_j}$$ (5)

Finally, in Step 5, the prior distribution and mean conditional distribution are combined using Bayes’ Theorem (Eq. 1) to generate a posterior probability distribution that specifies the relative intensity of occupation during each pottery period. Table 3 presents the prior, mean conditional and posterior probability distributions for Area 4 at Cuyamungue. Figure 3, which presents these data in graphical form, illustrates the effect of Bayes’ Theorem on the results. Specifically, it illustrates that the resulting posterior distribution has a larger value than the prior distribution when the conditional probability is relatively high, and vise-versa when it is relatively low. In effect, this analysis has weighted the uniform distribution model in accordance with the likelihood of obtaining the observed sample from Cuyamungue Area 4, given the uniform deposition model assumed at the outset. The result is a refined view of the relative rate of potsherd deposition at Cuyamungue Area 4 through time. This posterior distribution is not a probability density function in the traditional sense because it does not represent the probability that the site was inhabited during each of the seventeen chronological periods. Rather, this distribution presents a density of probability per period. To the extent that (1) the pottery assemblage from Area 4 is representative of the total population of potsherds deposited over the course of its occupation, and (2) the per capita deposition rates of potsherds of local types were relatively consistent through time, the height of the posterior distribution should be proportional to the average number of people who used and broke pottery vessels in Area 4 over time. Thus, if these assumptions are reasonable, the posterior distribution provides an estimate of the shape of the population history of this area. This interpretation is directly analogous to the interpretation of summed radiocarbon probability density distributions as an index of relative population (Collard et al. 2010; Downey et al. 2014; Rick 1987). Given this, the remaining task is to translate the posterior distribution into absolute population levels. I discuss this final stage of the analysis below.

Table 3.

Prior, Mean Conditional and Posterior Probabilities for Area 4 at Cuyamungue.

Period	Prior	Mean Conditional	Posterior
900–1050	.00000		.00000
1050–1150	.00081	.00003	.00000
1150–1200	.02804	.01061	.01513
1200–1250	.02804	.00717	.01023
1250–1280	.04813	.01134	.02777
1280–1315	.07208	.01563	.05733
1315–1350	.07901	.01648	.06626
1350–1400	.13748	.02175	.15211
1400–1425	.08015	.02872	.11713
1425–1450	.05445	.02730	.07564
1450–1515	.09090	.01297	.06000
1515–1550	.07856	.02090	.08353
1550–1600	.10941	.02649	.14745
1600–1625	.04155	.00973	.02057
1625–1650	.04789	.02324	.05663
1650–1700	.05312	.02499	.06754
1700–1760	.05037	.01665	.04267

From probability density to population

The posterior distribution for Area 4 at Cuyamungue suggests a dynamic population history. Stratigraphic evidence from previous excavations in Area 4 suggests that it represents the actual history reasonably well. The excavations discovered three layers of superimposed rooms in this area, with Wiyo Black-on-white dominating the lowest layer, Biscuit ware dominating the middle layer, and a series of early historic, 17^th-century types dominating the upper layer (Wilmeth 1956:28–35). These excavations also uncovered evidence of about 80 ground-floor rooms in the lower and middle layers and 50 such rooms in the upper layer (Wilmeth 1956:21). This sequence, with the third component being smaller than the other two, is clearly reflected in the posterior distribution. Note also that the application of Bayes’ Theorem to the prior distribution has the result of shifting the initial occupation of this area later in time. In effect, the analysis determined that sherds whose production began in the 1200s were deposited primarily in the 1300s based on the overall composition of the assemblage. This result is also in keeping with previous excavation results. These correspondences thus support the conclusion that the posterior distribution is a reasonable representation of the shape of the population history of Area 4.

If in fact the height of the posterior distribution is proportional to the resident population, it should be possible to calibrate this curve to the architectural footprint to estimate the resident population during each period. To accomplish this, I first calculated the surface area encompassed by each mound at the site and used excavation results from Mound 5 to translate these areas into estimates of the ground floor rooms in each mound. Then I added half the ground floor room estimate to this number for those mounds that appeared to have been two stories tall, based on the height of the adobe mound in 2014. These data and calculations are given in Table 4. Finally, I used Brown’s (1987) revision of Naroll’s constant, which found that in traditional vernacular housing there is an average of one person for every 6m² of roofed space, to translate these room count estimates to maximum population estimates. This is relatively simple in this case because the average size of prehispanic rooms at Cuyamungue and other Tewa Basin sites is also 6m², so the room count is also a maximum population estimate (Ortman 2012b:Chpt. 4; Wilmeth 1956:114). The final assumption required to translate the posterior distribution into a population history is that the entire architectural footprint of an area was inhabited during the period of peak probability. This assumption is reasonable in light of excavation results from Cuyamungue and other sites in the region (see Ortman 2012b:Chpt. 4).

Table 4.

Areas and estimated rooms for house mounds at Cuyamungue.

Mound	Area	Surface Area (m2)	Number of Stories	Total estimated rooms*
1	2	1391	2	174
2	2	582	2	73
3	2	580	2	73
4	4	1489	2	186
5	4	975	2	122
6	3	97	1	8
7	3	122	1	10
8	3	95	1	8
9	3	213	1	18
10	1	86	1	7
11	1	1096	1	91
12	1	20	1	2
13	5	2733	1	228
14	2	324	1	27

^*Note: Excavations in Mound 5 determined that 80 ground floor rooms existed within this area, thus leading to a conversion of 12.18m² of mound surface area per room. In addition, for two-story mounds, $R_T=R_1+.5R_1,$ where $R_T=totalrooms$ and $R_1=1ststoryrooms.$

With these data and assumptions in hand, Table 5 combines the posterior distributions from uniform probability density analysis with the room count estimates in Table 4 to estimate the resident population of each area of Cuyamungue during each of seventeen time periods between 900 and 1760 CE. To make these estimates, I re-scaled the posterior distribution from each area so that the peak probability equals one, and then multiplied this rescaled distribution by the maximum population estimate (i.e. the room count estimate) for that area. In other words, I assumed the entire architectural footprint was inhabited during the period corresponding to the peak probability in the posterior distribution. The results suggest the northernmost, U-shaped roomblock (Area 5) was the first area to be inhabited at the beginning of the Coalition Period (1150–1350 CE), then the settlement grew rapidly and consistently between 1250 to 1400 CE, with population growing in all areas. In the 1400s and 1500s the population declined by about one half, becoming increasingly focused on Areas 2 and 4. Finally, during the 1600s a small village re-emerged in Area 4.

Table 5.

Population estimates by area, Cuyamungue.

Period	Area					Total
	1	2	3	4	5
900–1050	0	0	0	0	0	0
1050–1150	0	0	0	0	0	0
1150–1200	11	0	5	0	50	66
1200–1250	8	0	0	0	53	60
1250–1280	23	56	8	56	86	230
1280–1315	47	122	19	116	171	474
1315–1350	57	150	22	134	201	564
1350–1400	100	346	44	308	228	1026
1400–1425	53	215	29	237	81	615
1425–1450	22	130	19	153	56	381
1450–1515	28	181	26	121	54	411
1515–1550	18	114	25	169	39	365
1550–1600	16	130	34	299	36	514
1600–1625	0	0	0	42	0	42
1625–1650	0	0	0	115	0	115
1650–1700	0	0	0	137	0	137
1700–1760	0	0	0	86	0	86

One could certainly raise objections to the estimates in Table 5, as they incorporate a number of assumptions about relationships between roofed space and people, associations between middens and room blocks, and potsherd deposition rates and occupancy rates that are almost certainly inaccurate in at least some cases. Nevertheless, this analysis yields estimates for the 17^th-century population of Cuyamungue that are consistent with historic census records. For example, Spanish documents estimate the combined population of Nambe, Cuyamungue and Jacona as 600 persons in 1680. In 1641 the Nambe population is given as 300, so if the 1680 population of Nambe were similar then the combined population of Jacona and Cuyamungue at 1680 would have been around 300 persons as well. In addition, Vargas baptized thirty children at Cuyamungue in 1692 and 18 at Jacona (Wilmeth 1956:20–22). If one assumes that about twenty percent of the inhabitants were children and that Cuyamungue was of similar size to Jacona in 1680, these sources suggest Cuyamungue was home to about 150 people in the late 17^th century. This is remarkably close to the total population estimate of 137 given in Table 5, despite the fact that Spanish documents played no role in producing it, and despite the fact that the peak of the posterior distribution for Area 4 corresponds to the 1350–1400 period, not the period to which the Spanish documents refer. This correspondence thus provides at least some basis for suggesting that the methods presented here can successfully recover the population history of a settlement, given data that satisfy the assumptions behind the approach. Initial applications of these same methods at other sites where the results can be checked against Spanish documents also support this conclusion (Ortman 2012a).

From site to regional population history

In the final portion of this paper, I apply uniform probability density analysis on a larger scale to reconstruct the population history of the VEP II New Mexico study area, which largely corresponds to the Tewa Basin as defined by others (Anschuetz 2005, 2007). Such reconstructions are important due to differences of opinion among researchers regarding the processes behind the formation of ancestral Tewa society. The issues surrounding this debate are complex, but the basic issue is that Tewa oral tradition consistently refers to the central Mesa Verde region of southwestern Colorado as a place where Tewa ancestors once lived, and the population of the Tewa Basin grew substantially as the southwestern Colorado population declined, but Mesa Verde material culture does not reappear in Tewa Basin sites, or anywhere else for that matter (Boyer et al. 2010; Linda S. Cordell 1995; Curtis 1926; Kidder 1924; Kohler et al. 2010; Lakatos 2007; Lipe 2010; Mera 1935; Naranjo 1995, 2006; Ortman 2012b; Wendorf 1953b; Wendorf and Reed 1955; C. D. Wilson 2013). The absence of clear material culture continuities has led to close examination of population trends in the Tewa Basin to determine whether the timing of growth is consistent with in-migration from the northwest, and whether the rate of growth necessarily implies in-migration. Some studies have argued in-migration was required (Collins 1975; Dickson 1979), whereas others have argued that intrinsic growth could have accounted for the observed population changes (Boyer et al. 2010; Maxwell 1994).

In a previous study, I estimated the Tewa Basin population for a series of twelve chronological periods using a database of recorded site information, survey coverage, and a series of site occupation models (Ortman 2012b:Chpt. 4). I build on these efforts here, incorporating an updated site database and uniform probability density analysis where possible. A summary of the method used in the previous study is as follows:

1. I compiled a database of all recorded sites, identified those that were habitations, and determined their periods of occupation based on architectural attributes and the range of pottery types present. Surveyors typically defined a separate component for each major period of occupation at a site (Developmental, Coalition, Classic, Historic), and in such cases each component was tracked and analyzed individually.

2. I also compiled room count estimates for each component and classified each component as a house (1–12 rooms), hamlet (13–49 rooms), village (50–499 rooms) or town (500+ rooms) based on these estimates.

3. For multi-period occupations, I apportioned rooms across occupation periods according to the category of settlement: For house components I apportioned rooms evenly across occupation periods; for hamlet components, I apportioned half of the room count to each period; and for village and town components, I applied a logistic growth model derived from excavation results which modeled the occupations as starting small, then experiencing a period of growth, and then stabilizing at a peak occupancy of 90 percent of the room count during the final periods of occupation.

4. I defined five population strata based on physical geography and prior knowledge of the occupational histories of various areas. The names and locations of these strata are: Chama in the north, Pajarito in the west, Cochiti in the southwest, Santa Fe in the southeast, and Velarde in the northeast (for polygon boundaries see Figure 1). I also determined which house and hamlet components are located within surveyed areas, and determined the proportion of the area of each population stratum that had been surveyed.

5. I extrapolated the total populations of houses and hamlets based on population densities within surveyed areas within each stratum, and corrected for the relationship between use-life and period length for Coalition Period (A.D. 1200–1350) sites using occupation span estimates derived from pottery accumulations.

6. Finally, I assumed that all villages and towns are known and thus added the total estimated populations of these components to the estimates for houses and hamlets. The assumption that all sites with 50 or more rooms are known is reasonable due to sustained interest in cataloging large sites in the Northern Rio Grande over the past century (Bandelier 1892; Beal 1987; Crown et al. 1996; Fowles 2004; Harrington 1916; Hewett 1906; Hill et al. 2004; Mera 1934; Snead et al. 2004; Wilcox et al. 2007).

I utilize the same general approach here but incorporate a number of improvements completed as part of the VEP II project. First, I work with an improved database of approximately 3,000 habitation components, field houses and historic herding camps; pottery assemblage data for more than 250 components compiled from the published and gray literature, archives and recent field and laboratory work; a complete database of all known habitations within Bandelier National Monument; a review of New Mexico ARMS site files for all sites with 50 or more rooms; and improved room counts for villages and towns in the Chama stratum (Duwe 2011). Second, I refine the chronological scheme of the analysis, expanding from the twelve periods of the previous study to the seventeen periods defined in Table 1. Third, I use uniform probability density analysis, following the methods described in this paper, to estimate the population histories of all components associated with pottery tallies. Fourth, due to the fact that excavation often leads to the discovery of additional rooms that are not visible on the modern ground surface, I assume a peak occupancy rate of 100 percent, instead of 90 percent as in the previous study. Finally, I attempt to partially quantify the degree of uncertainty surrounding the resulting population estimates. Essentially, I used the same procedures as in the previous study but with an improved database, a seventeen-period chronological scheme, and uniform probability density analysis instead of apportionment or logistic growth modeling whenever possible. Table 6 summarizes the new database and the distribution of settlements by component size and location for which apportionment, logistic growth models or uniform probability density analysis was used to estimate population histories. Note in particular that, although only nine percent of components are treated using uniform probability density analysis, these sites contain about 45 percent of the total rooms in these sites. Note also that a much higher percentage of rooms from villages and towns are treated using the new method than rooms from houses and hamlets.

Table 6.

Summary of the VEP II New Mexico database

	Population reconstruction method
	Apportionment/logistic growth		Uniform probability density analysis
	Components	Rooms	Components	Rooms
A. Component type
Town	21	16435	21	22275
Village	115	12454	86	11995
Hamlet	342	7923	36	804
House(s)	1283	4696	50	352
Field house	796	1635	57	92
Herding camp	12	44
B. Component location
Velarde	9	2685	2	1300
Chama	71	3290	19	14897
Santa Fe	220	11177	35	8110
Cochiti	924	8747	144	6304
Pajarito	1345	17288	50	4907
Total	2569	43187	250	35518
% of Total	91.1	54.9	8.9	45.1

Table 7 presents the revised momentary population estimates by population stratum and settlement size class, and Figure 4 graphs these results by sampling stratum. The results illustrate that the population history of the Tewa Basin/VEP II New Mexico study area was quite dynamic. The initial population was concentrated in the Santa Fe stratum along the Tesuque and Pojoaque rivers. Then, starting around 1200 CE, a second population center developed in the Pajarito and Cochiti strata. Population growth in these areas accelerated dramatically between 1250 and 1280, after which it also picked up in the Santa Fe stratum as it leveled off in the Pajarito and Cochiti strata between 1280 and 1315 CE. In the following decades population began to decline in all three of these areas but this was compensated for by rapid growth in the Chama stratum, which suggests that most of the inhabitants of the large towns in the Chama derived from earlier settlements of the Pajarito, Chama and Santa Fe areas (Note also that >80 percent of the total habitation space in the Chama was interpreted through uniform probability density analysis, see Table 6). Recent sourcing work on Biscuit ware supports this inference of a northward drift of population during this period (Duwe 2011; Duwe and Anschuetz 2013). It is also clear that the overall population of the VEP II study area declined gradually between the middle decades of the 1400s and 1600, by which time the first Spanish capital of New Mexico had been established at Yunge-owingeh (Ellis 1989). In the early decades of the 17^th century the population of Tewa settlements declined dramatically due to a variety of factors, including captive-taking, the marriage of Pueblo women with Spaniard men, epidemic disease, and out-migration to areas beyond Spanish control (Barrett 2002; Kulisheck 2010; Ramenofsky and Feathers 2002; Trigg and Gold 2005). During the later 17^th century population increased again, most likely due to the movement of Southern Tewa populations into the study area during the Pueblo Revolt and Reconquest periods; however it declined once again after 1700 due to the departure of several groups for the Hopi Mesas (Marshall and Walt 2007) and renewed intermarriage and acculturation with Spanish populations.

Table 7.

Population estimates for the Tewa Basin/VEP II New Mexico study area

Period:	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Dates:	900–1050	1050–1150	1150–1200	1200–1250	1250–1280	1280–1315	1315–1350	1350–1400	1400–1425	1425–1450	1450–1515	1515–1550	1550–1600	1600–1625	1625–1650	1650–1700	1700–1760
Use-life:	150	100	30	30	30	30	30	30	25	25	65	35	50	25	25	50	60
Houses and hamlets in the database
Velarde	9	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Chama	43	4	12	29	52	62	88	110	78	77	61	29	31	3	23	34	27
Santa Fe	159	160	175	133	128	154	114	93	51	51	48	37	7	0	0	0	0
Cochiti	45	317	738	1088	1187	1035	889	473	246	127	174	57	33	24	24	51	16
Pajarito	60	286	557	2281	2747	2458	914	604	355	307	189	176	83	12	11	18	18
Extrapolated momentary population of houses and hamlets
Velarde	258	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Chama	517	50	88	208	629	637	903	791	942	925	730	351	370	30	280	403	327
Santa Fe	797	804	527	402	642	661	492	280	255	255	240	186	34	0	0	0	0
Cochiti	144	1021	1428	2104	3827	2862	2457	914	792	410	562	185	106	77	77	164	53
Pajarito	147	698	814	3335	6695	5134	1910	882	865	749	461	429	201	29	27	43	43
Villages and towns in the database
Velarde	0	0	24	36	399	524	598	994	875	854	1157	1289	1029	1105	1409	2783	1532
Chama	0	33	209	206	853	1951	2606	9369	12386	10493	12414	8786	9799	718	0	0	0
Santa Fe	109	1435	2000	1580	3106	5671	6342	5980	3799	1745	1338	1462	1557	1539	3045	6033	2588
Cochiti	0	69	961	1020	4549	5522	5936	4217	3237	1880	1525	1218	1059	843	870	338	660
Pajarito	102	251	1057	1686	4816	6070	5759	4529	4947	4790	3750	2735	3180	1884	1792	864	210
Total momentary population
Velarde	258	0	24	36	399	524	598	994	875	854	1157	1289	1029	1105	1409	2783	1532
Chama	517	83	297	414	1483	2588	3509	10160	13328	11417	13144	9138	10169	748	280	403	327
Santa Fe	906	2239	2527	1981	3748	6331	6834	6260	4054	2000	1578	1649	1592	1539	3045	6033	2588
Cochiti	144	1090	2389	3124	8376	8384	8393	5132	4030	2290	2088	1403	1165	920	946	502	713
Pajarito	249	949	1871	5021	11511	11204	7668	5412	5813	5538	4211	3164	3382	1913	1819	907	253
Total	2074	4360	7107	10577	25517	29031	27003	27959	28099	22100	22177	16642	17336	6225	7499	10627	5413

Note: Due to concerns over the surface visibility of sites, no use-life correction is made for Developmental Period sites. Stratum hectares (and portions surveyed) are: Velarde, 544.5 (.0349); Chama, 2057.7 (.0382); Santa Fe, 1474.5 (.1993); Cochiti, 448.0 (.3101); Pajarito, 513.3 (.4104).

Figure 4.

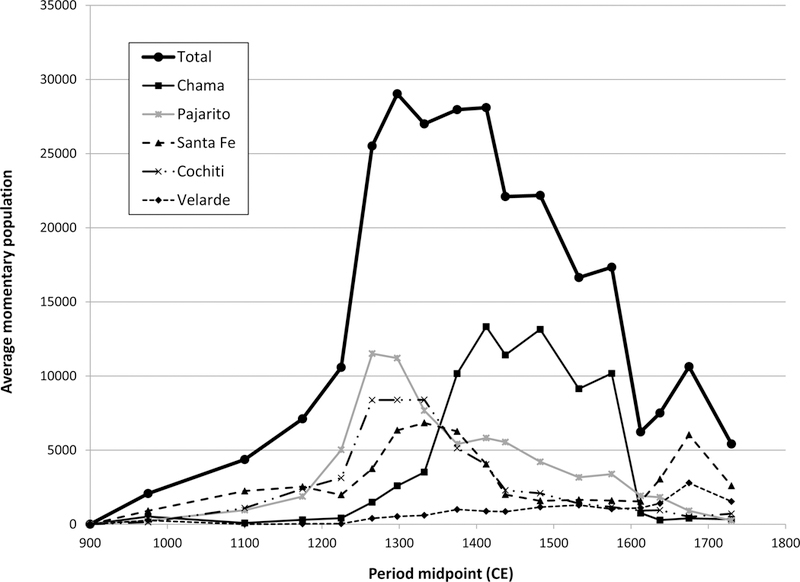
Population history of the Tewa Basin/VEP II New Mexico Study Area, by stratum.

Quantifying uncertainty

A question that is often asked but seldom answered in archaeological studies of population history is the degree of uncertainty that should be attached to the estimates generated. Due to the nature of the data and procedures utilized in this study it is not possible to calculate formal confidence intervals for the estimates in Table 7. However, it is possible to quantify at least some of the sources of uncertainty in these estimates so as to give a partial evaluation of their precision. Sources that I can control include: sampling error in pottery assemblages reflected in the conditional probability distributions calculated for each pottery type; error imposed by the apportioning procedures used for most houses and hamlets; and the sampling fraction of various population strata. There are undoubtedly additional sources of uncertainty that may be amenable to additional forms of analysis, such as bootstrapping or maximum likelihood methods. But I will leave these topics for future work and restrict the discussion here to the sources of imprecision listed above.

Table 8 summarizes the approach I took to quantifying those dimensions of uncertainty surrounding the regional population estimates mentioned above. I estimated the degree of uncertainty surrounding the total populations of villages and towns by first calculating the standard deviation of conditional probabilities for each period, across types in the assemblage, for each village or town component with a pottery tally (107 components total). I then re-scaled these to proportions by dividing the standard deviation by the maximum value of the posterior distribution for that component. Finally, I calculated the mean of these proportions for each period across components and multiplied the result by two to approximate a 95% confidence interval for the total population of villages and towns during each period. Since these error estimates are proportions, the final step is to multiply this estimate by the total population estimate for villages and towns during each period. Essentially I assume that uncertainties surrounding the population histories of villages and towns analyzed using uniform probability density analysis apply across all villages and towns. I label these results as uncertainty intervals in Table 8 so as to emphasize that they are not formal confidence intervals.

Table 8.

Uncertainty intervals for the Tewa Basin/VEP II New Mexico study area

Period:	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Dates:	900–1050	1050–1150	1150–1200	1200–1250	1250–1280	1280–1315	1315–1350	1350–1400	1400–1425	1425–1450	1450–1515	1515–1550	1550–1600	1600–1625	1625–1650	1650–1700	1700–1760
Estimates for villages and towns
Error estimate1	.0171	.0751	.1028	.0845	.0856	.0979	.1196	.0673	.0942	.0923	.1039	.1180	.0884	.0884	.1047	.0889	.0343
Uncertainty Interval2	4	134	437	383	1175	1932	2541	1688	2379	1824	2096	1827	1469	538	745	891	171
Estimates for houses and hamlets
|U-F|3	.1156	.0575	.0007	.0007	.0239	.0181	.0181	.0007	.0298	.0298	.0168	.0181	.0007	.0298	.0298	.0007	.0109
Error estimate by stratum4
Velarde	1.237	.6151	.0073	.0073	.2563	.1941	.1941	.0073	.3185	.3185	.1794	.1941	.0073	.3185	.3185	.0073	.1172
Chama	.8015	.3984	.0047	.0047	.1660	.1257	.1257	.0047	.2063	.2063	.1162	.1257	.0047	.2063	.2063	.0047	.0759
Santa Fe	.5179	.2574	.0031	.0031	.1072	.0812	.0812	.0031	.1333	.1333	.0751	.0812	.0031	.1333	.1333	.0031	.0490
Cochiti	.4152	.2064	.0025	.0025	.0860	.0651	.0651	.0025	.1069	.1069	.0602	.0651	.0025	.1069	.1069	.0025	.0393
Pajarito	.3609	.1794	.0021	.0021	.0747	.0566	.0566	.0021	.0929	.0929	.0523	.0566	.0021	.0929	.0929	.0021	.0342
Uncertainty interval by stratum5
Velarde	319	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Chama	414	20	0	1	104	80	113	4	194	191	85	44	2	6	58	2	25
Santa Fe	413	207	2	1	69	54	40	1	34	34	18	15	0	0	0	0	0
Cochiti	60	211	4	5	329	186	160	2	85	44	34	12	0	8	8	0	2
Pajarito	53	125	2	7	500	291	108	2	80	70	24	24	0	3	2	0	1

Notes:

^1.Twice the standard deviation of conditional probabilities across types within components, averaged across all components. Values are proportions.

^2.Error estimate x total population of villages and towns in the study area. Values are persons.

^3.Absolute value of the deviation between the flat distribution used in apportioning rooms and a uniform distribution. Since both distributions sum to unity across periods, these values are proportions.

^4.Square root of the squared deviation divided by the survey proportion, x2.

^5.Error estimate x total momentary population of houses and hamlets in the stratum. Values are persons.

For houses and hamlets, I followed a different approach due to the different way in which rooms were apportioned across periods of occupation and the way data from recorded sites in surveyed areas were extrapolated to un-surveyed areas. I first calculated the absolute value of the difference between 1/17^th of the 860 years encompassed by this study and the value of the uniform distribution for each period, which is equal to the number of years in the period divided by 860. I used this as an estimate of the standard error of the population apportionment process because, for most small sites, rooms were apportioned evenly across each period of occupation, whereas one could also imagine rooms being apportioned with equal probability per year across the entire span, which is equivalent to a uniform distribution. This difference was accounted for to some extent by taking the average use-life of Coalition period houses into account in producing the estimates in Table 7, but this approach at least gives one a place to begin. Next, I squared these deviations, divided by the survey proportion of each stratum, took the square root of the result, and multiplied by two to calculate an uncertainty interval for the small site population estimates for each stratum and period. These results are also a series of proportions, so in the final step I multiplied the total momentary population of each stratum for each period by the corresponding error estimate to estimate uncertainty intervals for the momentary populations of houses and hamlets within each sampling stratum during each period.

The uncertainty intervals for the total momentary population estimates of the entire study area are thus the sum of the interval for villages and towns and the interval for houses and hamlets for each stratum. The results are shown in Figure 5. In order to emphasize that these estimates are average momentary population estimates for archaeological periods, the results are displayed as bars with widths corresponding to the beginning and ending dates of each pottery period. The results illustrate that the sources of uncertainty considered here do not lead to sufficiently-broad intervals to cast doubt upon the general shape of the regional population history; especially the low population levels prior to 1150 CE and the extremely rapid buildup of population between 1200 and 1315 CE. Although there are undoubtedly other sources of error that might make these uncertainty intervals broader than they appear here, the fact that the parameters I have considered result in relatively modest intervals suggests that, at least at the level of the entire study area, the total momentary population estimates produced here are reasonably precise. The rate of population growth suggested by these data peaked at approximately three percent per year between 1250 and 1280 CE. This is far too rapid for the natural increase of an in situ population. The implication is thus that the Tewa Basin experienced a period of significant in-migration during the 13^th century CE. This migration appears to have played a central role in the formation of the Tewa society that persists to this day.

Figure 5.

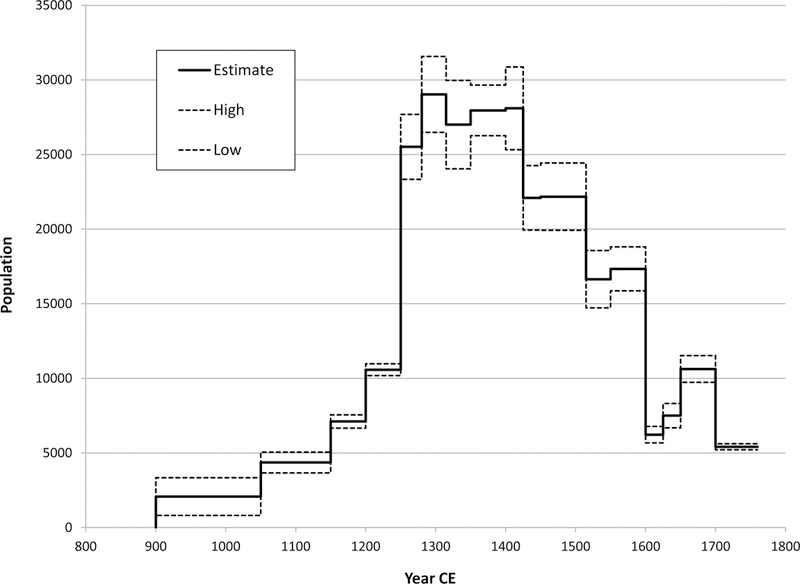
Tewa Basin/VEP II New Mexico total study area population estimates and uncertainty ranges.

This conclusion is reinforced by Figure 6, which plots the momentary population estimates for the Tewa Basin produced by this study and the new momentary population estimates produced by the VEP II for the northern (Central Mesa Verde region) study area in Southwest Colorado (Schwindt et al. n.d.). The results are once again displayed as average momentary populations for archaeological periods, bars with widths corresponding to the beginning and ending dates of each period. These results illustrate an even more striking correspondence in the timing, rate of decline, and overall magnitude of the Tewa Basin increase and the central Mesa Verde region decline in the 13^th century CE than was found in my previous study. Several points warrant special mention. First, the central Mesa Verde estimates are for a much larger area than the previous study and include all of Mesa Verde National Park and the Mancos drainage in addition to the Montezuma Valley, Dolores and Hovenweep areas. Second, in the previous study of Tewa Basin population the Late Developmental and Coalition Periods were divided into only three periods, 1050–1200, 1200–1275 and 1275–1350 CE, whereas in this study it the same interval is divided into six periods: 1050–1150, 1150–1200, 1200–1250, 1250–1280, and 1280–1315, and 1315–1350 CE. The greater subdivision of time in this study created an opportunity for more sites to be spread more evenly across periods, thus reducing the apparent population growth rate noted between the Early Coalition (1200–1275) and Late Coalition (1275–1350) periods in the previous study. Yet the result of this refined chronological scheme has been to concentrate the period of rapid population growth to an even shorter period of time, 1250–1280 CE, as opposed to 1200–1350 CE, thus leading to even higher growth rates, and even stronger evidence for in-migration during the period of the Mesa Verde collapse.

Figure 6.

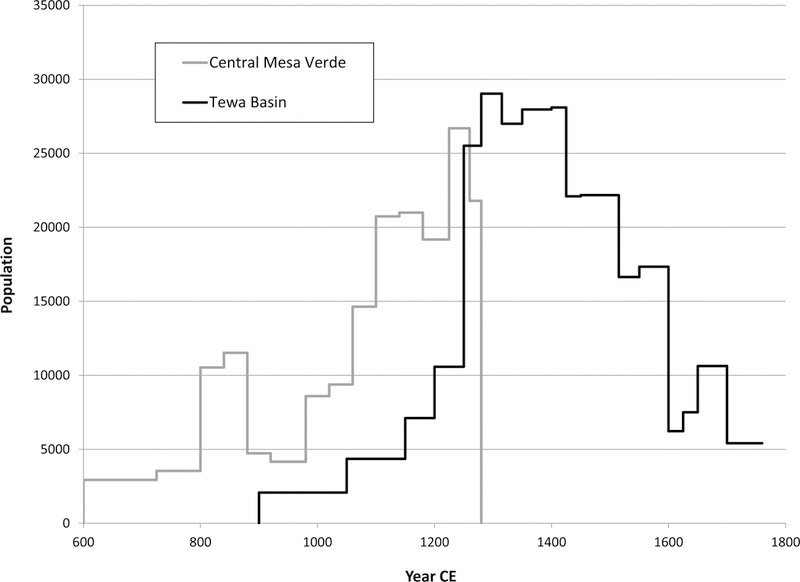
Comparison of VEP II Colorado and New Mexico population histories.

In sum, this analysis uses a refined chronological scheme and allows the growth patterns of settlements to vary more substantially than was the case in previous studies. These changes create more opportunities for discordance in the timing and magnitude of population changes between the Tewa Basin and Central Mesa Verde study areas. Nevertheless, the results show an even stronger correlation in the timing and magnitude of population decline in the north and growth in the south than was identified in the previous study. These results thus provide even stronger support for the conclusion that significant in-migration from the Central Mesa Verde region was the critical driving force in the formation of ancestral Tewa society. These demographic patterns are also consistent with oral tradition, physical anthropology, place-names, place-making practices and etymological residues in supporting this conclusion (Ortman 2008, 2010, 2011a, 2011b, 2012b).

Conclusions

In this paper I have reviewed existing methods for estimating the population histories of archaeological sites; developed a new method which I call uniform probability density analysis for assessing these histories; and applied this method to reconstruct the population history of a specific settlement and a larger region. The method makes relatively few assumptions about surface pottery assemblages and it allows these assumptions to be modulated through the use of Bayes’ Theorem. In the application presented here, the method yielded a population history for Cuyamungue that is consistent with independent stratigraphic and documentary evidence and a population history for the Tewa Basin that reinforces the role of in-migration during the 13^th century CE. These results suggest uniform probability density analysis is a useful method for reconstructing the population histories of settlements and regions when all one has to work with are the production spans of local pottery types, representative pottery assemblages, and estimates of the living space represented by total architectural footprints.

Future research could focus in a number of areas, including additional methods for characterizing uncertainty, iterative approaches that generate maximum likelihood estimates, and research that enhances control of the various parameters incorporated into the method (Ortman In Press). For example, one way to improve the chronological resolution of probability density analysis is to define additional pottery types and determine their production spans. Such knowledge allows one to define additional chronologically-distinct assemblages, and thus additional pottery periods for use in demographic reconstruction. There is a tendency toward inertia in pottery classification due to the appropriate interest in quantifying the archaeological record consistently across sites and across projects. Consistent recording is essential, for example, for multivariate seriation methods due to the role of distance matrices in the calculations. However, the approach developed here is sufficiently flexible that it can accommodate assemblages recorded at varying levels of detail so long as the pottery classification is hierarchical. Several of the types in Table 1, for example, are so-called “grouped” types (Biscuit ware, not further specified; White ware, not further specified; etc.) that were defined to accommodate sherds not clearly assignable to one of the more specific types. There is no reason in principle why the most precise types defined in Table 1 could not be further subdivided and the analysis then performed across sites recorded using either scheme. This would lead to variation in the precision of chronological interpretations but it would not invalidate the analysis or make it impossible mathematically. The ability of probability density analysis to accommodate assemblages recorded with varying levels of detail is a great advantage of this approach over multivariate seriation methods.

Another area where additional research could focus is on the definition of probability density distributions for pottery types. The method developed here is tailored to the situation where the production spans of pottery types are known but the shapes of production histories are not. I have argued that a two-step process involving uniform distributions and Bayes’ Theorem is useful in such situations, but it is important to emphasize that probability density analysis can utilize any type of probability density function, whether these be assumed on theoretical grounds (as in Christenson 1994; Peeples and Schachner 2012; Roberts et al. 2012), defined empirically (as in Kohler and Blinman 1987; Orcutt 1999a, 1999b; Ortman et al. 2007), or defined through empirical estimation of parameters of theoretical distributions (as in Bellanger and Husi 2012). Previous studies have tended to choose one type of distribution, or compare results generated using different distribution types, but in principle there is no reason in principle why different theoretical distributions could not be used for different pottery types in a single analysis if knowledge of the production histories of different types varies. This flexibility in the choice and definition of distributions deserves further exploration.

Finally, the application presented here focuses on the problem of reconstructing the population histories of sites inhabited over a series of chronological periods, but it is important to note that the same methods can also be used to “unmix” or apportion pottery assemblages to each of these periods. The first step in probability density analysis is to multiply the chosen distribution for each pottery type by the number of sherds of that type in the assemblage. These results can be used to define a “probability density assemblage” for each chronological period that provides an estimate of the relative frequency of different pottery types deposited at the site during each period. Roberts and others (2012) utilized this approach in apportioning pottery wares across occupational periods as a step in studying the evolution of regional social networks (Mills et al. 2013), and Kohler and Blinman (1987) developed methods that achieve a similar result using calibration data and multiple linear regression. That probability density analysis allows one to apportion pottery assemblages and reconstruct occupational histories simultaneously makes it an especially useful approach to the analysis of pottery assemblages from sites with widely-varying occupation spans.

As population is a critical variable for many areas of archaeological research, it is essential that archaeologists put continuous effort into methods for estimating the population histories of settlements and regions. Uniform probability density analysis is offered as a step in this on-going process.