Table 1.

Similarities between the epidemiological and reactor kinetics model.

	SIR epidemiological model	Reactor kinetic model
System	Geographical Location	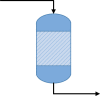Chemical Reactor
Propagation/Reaction model	$S\underset{}{\to }I\underset{}{\to }R$	Series Reaction: $A\underset{}{\to }B\underset{}{\to }C$ Auto Catalytic Reaction: $A+B\frac{k1}{\to }2B$
Model equations	$\frac{dS}{dt}=-\frac{aS\left(t\right)I\left(t\right)}{N}$ $\frac{dI}{dt}=\frac{aS\left(t\right)I\left(t\right)}{N}-bI\left(t\right)$ $\frac{dR}{dt}=bI\left(t\right)$	Series Reaction $\frac{d{C}_A}{dt}=-k_1{C}_A\left(t\right)$ $\frac{d{C}_B}{dt}=k_1{C}_A\left(t\right)-k_2{C}_B\left(t\right)$ $\frac{d{C}_C}{dt}=k_2{C}_B\left(t\right)$ Autocatalytic Reaction (in its simplest form) $\frac{d{C}_B}{dt}=k_1{C}_A\left(t\right)C_B\left(t\right)$
Responses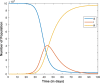
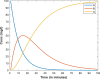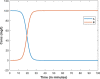
Principles of conservation	Follows conservation principles; i.e., within a geographical area, the total number of people in all of the compartments remains constant. $N=S+I+R$	Follows the conservation of mass principles; i.e., the total mass of all of the species remains constant. $M=M_A+M_B+M_C$
Rate of spread/transformations	The contagion rate is the determining factor for the states of the epidemic. It depends on the basic reproduction numbers of the epidemic, government regulations (e.g., limiting gathering size, closure of nonessential business and schools, emergency lockdown), and personal hygiene measures such as wearing masks in public places, frequent washing of hands, and social distancing.	The reaction rate governs transformations in chemical reactions. Rates of chemical transformation are often affected by the rates of other processes such as heat or mass transfer, presence of a catalyst, and species concentration, dispersion, segregation, and mixing.