Low-Temperature Rotational Tunneling of Tetrahydroborate Anions in Lithium Benzimidazolate-Borohydride Li₂(bIm)BH₄

Abstract

To investigate the dynamical properties of the novel hybrid compound, lithium benzimidazolate-borohydride Li₂(bIm)BH₄ (where bIm denotes a benzimidazolate anion, C₇N₂H₅⁻), we have used a set of complementary techniques: neutron powder diffraction, ab initio density functional theory calculations, neutron vibrational spectroscopy, nuclear magnetic resonance, neutron spin echo, and quasi-elastic neutron scattering. Our measurements performed over the temperature range from 1.5 to 385 K have revealed the exceptionally fast low-temperature reorientational motion of BH₄⁻ anions. This motion is facilitated by the unusual coordination of tetrahedral BH₄⁻ anions in Li₂(bIm)BH₄: each anion has one of its H atoms anchored within a nearly square hollow formed by four coplanar Li⁺ cations, while the remaining −BH₃ fragment extends into a relatively open space, being only loosely coordinated to other atoms. As a result, the energy barriers for reorientations of this fragment around the anchored B–H bond axis are very small, and at low temperatures, this motion can be described as rotational tunneling. The tunnel splitting derived from the neutron spin echo measurements at 3.6 K is 0.43(2) μeV. With increasing temperature, we have observed a gradual transition from the regime of low-temperature quantum dynamics to the regime of classical thermally activated jump reorientations. The jump rate of the uniaxial 3-fold reorientations reaches 5 × 10¹¹ s⁻¹ at 80 K. Nearer room temperature and above, both nuclear magnetic resonance and quasielastic neutron scattering measurements have revealed the second process of BH₄⁻ reorientations characterized by the activation energy of 261 meV. This process is several orders of magnitude slower than the uniaxial 3-fold reorientations; the corresponding jump rate reaches ~7 × 10⁸ s⁻¹ at 300 K.

Graphical Abstract

INTRODUCTION

The alkali and alkaline-earth borohydrides have attracted significant attention as promising materials for hydrogen storage.^1,2 These compounds form ionic crystals consisting of metal cations and tetrahedral BH₄⁻ anions. It is interesting to note that the tetrahedral BH₄⁻ anions can also exhibit a structure-directing effect by binding preferably via their edges. This feature may lead to unusual structures, including the porous zeolitic-like frameworks of magnesium and manganese borohydrides.^3,4 Such porous borohydrides can store hydrogen in two forms: covalently bonded H atoms in BH₄⁻ groups and physically adsorbed H₂ molecules in the pores.³ However, in contrast to zeolitic imidazolate frameworks showing a rich variety of different pore sizes and structures,⁵ borohydrides cannot be easily modified by functionalization of the building blocks. One of the possible ways to modify the structure and properties of borohydrides is to prepare hybrid compounds combining the inorganic BH₄⁻ anion and the organic imidazolate-based ligand. The first such compounds have been synthesized recently;^6,7 although they fail to exhibit any pronounced porosity, their structural features are quite remarkable. In particular, in the lithium benzimidazolate-borohydride, Li₂(bIm)BH₄ (where the benzimidazolate anion, C₇N₂H₅⁻, is denoted by bIm⁻), the BH₄⁻ anions appear to be somewhat isolated from the surrounding planar bIm⁻ anions, being only loosely coordinated on one side to four Li⁺ ions.⁷ Such an open BH₄⁻ coordination sphere is unusual among known borohydride structures.^2,8 This feature suggests low barriers for reorientational (rotational) motion of BH₄⁻ anions.

Reorientational motions of BH₄⁻ anions are known to contribute strongly to the balance of energies determining the thermodynamic stability of borohydrides. Therefore, information on the reorientational dynamics is important for understanding the fundamental properties of these compounds. The aim of the present work is to investigate hydrogen dynamics in Li₂(bIm)BH₄ using a set of complementary techniques: neutron powder diffraction (NPD), ab initio density functional theory (DFT) calculations, neutron vibrational spectroscopy (NVS), nuclear magnetic resonance (NMR), neutron spin echo (NSE), and quasi-elastic neutron scattering (QENS). Our results are consistent with the existence of the low-temperature rotational tunneling of BH₄⁻ anions in Li₂(bIm)BH₄. Although rotational tunneling has been extensively studied for −CH₃ and NH₄⁺ groups,^9,10 to the best of our knowledge, it has not been directly observed for BH₄⁻ anions in borohydrides due to the relatively large reorientational barriers typically present in these ionic compounds. Both NMR and neutron scattering results for Li₂(bIm)BH₄ are described in terms of a gradual transition from the regime of low-temperature quantum dynamics (i.e., rotational tunneling) to the regime of classical jump reorientations of BH₄⁻ anions at higher temperatures.

EXPERIMENTAL METHODS

The synthesis of the powdered Li₂(bIm)BH₄ sample was analogous to that described in ref 7. For neutron scattering measurements, the ¹¹B-enriched sample was prepared using Li¹¹BH₄ from Katchem¹¹ as a starting material; this leads to a significant reduction of the neutron absorption due to the ¹⁰B isotope in natural boron.

For NMR experiments, the sample was flame-sealed in a glass tube under 0.5 bar of nitrogen gas. NMR measurements were performed on a pulse spectrometer with quadrature phase detection at the frequencies ω_H,B/2π = 14, 28, and 90 MHz (¹H) and 28 MHz (¹¹B). The magnetic field was provided by a 2.1 T iron-core Bruker magnet. A home-built multinuclear continuous-wave NMR magnetometer working in the range of 0.32–2.15 T was used for field stabilization. For rf pulse generation, we used a home-built computer-controlled pulse programmer, the PTS frequency synthesizer (Programmed Test Sources, Inc.), and a 1 kW Kalmus wideband pulse amplifier. Typical values of the π/2 pulse length were 2–3 μs for both ¹H and ¹¹B. A probehead with the sample was placed into an Oxford Instruments CF1200 continuous-flow cryostat using helium or nitrogen as a cooling agent. The sample temperature, monitored by a chromel-(Au-Fe) thermocouple, was stable at ±0.1 K. The nuclear spin–lattice relaxation rates were measured using the saturation–recovery method. NMR spectra were recorded by Fourier transforming the solid echo signals (pulse sequence π/2_x−t−π/2_y).

Neutron scattering measurements were performed at the National Institute of Standards and Technology Center for Neutron Research. Neutron powder diffraction (NPD) measurements were performed at 6 temperatures between 2.5 and 298 K on the BT-1 High-Resolution Neutron Powder Diffractometer¹² using the Cu(311) monochromator [λ = 1.5397(2) Å; 3° ≤ 2θ ≤ 168°] with an in-pile collimation of 60 min of arc. Rietveld structural refinements were performed using the GSAS package.¹³ Neutron vibrational spectroscopy (NVS) measurements were performed at 4 K on the Filter-Analyzer Neutron Spectrometer (FANS)¹⁴ using the Cu(220) monochromator with pre- and post-collimations of 20′ of arc, yielding a full width at half-maximum energy resolution of about 3% of the neutron energy transfer. High-resolution inelastic and quasi-elastic neutron scattering (QENS) measurements were performed on three complementary instruments: the Disc Chopper Spectrometer (DCS)¹⁵ between 4 and 153 K using various incident neutron wavelengths (λ) of 1.8 Å (25.2 meV), 2.75 Å (10.8 meV), and 4.8 Å (3.55 meV) with respective elastic scattering resolutions of 2.04 meV, 275 μeV, and 118 μeV full width at half-maximum (fwhm) and respective maximum attainable Q values of around 6.56, 4.29, and 2.46 Å⁻¹; the High-Flux Backscattering Spectrometer (HFBS)¹⁶ between 1.5 and 385 K using an incident neutron wavelength of 6.27 Å (2.08 meV) with a resolution of 0.8 μeV fwhm and a maximum attainable Q value of 1.75 Å⁻¹, and the NGA neutron spin echo spectrometer (NSE)¹⁷ at 3.6, 20, and 30 K using an incident neutron wavelength of 5.0 Å (3.27 meV, Δλ/λ ≈ 0.17) for Fourier times up to 10 ns at a Q value of 1.65 Å⁻¹, where coherent scattering contributions were negligible. Instrumental resolution function free of any contaminating low-energy inelastic or quasi-elastic scattering was determined from a geometrically identical V annulus. For DCS measurements containing broad quasi-elastic scattering, the 4 K sample spectrum was also sufficient for use as a resolution function. All neutron scattering data were analyzed using the DAVE software package.¹⁸

To aid the structural model refinements of the NPD data, first-principles calculations were performed within the plane-wave implementation of the generalized gradient approximation to density functional theory (DFT) using a Vanderbilt-type ultrasoft potential with Perdew–Burke–Ernzerhof exchange.¹⁹ A cutoff energy of 544 eV and a 2 × 4 × 4 k-point mesh (generated using the Monkhorst–Pack scheme) were used and found to be enough for the total energy to converge within 0.01 meV per atom. For comparison with the NVS measurements, simulated phonon density of states (PDOSs) were generated from the DFT-optimized structure using the supercell method (2 × 2 × 2 cell size) with finite displacements^20,21 and were appropriately weighted to take into account the total neutron scattering cross-sections of H, ¹¹B, Li, C, and N.

Structural depictions were made using Visualization for Electronic and Structural Analysis (VESTA) software.²² For all figures, standard uncertainties are commensurate with the observed scatter in the data, if not explicitly designated by vertical error bars.

RESULTS AND DISCUSSION

Structural Behavior and Vibrational Dynamics of Li₂(bIm)BH₄.

Prior room-temperature synchrotron XRD measurements of Li₂(bIm)BH₄ suggested a structure with orthorhombic symmetry, but the exact orientation of the tetrahedral BH₄⁻ anions within the lattice remained unknown.⁷ Energy-minimization of this orthorhombic (space group C222₁) structure upon releasing the symmetry restrictions suggested a rather unusual BH₄⁻ anion orientation at 0 K, with one of the tetrahedral B–H bond axes extending into the adjacent near-square-planar hollow formed by four Li⁺ cations. This theoretical result was corroborated by Rietveld model refinement of the Li₂(bIm)¹¹BH₄ NPD pattern collected at 2.5 K (see Figure S1 of the Supporting Information). Aside from the refined BH₄⁻ orientation, the resulting low-temperature refined structure is largely consistent with the previously reported, room-temperature, orthorhombic structural arrangement, but modified slightly by the presence of a small monoclinic distortion of the compound (space group C2/m, β = 90.56(1)°) away from orthorhombic symmetry. Figure 1 depicts this low-temperature monoclinic structure and high-lights the unusual open coordination of each BH₄⁻ anion that allows three of its four H atoms to remain largely unrestricted to undergo facile reorientations around the more anchored B–H bond axis.

Figure 1.

(a) View of the monoclinic (space group C2/m) unit-cell structure of Li₂(bIm)BH₄ determined from the 2.5 K NPD pattern of Li₂(bIm)¹¹BH₄. Red, green, black, blue, and gray spheres denote the Li, B, C, N, and H atoms, respectively. Planar benzimidazolate (C₇N₂H₅)⁻ and tetrahedral (BH₄) anions are both clearly distinguished. (b) Schematic highlighting the unusual coordination of each tetrahedral BH₄⁻ anion in Li₂(bIm)BH₄, with one B–H bond directed into a Li₄ nearly square hollow, allowing for facile reorientations of the other three H atoms around this bond axis (as depicted by the dashed ellipse) without any significant steric interference from neighboring benzimidazolate anions.

At the increasingly higher temperatures measured (35, 50, 80, 198, and 298 K; see Figures S2–S6 of the Supporting Information), NPD data can still be well fitted using the C2/m model. However, the monoclinic distortion appears to decrease with increasing temperature. In particular, the angle β resulting from the fits changes from 90.56° at 2.5 K to 90.14° at 298 K. At room temperature, the monoclinic model (C2/m) fits the NPD data only slightly better than the orthorhombic models (C222₁ and Cmcm). Temperature dependences of the monoclinic angle β and the unit-cell volume V resulting from the NPD fits are shown in Figure S7 of the Supporting Information. It can be seen that both β and V exhibit unusual behavior in the range 35–50 K, which suggests some subtle structural changes in this region. Another interesting feature of the NPD fits is that the thermal factors for three H atoms of the BH₄ group are anomalously large at 2.5 and 35 K (see.cif files in the Supporting Information); this may be related to the unusual dynamical behavior, to be discussed below. It should also be noted that, in addition to the main monoclinic Li₂(bIm)BH₄ phase, neutron diffraction patterns indicate the presence of a residual Li(bIm) compound (space group Pmca) used in the synthesis. The content of this minor phase remains nearly constant (~11 wt %) at all temperatures.

The neutron vibrational spectrum for Li₂(bIm)¹¹BH₄ at 4 K based on FANS measurements is shown in Figure S8 of the Supporting Information compared with the simulated PDOS from the DFT-optimized monoclinic structure, indicating overall good agreement between experiment and theory. Further information about the character, symmetry, and energies of the different phonon normal mode vibrations contributing to the simulated PDOSs can be found in the Supporting Information. We note that the level of agreement is sensitive to the exact orientation of the BH₄⁻ anions within the unit-cell structure.

Figure 2 displays the temperature behavior of the two normal mode vibrational features near 10.5 and 16.1 meV (measured in neutron energy loss with DCS using 1.8 Å incident neutrons), which are dominated by BH₄⁻ anion librational (torsional) motions around the Li₄⁻anchored B–H bond axes (see the corresponding animation files in the Supporting Information). The energies of BH₄⁻ librational modes around other axes are located in the much higher range of 50–60 meV, and the BH₄⁻ bending modes in the range of 130–160 meV (see Figure S8 of the Supporting Information). The structure in Figure 1 shows that the BH₄⁻ anions are arranged in chains along the c direction (in alternating orientations of one up then one down, etc.) in association with the accompanying double-row chains of Li⁺ cations. For the 10.5 meV feature, the collection of BH₄⁻ torsional oscillations along each chain occurs in the same direction (in synchronization), whereas for the 16.1 meV feature, the directions of the oscillations for each successive BH₄⁻ along a given chain are reversed. Moreover, the lower-energy mode involves some additional noticeable minor motions from the benzimidazolate anions, whereas, the higher-energy mode is comprised almost entirely of BH₄⁻ torsional oscillations. It is evident that the appearance of this bimodal distribution of torsional energies (instead of a single normal mode energy) signals the presence of some degree of lattice-mediated coupling between BH₄⁻ rotors along the chains.

Figure 2.

Neutron vibrational spectra measured with DCS for Li₂(bIm)¹¹BH₄ in the low-energy region, indicating the temperature behavior of the two normal mode vibrational features dominated by BH₄⁻ anion librational (torsional) motions around the Li₄-anchored B–H bond axes.

Reorientational Dynamics of BH₄ Anions.

Nuclear Magnetic Resonance Results.

The reorientational dynamics associated with the unusual coordination of BH₄⁻ anions in Li₂(bIm)BH₄ were first investigated by NMR. Measurements of the proton spin–lattice relaxation rate, $R_1^{\text{H}}$, are known as a particularly effective method of probing H jump motion in borohydrides over wide dynamic ranges.²³ For most of the studied borohydrides, the dominant relaxation mechanism is due to time-dependent dipole–dipole interactions between nuclear spins. The corresponding contribution to $R_1^{\text{H}}(T)$ shows a maximum at the temperature at which the proton jump rate τ⁻¹(T) becomes nearly equal to the nuclear magnetic resonance frequency ω_H, i.e., when ω_Hτ ≈ 1. According to the standard theory,²⁴ in the limit of slow motion (ω_Hτ ≫ 1), $R_1^{\text{H}}$ is proportional to ${\omega }_{\text{H}}^{-2}{\tau }^{-1}$, and in the limit of fast motion (ω_Hτ ≪ 1), $R_1^{\text{H}}$ is proportional to τ, being frequency-independent. If the temperature dependence of the jump rate τ⁻¹ follows the Arrhenius law

$${\tau }^{-1}={\tau }_0^{-1}\text{exp}\left(-E_{\text{a}}/k_{\text{B}}T\right)$$ (1)

where E_a is the activation energy and k_B is the Boltzmann constant, the plot of ln $R_1^{\text{H}}$ vs T ⁻¹ is expected to be linear in the limits of both slow and fast motion with the respective slopes of −E_a/k_B and E_a/k_B.

The measured proton spin–lattice relaxation rate in Li₂(bIm)BH₄ exhibits two frequency-dependent peaks in the studied temperature range of 10–306 K (see Figure 3); one peak is observed near 270 K, and the other near 28 K. Such a behavior indicates a coexistence of at least two types of atomic motion with strongly differing characteristic jump rates. It should be noted that the two-peak temperature dependence of $R_1^{\text{H}}$ has been observed previously for a number of borohydride-based systems.^25–28 However, the specific feature of Li₂(bIm)BH₄ is that one of the $R_1^{\text{H}}(T)$ peaks occurs at unusually low temperature; this suggests the presence of an extremely fast H motion down to low temperatures.

Figure 3.

Temperature dependences of the proton spin–lattice relaxation rates measured at 14, 28, and 90 MHz for Li₂(bIm)BH₄.

Although boron atoms do not participate in the reorientational motion of BH₄⁻ anions, 11B spin–lattice relaxation measurements can probe the reorientations via the fluctuating ¹¹B−¹H dipole–dipole and electric quadrupole interactions. However, the recovery of the ¹¹B nuclear magnetization in borohydrides often deviates from a single-exponential behavior;^29–31 this can be attributed²⁴ to the non-zero electric quadrupole moment of ¹¹B. For Li₂(bIm)BH₄, the recovery of the ¹¹B nuclear magnetization can be reasonably approximated by a sum of two exponential functions over the entire temperature range studied. The temperature dependence of the fast (dominant) component of the 11B spin–lattice relaxation rate, $R_{1\text{f}}^{\text{B}}$, at 28 MHz is shown in Figure S9 of the Supporting Information. It can be seen that the temperature dependence of $R_{1\text{f}}^{\text{B}}$ also exhibits two peaks, and these peaks occur in the same temperature ranges as the corresponding $R_1^{\text{H}}(T)$ peaks. Thus, the ¹¹B relaxation results suggest that both $R_1^{\text{H}}(T)$ peaks in Li₂(bIm)(BH₄) are associated with different types of motion of BH₄⁻ anions, not with some H motion in the benzimidazolate anions.

Figure 4 shows the measured proton relaxation rates at ω_H/2π = 14 and 28 MHz in the region of the high-T peak as a function of inverse temperature. General features of the data in this region are consistent with the predictions of the standard theory,²⁴ as discussed above. Thus, for parametrization of the $R_1^{\text{H}}(T)$ data in this region, we have used the Arrhenius law (eq 1) and the standard relation between $R_1^{\text{H}}$ and τ (see, e.g., eq 1 of ref 32). The fit parameters are the activation energy E_a, the pre-exponential factor τ₀ in the Arrhenius law, and the amplitude parameter determined by the strength of the fluctuating part of the dipole–dipole interactions. These parameters have been varied to find the best fit to the $R_1^{\text{H}}(T)$ data at two resonance frequencies simultaneously. The results of the simultaneous fit over the T range of 198–306 K are shown by solid lines in Figure 4; the corresponding motional parameters are E_a = 261(4) meV and τ₀ = 1.4(2) × 10⁻¹³ s. It should be noted that the E_a value derived from the fit is in the range of typical activation energies for BH₄ reorientations in borohydrides.^23,33 However, the amplitude of the high-T relaxation rate peak is lower than that typically observed in borohydrides.^23,33

Figure 4.

Proton spin–lattice relaxation rates measured at 14 and 28 MHz in the region of the high-temperature peak as a function of inverse temperature. Solid lines show the simultaneous fit of the standard model to the data.

In the region of the low-temperature peak, $R_1^{\text{H}}$ measurements were performed at three resonance frequencies: 14, 28, and 90 MHz. Figure 5 shows the measured proton spin–lattice relaxation rates in this region as a function of inverse temperature. As can be seen from this figure, the behavior of $R_1^{\text{H}}$ near the peak significantly deviates from that predicted by the standard model for thermally activated atomic motion. In particular, the high-temperature slope of the $\text{log}{R}_1^{\text{H}}$ vs T⁻¹ plot appears to be steeper than the low-temperature slope, and the frequency dependence of $R_1^{\text{H}}$ near the peak is considerably weaker than that predicted by the standard model. The leveling-off of the relaxation rates toward a constant plateau below 16 K (Figure 5) can be attributed to an additional “background” contribution due to spin diffusion to paramagnetic impurities.³⁴ Furthermore, the measured ¹H NMR spectrum for Li₂(bIm)BH₄ does not exhibit any significant changes related to motional narrowing²⁴ over the broad temperature range (6–298 K). Figure S10 of the Supporting Information shows the temperature dependence of the width Δ_H (fwhm) of the ¹H NMR line measured at 28 MHz. Even at 6 K, the experimental value of Δ_H (30 kHz) is considerably smaller than that estimated on the basis of the second-moment calculations for the “rigid lattice” (53.1 kHz). This means that the dipole–dipole interactions for ¹H spins in Li₂(bIm)BH₄ are partially averaged out even at very low temperatures. Such a behavior is typical of the case of rotational tunneling.³⁵

Figure 5.

Proton spin–lattice relaxation rates measured at 14, 28, and 90 MHz in the region of the low-temperature peak as a function of inverse temperature. Solid lines show the simultaneous fit of the model based on eqs 2 and 3 to the data.

The usual approach to the description of rotational tunneling effects on the proton spin–lattice relaxation governed by fluctuating dipole–dipole interactions is based on the model introduced by Haupt.³⁶ Taking into account the background contribution to the relaxation rate, B, the corresponding expression for $R_1^{\text{H}}$ can be written as

$$R_1^{\text{H}}=C_1\sum _{n=-2}^2\frac{n^2{\tau }_{\text{c}}}{1+{\left({\omega }_{\text{t}}+n{\omega }_{\text{H}}\right)}^2{\tau }_{\text{c}}^2}+C_2\sum _{n=1}^2\frac{n^2{\tau }_{\text{c}}}{1+n^2{\omega }_{\text{H}}^2{\tau }_{\text{c}}^2}+B$$ (2)

The first term in eq 2 with the relaxation strength C₁ arises from fluctuations of the “intramolecular” dipole–dipole interactions due to transitions between the tunneling-split states of the rotor. This term contains the tunneling frequency ω_t that determines the splitting, ℏω_t, where ℏ is the reduced Planck constant. If ω_t is much larger than the resonance (Larmor) frequency ω_H, the first term becomes ω_H-independent; this leads to the characteristic frequency-independent “shoulder” at the high-temperature slope of the $R_1^{\text{H}}(T)$ peak.³⁶⁻³⁸ In the case of Li₂(bIm)BH₄, the observed frequency dependence of $R_1^{\text{H}}$ near the peak suggests that ω_t is of the order of ω_H.³⁷ The second term in eq 2 with the relaxation strength C₂ arises from fluctuations of the “intermolecular” dipole–dipole interactions; the form of this term corresponds to the classical expression for the spin–lattice relaxation rate. The correlation time τ_c for dipole–dipole interactions is determined by the lifetime of the tunneling states at low temperatures and by the mean H residence times at high temperatures; the temperature dependence of τ_c is usually approximated by the expression³⁷

$${\tau }_{\text{c}}^{-1}={\tau }_{01}^{-1}\text{exp}\left(-E_{01}/k_{\text{B}}T\right)+{\tau }_{02}^{-1}\text{exp}\left(-E_{\text{a}2}/k_{\text{B}}T\right)$$ (3)

describing a smooth transition from quantum dynamics at low temperatures to classical behavior at higher temperatures. Here, E₀₁ is the energy difference between the librational ground state and the first excited state, and E_a2 is the classical activation energy related to the potential barrier height. For parametrization of the experimental $R_1^{\text{H}}(T)$ data in the region of the low-temperature peak, we have used the model based on eqs 2 and 3. The fit parameters (C₁, C₂, B, ω_t, E₀₁, E_a2, τ₀₁, and τ₀₂) have been varied to find the best fit to the $R_1^{\text{H}}(T)$ data at the three resonance frequencies simultaneously. The results of the simultaneous fit over the temperature range of 10–54 K are shown by solid lines in Figure 5; the corresponding parameters are C₁ = 1.1(1) × 10⁹ s⁻², C₂ = 2.1(1) × 10⁹ s⁻², B = 0.60(3) s⁻¹, ω_t = 7.5(3) × 10⁸ s⁻¹, E₀₁ = 17.7(8) meV, E_a2 = 44.1(2) meV, τ₀₁ = 4.5(2) × 10⁻¹²s, and τ₀₂ = 6.2(3) × 10⁻¹⁶s. Note that the value of ω_t resulting from the fit is indeed close to the upper limit of the range of the Larmor frequencies ω_H (8.8 × 10⁷ to 5.7 × 10⁸ s⁻¹) in our experiments. In energy units, this ω_t value corresponds to a splitting of 0.49 μeV. To verify the presence of this splitting, we have employed the neutron spin echo spectrometer NSE, which provides the best energy resolution among available neutron spectrometers.

Neutron Spin Echo.

The neutron spin echo technique directly probes the neutron energy changes in the scattering process using the neutron spin precession period in a magnetic field as the internal clock. The quantity measured by NSE is proportional to the intermediate scattering function I(Q, t)—the time Fourier transform of the scattering function S(Q, ω), where ℏω is the neutron energy transfer and ℏQ is the neutron momentum transfer. In our case, the scattering function is dominated by the incoherent part. For stochastic H motion, S(Q, ω) is represented by a single line centered at zero-energy transfer, and I(Q, t) should be a monotonically decreasing function of time which can often be described by an exponential decay or a sum of exponentially decaying functions.¹⁷ In the case of the tunnel splitting, in addition to the line centered at zero-energy transfer, S(Q, ω) should contain a number of lines centered at finite energy transfers; therefore, one can expect an oscillatory behavior of I(Q, t).

Figure 6 shows the results of NSE measurements (normalized by the resolution function) for Li₂(bIm)(BH₄) at Q = 1.65 Å⁻¹ and increasing temperatures of 3.6, 20, and 30 K. It can be seen that at 3.6 and 20 K the intermediate scattering function contains an oscillatory part which is especially pronounced at 3.6 K. Such a behavior is direct evidence for the low-temperature tunnel splitting in Li₂(bIm)(BH₄). The period of the oscillations is determined by the splitting value, and the damping of the oscillations is determined by the width of the tunnel peaks and the incident neutron wavelength distribution. Another important parameter of the data is the elastic incoherent structure factor (EISF) which is defined as the ratio of the integrated elastic intensity to the total scattering intensity; this parameter determines I(Q, t) at long times. At T = 30 K, the oscillatory part of the intermediate scattering function completely disappears, and I(Q, t) can be described by a monotonically decaying function of time. Such a behavior reflects a gradual transition from the low-temperature rotational tunneling to the regime of classical reorientational jumps at higher temperatures.

Figure 6.

NSE intensity at Q = 1.65 Å as a function of the Fourier time for Li₂(bIm)¹¹BH₄ at 3.6, 20, and 30 K. For the lowest two temperatures, the solid lines show model fits assuming the existence of Gaussian-shaped tunneling peaks in S(Q, ω) space, whereas for 30 K, the solid line shows the model fit for purely exponential decay of I(Q, t) associated with a single Lorentzian-shaped quasi-elastic line broadening in S(Q, ω) space.

For parametrization of the two lower-temperature NSE results, we have used the model with two Gaussian-broadened tunneling peaks, both with fwhm linewidths w, centered at ±ℏω_t. The results of the fits taking into account a Gaussian-shaped incident neutron wavelength distribution are shown as solid lines in Figure 6. The corresponding fit parameters are ℏω_t = 0.43(2) μeV, w = 0.18(7) μeV and EISF = 0.82(1) at 3.6 K, and ℏω_t = 0.34(5) μeV, w = 0.66(4) μeV and EISF = 0.71(2) at 20 K. It should be noted that the low-temperature value of the tunnel splitting appears to be close to that derived from NMR. With increasing temperature, the splitting ℏω_t is found to decrease, while the width w becomes larger. Such a behavior is typical of systems with the rotational tunneling,^9,10 where the tunnel peaks gradually merge into the central line at higher temperatures.

At 30 K, the NSE data can be reasonably fitted by the model with a single quasi-elastic line with w = 0.51(7) μeV and EISF = 0.67(2), consistent with the expected gradual transformation from quantum rotational tunneling to classical stochastic jump reorientations.⁹

The observation of a single tunnel splitting of 0.43(2) μeV is consistent with the rotational tunneling occurring preferentially among three H atoms around a single 3-fold BH₄⁻ anion symmetry axis, rather than among all four tetrahedrally distributed H atoms, which would display additional tunneling lines as observed for other tetrahedrally symmetric rotors.^9,10 Of course, the present result is expected and fully consistent with the unusual BH₄⁻ coordination to the Li₄ cluster shown in Figure 1. More subtle details concerning the relationship between the neutron spin echo and neutron vibrational spectroscopy data are discussed in the Supporting Information.

Neutron Backscattering Spectroscopy (Low Temperatures).

Although the roughly 1 μeV instrumental resolution of HFBS makes it difficult to observe the submicrovolt BH₄⁻ rotational tunneling lines in Li₂(bIm)BH₄, they are nonetheless still evident as minor shoulders on the 1.5 K elastic scattering peak shown in Figure 7. Missing tunneling features are clearly manifested by the difference spectrum (fit-data) when only a resolution function and flat background are considered in the fitting procedure (see Figure 7a). Since the tunneling features are largely buried under the elastic peak, simultaneous fitting of their position, width, and intensities becomes problematic. For example, if a delta function is assumed for the two tunneling lines, then the observed intensities are lower than expected, and the value of the splitting is higher than expected. Figure 7b shows a typical fit to the data using the NSE results by fixing the tunnel splitting at ±0.43 μeV and assuming Gaussian-broadened lineshapes, both with linewidths of 0.18 μeV fwhm.

Figure 7.

HFBS data for Li₂(bIm)¹¹BH₄ at 1.5 K fitted with a resolution-broadened delta function and flat background (a) without and (b) with a pair of 0.18 μeV fwhm, Gaussian-shaped, tunneling lines at ±0.43 μeV. (c) HFBS data for Li₂(bIm)¹¹BH₄ at 35 K fitted with a sum of resolution-broadened delta and Lorentzian functions and flat background. Residual differences are plotted beneath the fitted spectra. Insets enlarge the region between ±2 μeV.

Figure 7c shows the transformation from quantum tunneling behavior (discrete tunneling peaks) toward classical stochastic 3-fold jump reorientations (quasi-elastic-like Lorentzian broadening) upon increasing the temperature from 1.5 to 35 K. Above 30 K, the QENS spectra could be adequately described by a delta function and a single Lorentzian component, both convoluted with the resolution function, above a flat background. The Lorentzian fwhm line width Γ was found to remain constant as a function of Q.

The temperature dependence of Γ in the range between 32 and 45 K can be satisfactorily approximated by the Arrhenius-type expression with the activation energy of 17.2(2) meV. The corresponding results are shown in Figure 8. This figure includes our data on the jump correlation frequencies obtained from various QENS and NMR experiments versus inverse temperature. For hydrogen reorientational jumps around the anchored B–H bond axis, the fundamental jump correlation frequency τ₁⁻¹ is proportional to Γ, τ₁⁻¹ = Γ/(2ℏ). This correlation frequency is expected to be equivalent to τ⁻¹ derived from NMR experiments. Indeed, as can be seen from Figure 8, the HFBS results in the range 32–45 K are close to the NSE result at 30 K and to the points obtained from the low-T proton spin–lattice relaxation rate maxima.

Figure 8.

Arrhenius-type plots of the jump correlation frequencies obtained from various QENS and NMR experiments versus inverse temperature. Red symbols: points derived from the proton spin–lattice relaxation rate maxima at different resonance frequencies. Blue symbol: neutron spin echo result at 30 K. Green symbols: time-of-flight QENS results (DCS). Black symbols: backscattering QENS results (HFBS) for both the fast and slow jump processes. The inset shows the enlarged view of the HFBS results for the slow jump process. Solid red lines represent the fits of the proton spin–lattice relaxation results for the fast and slow processes. The solid black line represents the Arrhenius fit to the HFBS for the slow process. Dashed black and green lines show the Arrhenius fits to the HFBS and DCS data, respectively, for the fast process.

Neutron Time-of-Flight Spectroscopy.

To follow the fast BH₄⁻ reorientational motion to even higher temperatures, QENS spectra were collected on the time-of-flight neutron spectrometer DCS between 42 and 153 K. A representative spectrum is shown in Figure S11 of the Supporting Information. As for the lower-temperature HFBS spectra, all DCS spectra could be adequately approximated by a delta function and a single Lorentzian component, both convoluted with the resolution function, above a flat background. Again, the Lorentzian line width Γ was found to be Q-independent. The corresponding jump correlation frequencies resulting from the DCS spectra are included in Figure 8; the activation energy derived from this Arrhenius-like dependence is 18.0(2) meV. Although this activation energy appears to be close to that obtained from the HFBS data between 32 and 45 K, the actual Γ values derived from the DCS spectra are considerably higher than those derived from the HFBS spectra in the temperature range of partial overlap of the data. A possible reason for this discrepancy may be related to subtle structural changes observed between 35 and 50 K (see Figures S2–S4, and S7 of the Supporting Information). In particular, Figure S7 indicates a relatively sharp change in lattice distortion in this temperature region, which may ultimately affect the −BH₃ rotational potential profile, resulting in further enhancement in reorientational mobility at higher temperatures. Note that the collapse of the −BH₃ librational bands with increasing temperature in Figure 2 reflects the effects of the increasingly rapid reorientational motions that are measured on DCS. Besides invoking the structural-change arguments above, another possible reason may be related to the presence of a distribution of the reorientational jump rates. As discussed previously,³⁹ in the presence of broad jump rate distributions, the standard analysis of QENS spectra is expected to underestimate the changes in the quasi-elastic line width with temperature.

To discuss the nature of the reorientational mechanism, we have to compare the experimental Q dependence of the elastic incoherent structure factor (EISF) with its calculated behavior for different possible models. For such a comparison, it is preferable to use the data at a short incident neutron wavelength, since these data allow us to access a broader Q range.

Figure 9 shows the Q dependence of the EISF for Li₂(bIm)¹¹BH₄ at 80 K derived from the DCS data using the incident neutron wavelength of 2.75 Å. It should be noted that the EISF results shown in Figure 9 correspond to the contribution solely due to BH₄⁻ anions, i.e., after removing the extra elastic scattering contributions from the “immobile” H atoms associated with benzimidazolate anions both in the main compound and in the minor Li(bIm) impurity (see Figure S1 of the Supporting Information). The orange curve in Figure 9 shows the model Q dependence of the EISF for uniaxial 3-fold jumps of BH₄⁻ anions around the anchored B–H bond C₃ axis⁴⁰

$${\text{EISF}}_{C_3}=\frac{1}{2}\left[1+j_0(Qd)\right]$$ (4)

where j₀(x) is the zeroth-order spherical Bessel function equal to sin(x)/x, and d ≈ 2.0 Å is the jump distance between two H atoms in BH₄⁻. It can be seen that the agreement between the experimental data up to Q ≈ 4.2 Å⁻¹ and this 3-fold model is satisfactory. The alternative models include the uniaxial rotational diffusion around the anchored bond axis, which in the measured Q range can be well-approximated by considering 6-fold reorientations⁴¹

$${\text{EISF}}_{\text{rot}.\text{diff}.}=\frac{1}{8}[3+2j_0(Qd/\sqrt{3})+2j_0(Qd)+j_0(2Qd/\sqrt{3})]$$ (5)

and tetrahedral tumbling of BH₄⁻ anions, which allows all associated hydrogen atoms to visit any of the four crystallographic H positions of the anion⁴⁰

$${\text{EISF}}_{\text{tetr}.}=\frac{1}{4}\left[1+3j_0(Qd)\right]$$ (6)

As can be seen from Figure 9, both the models of uniaxial rotational diffusion and the tetrahedral tumbling do not provide a reasonable description of the experimental results. It should be noted that, for the tetrahedral BH₄⁻ anion, the uniaxial C₃ model (with one immobile hydrogen atom) happens to exhibit the same Q dependence of the EISF as the model of uniaxial 180° (2-fold) reorientations around one of the C₂ symmetry axes (with no immobile hydrogen atoms). Both C₃ and C₂-type jump models are also consistent with the observed Q-independence of QENS linewidths Γ.^42,43 Yet, based on the crystallographic structure and nature of the anion rotational potential, we can confidently discount this latter 2-fold jump mechanism. Hence, the observed EISF behavior corroborates the expected 3-fold jump mechanism of the anchored−BH₃ fragments and indicates that, even at 80 K, they still undergo reorientational jumps between discrete 3-fold potential wells spaced 120° apart. This makes sense if most BH₄⁻ anions are still in their librational ground state at this temperature. At such a low temperature, it is enough to approximate the BH₄⁻ librational potential comprised of only two levels, i.e., the ground-state and first-excited-state levels. In this instance, the fraction of BH₄⁻ anions populating the ground-state level is given by the Fermi–Dirac distribution relation (1 + exp(–E₀₁/(k_BT))⁻¹. At 80 K and an assumed librational excitation energy E₀₁ of 13.3 meV, this ground-state fraction is indeed an overwhelming 87%.

Figure 9.

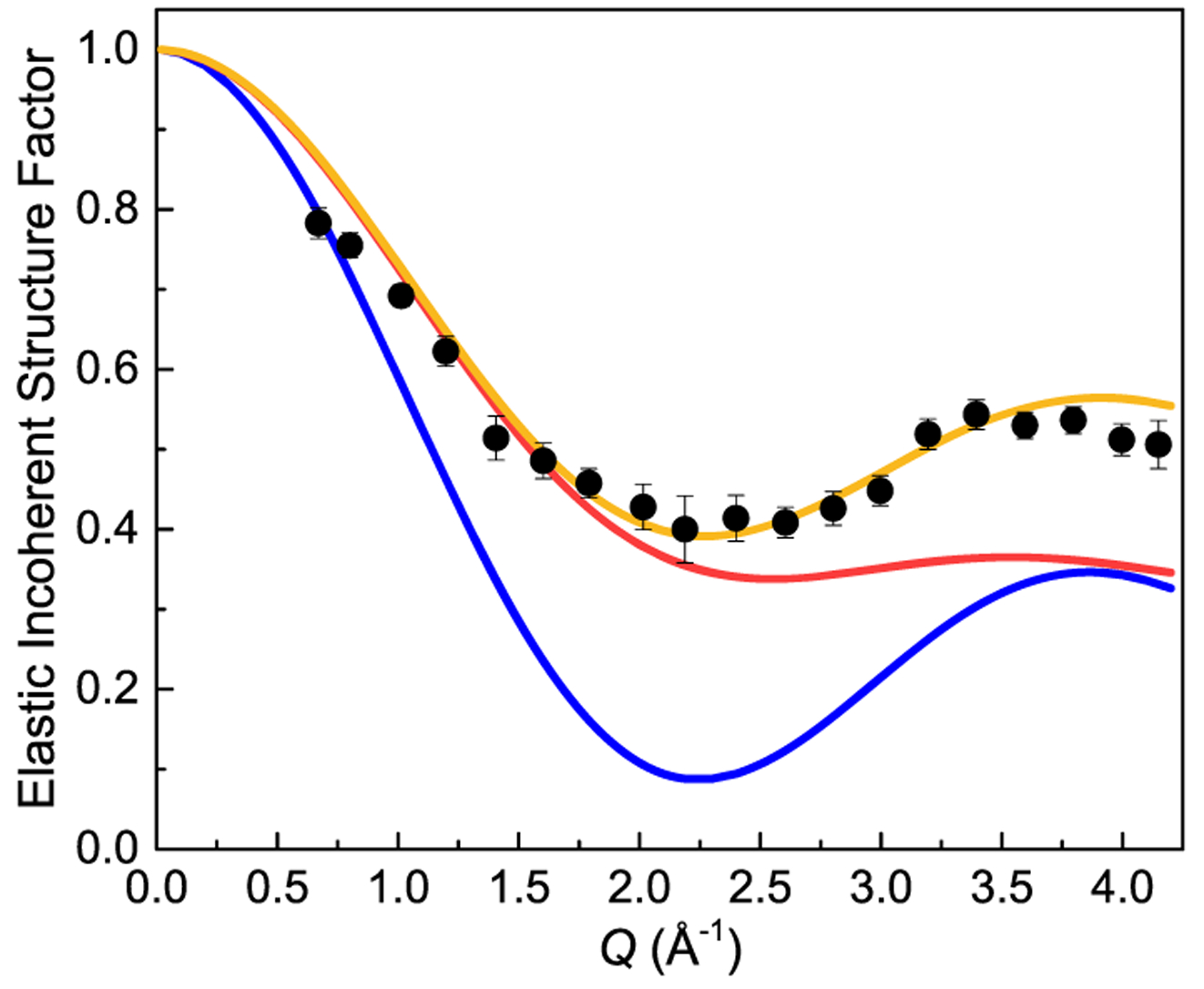
Elastic incoherent structure factor for BH₄⁻ anions in Li₂(bIm)¹¹BH₄ as a function of Q. The experimental points (black circles) are determined from the DCS data (using the incident neutron wavelength of 2.75 Å) at 80 K. The curves represent the model of uniaxial 3-fold jumps of BH₄⁻ anions around the anchored B–H bond C₃ axis (orange), the model of uniaxial rotational diffusion around the C₃ axis (red), and the model of BH₄⁻ tetrahedral tumbling (blue).

Neutron Backscattering Spectroscopy (High Temperatures).

To probe the slower reorientational process (responsible for the high-temperature $R_1^{\text{H}}(T)$ peak), we have performed neutron backscattering measurements up to 385 K. Figure 10 shows the HFBS neutron-elastic-scattering fixed-window scan (FWS) in heating from 4 to 385 K. The FWS reflects the temperature dependence of the neutron scattering intensity at zero-energy transfer. Between 4 and 25 K, the FWS intensity remains nearly constant as the tunneling peaks gradually collapse and broaden toward zero energy. At higher temperatures, the FWS intensity starts to fall sharply, since the classical quasi-elastic line broadening leads to a loss of zero-energy intensity. By about 40 K, the H jump rates reach ~10¹⁰ s⁻¹, beginning to move outside the HFBS energy window. This is expected to lead to a certain leveling-off of the FWS intensity. However, the experimental FWS intensity continues to fall noticeably all the way up to 385 K due to the relatively large Debye–Waller factor associated with the three librating H atoms of the BH₄⁻ anions around the anchored B–H bond axis.

Figure 10.

Results of the neutron-elastic scattering fixed-window scan on HFBS for Li₂(bIm)¹¹BH₄ upon heating at a rate of 1 K/min from 4 to 385 K at Q = 1.2 Å⁻¹.

Between ~280 and 350 K, an additional minor intensity drop is also evident, which indicates the onset of a second reorientational jump process, presumably due to another type of BH₄⁻ reorientational motion according to the NMR results, at the frequency scale of the HFBS.

Additional QENS measurements were made on HFBS between 300 and 385 K to characterize the H jump rates and activation energy corresponding to this slower BH₄⁻ reorientational process. Again, the QENS spectra could be adequately fit with a delta function and a single Lorentzian component, both convoluted with the resolution function, above a flat background (see Figure S12 in the Supporting Information). Moreover, the quasi-elastic line width appeared to be Q-independent over the limited Q range accessed. The resulting values of H jump rates are shown in Figure 8; their temperature dependence in the range 300–385 K is well-described by the Arrhenius law with the fitted reorientation barrier of 261(1) meV. This value is identical to the activation energy of 261(4) meV determined from the NMR data for the slower reorientational process. It is reasonable to assume that the slower process corresponds to the reorientational exchange between the anchored H atom of the BH₄⁻ anion and one of the rapidly rotating H atoms in the −BH₃ fragment. This type of composite reorientational mechanism was also observed for BH₄⁻ in both hexagonal LiBH₄ (ref 44) and hexagonal LiBH₄-LiI solid solution phases.⁴¹ No further effort was made to extract a composite EISF from the HFBS data since we would need an accurate assessment of the Q-dependent quasi-elastic scattering intensity from the rapidly reorienting −BH₃ rotor, which is essentially hidden as part of the flat background and extends orders of magnitude outside the energy range of the instrument.

CONCLUSIONS

Our nuclear magnetic resonance and quasi-elastic neutron scattering experiments have revealed the exceptionally fast low-temperature reorientational motion of BH₄⁻ anions in lithium benzimidazolate-borohydride Li2(bIm)BH4. This motion is facilitated by the unusual coordination of tetrahydroborate groups in Li2(bIm)BH4: each BH₄⁻ anion has one of its H atoms anchored within a nearly square hollow formed by four coplanar Li+ cations, while the remaining −BH3 fragment extends into a relatively open space, being only loosely coordinated to other atoms. As a result, the energy barriers for reorientations of this fragment around the anchored B–H bond axis appear to be very small. At low temperatures, this uniaxial motion can be described as rotational tunneling. According to the neutron spin echo results, the tunnel splitting at 3.6 K is 0.43(2) μeV. To the best of our knowledge, this is the first well-documented case of rotational tunneling for BH4 groups. As the temperature increases from 3.6 to ~30 K, we observe a gradual transition from the regime of low-temperature quantum dynamics (rotational tunneling) to the regime of classical thermally activated jump reorientations. According to the neutron time-of-flight spectroscopy results, the reorientational jump rate reaches 5 × 1011 s−1 at 80 K. Measurements of the elastic incoherent structure factor at this temperature are consistent with the model of uniaxial 3-fold reorientations of the tetrahydroborate groups. Nearer room temperature and above, both NMR and QENS measurements have revealed a second BH₄⁻ reorientational process characterized by the activation energy of 261 meV. This process is several orders of magnitude slower than the uniaxial 3-fold reorientations; presumably, it corresponds to exchanges between the anchored H atom and the other three rapidly reorienting H atoms of the −BH3 fragment.