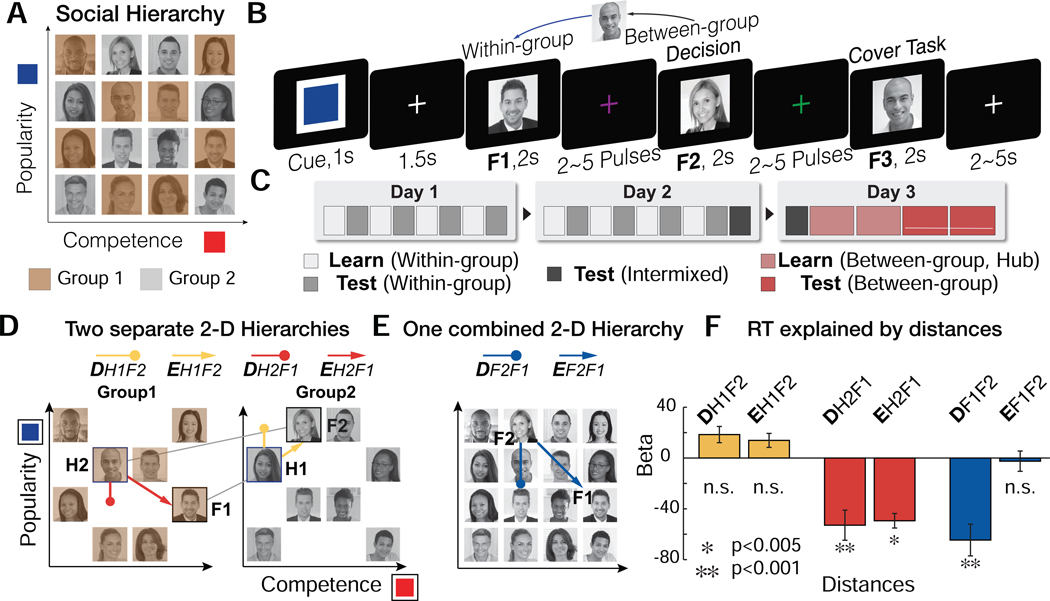
Figure 2.

A. Participants learned the rank of members of each of two groups (brown and gray) separately in two dimensions: competence and popularity. Subjects were never shown the 1- or 2-D structures. B. Illustration of a trial of the fMRI experiment. Participants made inferences about the relative status of a novel pair (F1 and F2) in a given dimension (signaled by the Cue color). A cover task (to indicate the gender of the face stimulus, F3) followed at the end of every trial. C. On day 1 and day 2, participants learned within-group ranks of the two groups in each of two dimensions through binary decisions about the status of members who differed by only one rank level in a given dimension. On day3, subjects learned from between-group comparisons limited to ‘hub’ individuals, which created a unique path between groups per person in each dimension. Subsequently, on day3, participants were asked to infer the unlearned between-group status while undergoing fMRI. D. Participants could use hubs to infer the relationship between novel pairs. Possible trajectories for example inferences can be shown for each trajectory: the behaviorally-relevant 1-D distance (D, Fig.1C) and the 2-D Euclidean distance (E, Fig.1D). Subjects could use either of two trajectories: a forward inference from F1 to its hub (H1) that has a unique connection to F2 (D_H1F2, E_H1F2; yellow); or a backward inference from F2 to its hub (H2) that has a unique connection to F1 (D_H2F1, E_H2F1; red). E. As alternative paths, subjects may not use the hubs, but instead compute the distance in the relevant dimension between F1 and F2 directly (D_F1F2), or their Euclidean distance (E_F1F2) in the combined cognitive map of two groups (blue). F. Multiple linear regression results show that both the rank distance (D_H2F1) and the Euclidean distance from H2 (E_H2F1), but not from H1, significantly explain variance in RTs, in addition to the direct distance between F1 and F2 (D_F1F2), while competing with other distance terms.