FIG. 5.

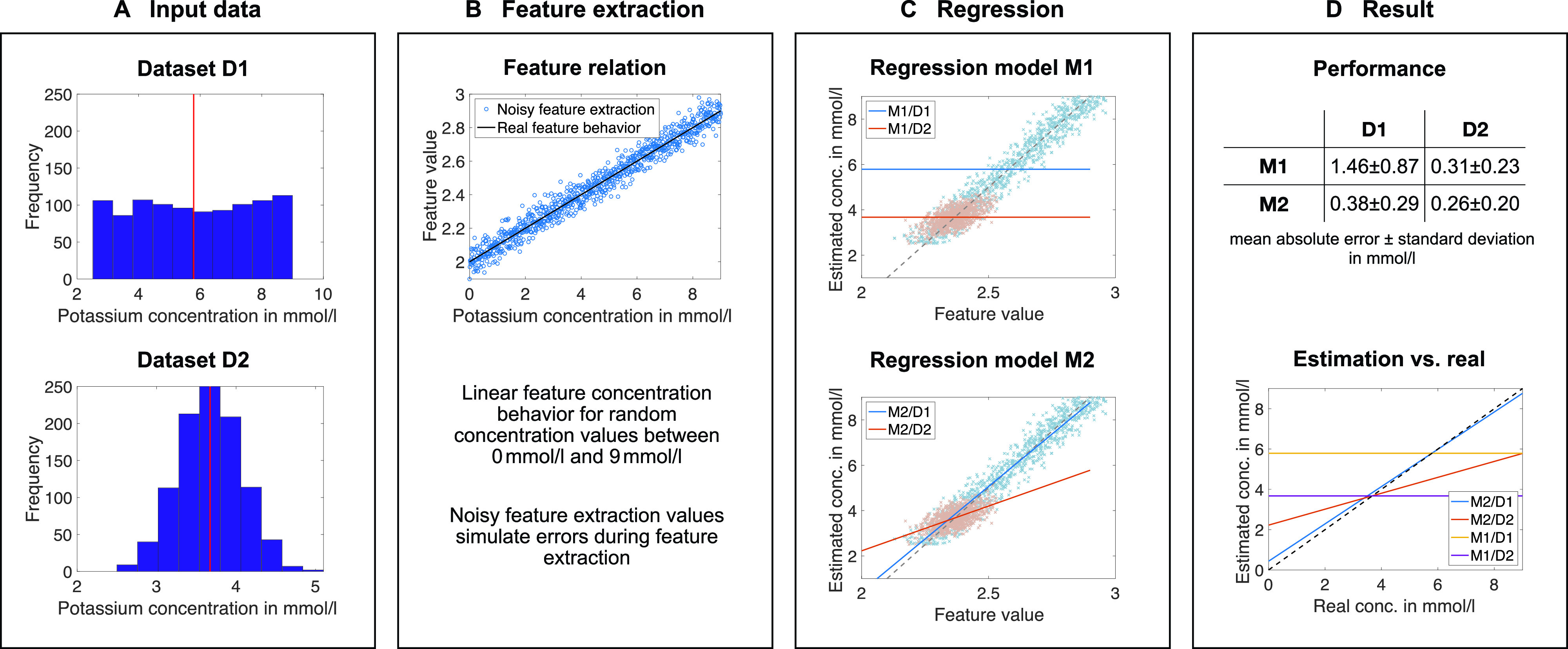
An example to illustrate the problem of using mean and standard deviation as sole performance parameters. (a) Two exemplary datasets D1 and D2 with a uniform and normal distribution, respectively. (b) An exemplary linear feature concentration dependence. For the subsequent fitting, feature values were randomly distorted by up to 5.5%. (c) The result of two regression methods. Method M1 is a fit with a constant minimizing the error, and model M2 is a linear fit in the least squares sense. The light red (dataset D2) and light blue (dataset D1) point clouds visualize the noisy feature inputs for the fitting yielding the models in red and blue, respectively. The dashed line is the real noise-free relation. (d) Results of both methods on both datasets. Although the combination of M2/D1 reconstructs the underlying dependency over the whole interval best, it is outperformed by the combination M2/D2 and M1/D2 when considering the mean absolute error. Within a dataset, the linear model (M2) always outperforms the constant (M1) as expected.