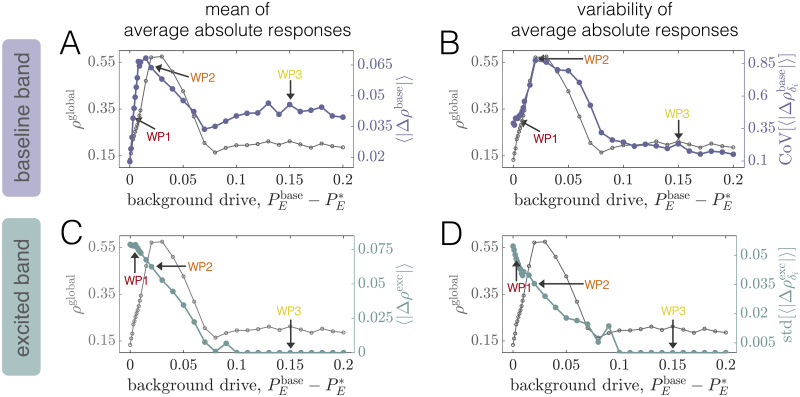
Fig 8. Dependence of global phase-locking changes on the baseline state of the brain network model.

(A) The left axis (gray) shows the network-averaged baseline PLV ρ^global as a function of background drive $P_E^{\text{base}}-P_E^{*}$ for a coupling C = 2.5. The right axis (purple) shows the grand average 〈|Δρ^base|〉 of the perturbation-induced absolute changes in baseline band PLVs as a function of $P_E^{\text{base}}-P_E^{*}$. (B) The left axis (gray) shows the network-averaged baseline PLV ρ^global as a function of background drive $P_E^{\text{base}}-P_E^{*}$ for a coupling C = 2.5. The right axis (purple) shows the coefficient of variation of the perturbation-induced average absolute changes in baseline band PLVs, $\text{CoV}[\langle |\Delta {\rho }_{{\delta }_i}^{\text{base}}|\rangle ]$, as a function of $P_E^{\text{base}}-P_E^{*}$. (C) The left axis (gray) shows the network-averaged baseline PLV ρ^global as a function of background drive $P_E^{\text{base}}-P_E^{*}$ for a coupling C = 2.5. The right axis (green) shows the grand average 〈|Δρ^exc|〉 of the perturbation-induced absolute changes in excited band PLVs as a function of $P_E^{\text{base}}-P_E^{*}$. (D) The left axis (gray) shows the network-averaged baseline PLV ρ^global as a function of background drive $P_E^{\text{base}}-P_E^{*}$ for a coupling C = 2.5. The right axis (green) shows the standard deviation of the perturbation-induced average absolute changes in excited band PLVs, $\text{std}[\langle |\Delta {\rho }_{{\delta }_i}^{\text{exc}}|\rangle ]$, as a function of $P_E^{\text{base}}-P_E^{*}$. (Note that here we consider the standard deviation rather than the coefficient of variation since the mean response in the excited band eventually drops to zero.).