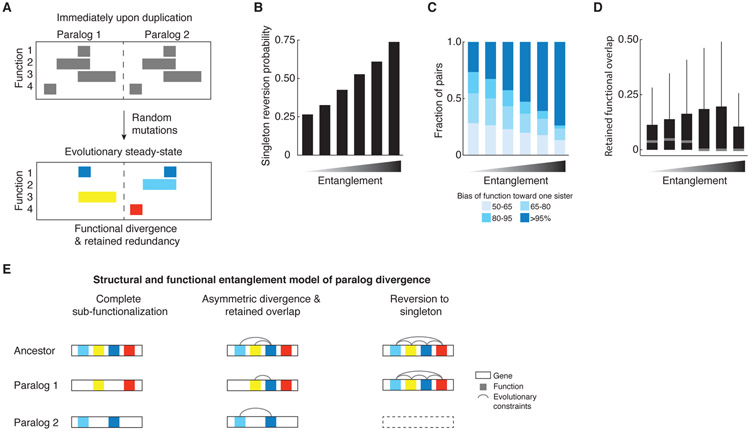
Fig. 7. In silico evolutionary model.

(A) Schematic depiction of the in silico evolutionary model. The pair evolves through random mutations until it reaches an evolutionarily stable-state that can sustain no further mutations without a loss of function. Top panel shows a pair at the start of the evolutionary trajectory and bottom panel shows a pair that achieves a division of labor with a retention of a common function (dark blue blocks), the loss of which is prevented because it would compromise the unique functions of each paralog (yellow, light blue, red). (B-D) Evolutionary fates of paralogs with functional and structural entanglement. Paralogs were generated to represent a range of overlapping functional domains at the onset of their evolutionary trajectory and the propensity to assume specific paralog properties was quantified. In each case, x-axis represents bins of initial functional overlap as a fraction of “gene” length at the start of the simulations (< 10%, 30%, 50%, 70%, 90%, 100%, respectively); y-axis depicts the propensities of paralogs to (B) revert to a singleton state, (C) evolve functional asymmetry, (D) retain functional overlap at the evolutionary steady-state. (E) The structural and functional entanglement model of paralog divergence. A pair will evolve by sub-functionalization, if it is modular and is composed of partitionable functions (left). A paralog pair that is very structurally and functionally entangled will have a high probability of reversion to a singleton state since one of the sisters will quickly degenerate (right). Paralogs with an intermediate level of entanglement at the time of duplication will tend to partition some and retain some overlapping functions, allowing for specialization of a common activity (middle).