Photocurrent detection of the orbital angular momentum of light

Abstract

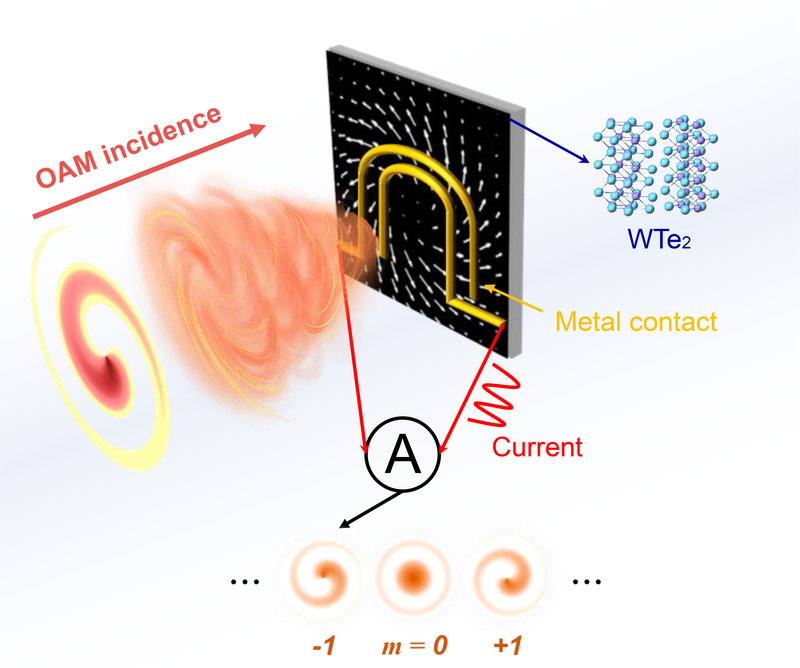
Applications that use the orbital angular momentum (OAM) of light show promise for increasing the bandwidth of optical communication networks. However, direct photocurrent detection of different OAM modes has not yet been demonstrated. Most studies of current responses to electromagnetic fields have focused on optical intensity–related effects, but phase information has been lost. In this study, we designed a photodetector based on tungsten ditelluride (WTe2) with carefully fabricated electrode geometries to facilitate direct characterization of the topological charge of OAM of light. This orbital photogalvanic effect, driven by the helical phase gradient, is distinguished by a current winding around the optical beam axis with a magnitude proportional to its quantized OAM mode number. Our study provides a route to develop on-chip detection of optical OAM modes, which can enable the development of next-generation photonic circuits.

The interaction between the oscillating electromagnetic field of light and the electric or magnetic dipole moment of matter can be designed to go beyond simple intensity and temporal characteristics by manipulating light’s different degrees of freedom (e.g., frequency, polarization, phase, and angular momentum). One such property is the spin angular momentum (SAM) of light, which can induce a linear motion of electrons to generate dc photocurrent that switches with light helicity. This circular photogalvanic effect (1–3) is governed by angular momentum conservation laws and is a powerful technique for exploring the interaction between the chiral degree of freedom of matter and SAM of light.

In addition to spin, light can also carry an orbital angular momentum (OAM) (4, 5). Whereas SAM of light is associated with its polarization state and has a bounded value S = ±ℏ per photon, OAM is also quantized but unbounded, given by L = mℏ (m is the mode number and ℏ is Planck’s constant divided by 2π). OAM of light leads to a spatial distribution of the phase of the optical field, which manifests as a helical wavefront or an azimuthal phase dependence e^imϕ (where ϕ is the azimuthal angle). Exploiting the OAM modes of light has been widely proposed to enable the next generation of high-capacity photonics, but direct electrical readout of OAM is a challenge, thus limiting its applications towards system-level integrations that require on-chip generation (6, 7), waveguiding (8), to detection (9,10) of OAM.

Extensive theoretical (11–13) and some experimental studies have reported on the interaction between OAM of light and atomic media (14, 15), generating new selection rules and optical responses. These studies suggest that the optical phase gradient modifies the excitation processes, but the results cannot be translated to obtain direct photocurrent generation for fabricating OAM-sensitive photodetectors. This is because dc photocurrent response does not inherently carry phase information, and the slow variation of vector potential associated with OAM of light compared to the Brillouin zone size limits its influence on microscopic processes (16). Here we show that OAM of light can induce a strong, nonlocal interaction between electromagnetic waves and matter. Additionally, we discuss our observation of a distinctive photocurrent from OAM emerging from the phase gradient of optical fields, the direction and amplitude of which directly reflect the different OAM modes (Fig. 1).

Figure 1:

Schematic of the photocurrent measurement from optical beams carrying OAM.

The in-plane electric field of a monochromatic, Laguerre-Gaussian $({\text{LG}}_0^{\text{m}})$ beam with OAM order m propagating in the $\widehat{\mathit{z}}$-direction is given by (17),

$$\mathit{E}(\mathit{r},t)=u(\rho ,z)e^{im\varphi }{e}^{i\left(k_{z}z-\omega t\right)}\widehat{\mathit{ϵ}}+c.c.$$ (1)

under the paraxial approximation, where r = (ρ, ϕ, z) is the position in the cylindrical coordinate, u(ρ, z) is the donut-shaped LG mode profile, $k_z\widehat{\mathit{z}}$ is the wave vector, ω is the frequency, t is time, c.c. is the complex conjugate, and polarization of light is determined by $\widehat{\mathit{ϵ}}=(\widehat{\mathit{x}}+i\sigma \widehat{\mathit{y}})$, with σ being the optical helicity (−1 < σ < 1) or SAM of the beam. The electric field can be Fourier expanded as $\mathit{E}(\mathit{r},\omega )=1/{(2\pi )}^3\int d\mathit{q}\mathit{E}(\mathit{q},\omega )e^{i\mathit{q}\cdot \mathit{r}}$. When the OAM order m is nonzero, besides $\mathit{k}=k_z\widehat{\mathit{z}}$, an ‘azimuthal photon momentum’ q_φ also arises from the helical phase ϕ. Then, a general second order dc response from the interaction of E(q, ω) and E(−q, −ω), by accounting for the helical phase is (Supplementary material section S1.1 to S1.4)

$$\begin{gathered} j_k^{(dc)}(\mathit{r},t)={\iint \frac{d\mathit{q}d(-\mathit{q})d\omega d(-\omega )}{{(2\pi )}^8}{\xi }_{ijk}(\mathit{q},\omega ;-\mathit{q},-\omega )E_i(\mathit{q},\omega )E_j(-\mathit{q},-\omega )e^{-i(\omega -\omega )t}{e}^{i(\mathit{q}-\mathit{q})\cdot \mathit{r}}|}_{\mathit{q}=q_{\varphi }\mathit{\varphi }} \\ \approx {\alpha }_{ijk}(\omega ,-\omega )E_i(\mathit{r},\omega )E_j(\mathit{r},-\omega )+{\mathrm{\beta }}_{ijkl}(\omega ,-\omega ){\nabla }_l{E}_i(\mathit{r},\omega )E_j(\mathit{r},-\omega ) \end{gathered}$$ (2)

where the subscripts i, j, k and l stand for directions in the cylindrical coordinate system, and at normal incidence, the summations of i, j and k are over in-plane components (i.e., ρ and ϕ). In the small perturbation limit (q is ~10⁻³ times smaller than Brillouin zone length), the second order conductivity tensor can be expanded up to the first order of q to obtain, ${\xi }_{ijk}(\mathit{q},\omega ;-\mathit{q},-\omega )\approx {\alpha }_{ijk}+i{q}_l{\beta }_{ijkl}.{\alpha }_{ijk}$ corresponds to the conventional photogalvanic conductivity tensor, which implies that in the small q limit OAM of light does not appreciably change the dipole selection rules, and hence the local current response to light field will be determined by its local intensity and polarization, regardless of the OAM order. It explains the absence of signatures of OAM transfer to matter in photoemission experiments (16), and further suggests that when the lowest order α_ijk tensor exists, as in previous high harmonic generation studies (18), OAM carrying optical beams are almost equivalent to plane waves (since α_ijk is unchanged), except for modifying the phase factors under phase-matching conditions. However, the conductivity tensor, β_ijkl, goes beyond the dipole-approximation and describes a part of spatially nonlocal current proportional to the helical phase gradient, and hence the OAM of light-induced photocurrent can be obtained as (Supplementary materials section S1.3)

$$J_k(\rho ,\varphi )={\beta }_{ijk\varphi }(\omega ,-\omega )\frac{1}{2}\left[{\nabla }_{\mathrm{\varphi }}{E}_i(\mathit{r},\omega )E_j(\mathit{r},-\omega )-{\nabla }_{\mathrm{\varphi }}{E}_j(\mathit{r},-\omega )E_i(\mathit{r},\omega )\right]\propto m$$ (3)

The gradient operator ∇_ϕ in Eq. (3) directly corresponds to the helical phase gradient in the ϕ direction and is a signature of the nonlocality of the photocurrent. β_ijkl can also be divided into a symmetric $({\beta }_{ijkl}^{+}=({\beta }_{ijkl}+{\beta }_{jikl})/2)$ part dependent on linear polarization and an antisymmetric $({\beta }_{ijkl}^{-}=({\beta }_{ijkl}-{\beta }_{jikl})/2)$ part that switches with light helicity. Therefore, the phase information of OAM of light is maintained in the nonlocal, polarization-dependent photocurrent J_k, and forms the central hypothesis of our studies.

${\text{LG}}_0^m$ modes (Figs. 1 and 2) were obtained by modulating a linearly-polarized collimated light beam from a Ti-sapphire laser (wavelength: 1 μm) with a phase-only spatial light modulator (SLM). The beam was then transmitted through a quarter waveplate (QWP) and focused by a 60× objective to a spot size of ~3 to 20 μm, and the sample was irradiated at normal incidence (19). To measure the response from OAM of light, a material system with symmetry-forbidden photogalvanic response (described by $\overleftrightarrow{\alpha }$) under normal incidence, but supporting the nonlocal response (described by $\overleftrightarrow{\beta }$) when the helical phase gradient breaks certain in-plane symmetries is desired. The material chosen in our study is ~50- to 200-nm-thick exfoliated single-crystalline WTe₂ in T_d phase (Pmn2₁), a type-II Weyl semimetal (20) with large nonlinear optical susceptibilities (21, 22) and a symmetry-forbidding contribution from tensor α under normal incidence (along c-axis). In the laboratory cylindrical coordinate (ρ, ϕ, z) frame, measurable terms related to the nonlocal current and response to light helicity include ${\beta }_{\rho \varphi \rho \varphi }^{-}$ and ${\beta }_{\rho \varphi \varphi \varphi }^{-}$, which correspond to photocurrents along radial $\left(\widehat{\mathit{\rho }}\right)$ and azimuthal $(\widehat{\mathit{\varphi }})$ directions, respectively (Supplementary material section S1.3).

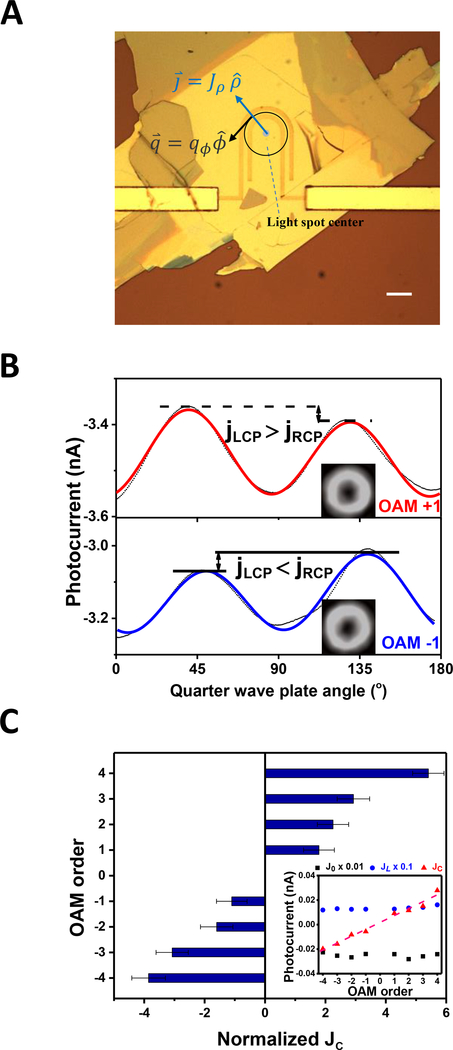
Figure 2: Evidence of the nonlocal photocurrent generated by OAM of light and its dependence on OAM order.

(A) Optical image of a photodetector device with ‘U’-shaped electrodes on WTe2. The light spot is focused at the center of the arc defined by the electrodes (blue circle).. Scale bar: 10 μm. (B) Measured photocurrent amplitudes from OAM +1 (red curve) and −1 (blue curve) beams, as a function of the QWP angle (α). The insets are CCD images of OAM +1 and −1 beams. (C) Normalized photocurrent that switches with circular polarization, from beams with OAM order ranging from −4 to 4. Error bars represent the standard deviations of the fitting. (Inset) Three components of the measured photocurrent: J₀, J_L and J_C.

To identify and characterize photocurrent response from the helical phase profile of the optical beam, one must design suitable electrodes and distinguish all possible sources of current. First, since photocurrent related to the helical phase profile may flow in the radial or azimuthal directions, electrodes were designed into a U shape (Fig. 2A) to collect the radial current (see Supplementary materials sections S2.1, S2.2 for the electrostatic model and results from other electrode geometries). Second, because this current described by ${\mathrm{\beta }}_{ijkl}^{-}$ has a circular polarization dependence, the polarization of light was continuously modulated by a QWP, and the photocurrent was measured as a function of the QWP rotation angle α (Fig. 2B). In a 180° period, the light goes through linear (0°)–left circular (45°)–linear (90°)–right circular (135°) –linear (180°) polarization states. The total measured photocurrent can be divided into three parts: (i) current that switches with circular polarization with a 180°-period modulation (J_C) (23), (ii) the part sensitive to linear polarization with a 90°-period modulation (J_L) (24), and (iii) the polarization-independent component (J₀, includes thermal currents). Third, aside from the azimuthal phase profile, a LG beam also carries an annular intensity profile. As it evident from Eq. (2), it can generate spatially-dispersive photogalvanic current (J_s−PGE) proportional to the local light intensity gradient (i.e., ∂|E(ρ)|²/∂ρ) (21). Although J_s−PGE is also sensitive to light helicity, its effect can be eliminated by measuring signals from both OAM +m and −m beams because the local light intensity is preserved when OAM order reverses sign (the same argument holds for contributions from radial phase profiles; see supplementary materials section S1.4).

To first examine the existence of photocurrent from OAM of light, OAM order m = +1 and m = −1 beams generated by the SLM were measured using the ‘U’-shaped electrodes with the beam center fixed at the center of the electrode arcs (Fig. 2A). The results show that both OAM +1 and −1 beams gave rise to polarization-dependent currents (Fig. 2B). J_C from OAM +1 and OAM −1 beams have similar amplitudes but opposite polarities. By measuring the beam size and spatial dependence (Supplementary material section S2.3) and by comparing the results from various electrode geometries and mirror symmetric electrode pairs, it was further confirmed that the observed J_C did not originate from external symmetry reductions like material defects, edge effects, or beam imperfections (see supplementary materials sections S3.1 and S3.2 for details). The polarity switch of J_C cannot be attributed to spatial intensity gradients either, because the two m = ±1 beams have the same intensity profile but only differ by their helical phases (±ϕ). Therefore, these results suggest that a distinctive current – which we term the orbital photogalvanic effect (OPGE) – originates from the light OAM. OPGE is distinct from any other reported photogalvanic effects due to its nonlocal nature, spatially dispersive features, and sensitivity to the wavefront shape of light beam.

The mechanism of this photocurrent can be understood as light transferring its OAM and energy simultaneously to the electrons. Because the optical-phase varies in the azimuthal direction, it induces a spatial imbalance of excited carriers, producing a net current. This process has similarities with the photon drag effect (25, 26) (Supplementary materials section S1.3), but here the spatial variation of photon momentum plays a vital role, causing the nonlocal OPGE current to flow either along or perpendicular to the helical phase gradient. The OAM-carrying beam has a magnetic field B(ω) parallel to the beam propagation direction and through a magnetic dipole like interaction, the in-plane electric field E(−ω) and the out-of-plane magnetic field B(ω) generates a dc photocurrent, which is the OPGE current, J_OPGE ∝ E(−ω)B(ω). J_OPGE is proportional to the amplitude of the perpendicular magnetic field that changes with phase gradient, so when the OAM index reverses sign, the direction of OPGE current also flips (Fig. 2B). As noted in Eq. 3, the OPGE current can be distinctively projected onto the OAM order [when spin-orbit coupling of light (27) is not considered], with a proportionality factor dependent on the material’s conductivity tensor.

To demonstrate the discrete behavior of the OPGE current, light with OAM ±4, ±3, ±2, ±1 were generated sequentially by a phase-only SLM (with constant optical power), and the radial photocurrent was measured using the U-shaped electrode geometry with beam center fixed at the center of the electrode arcs. The measurement results (Fig. 2C) clearly show that J_C displays step-like changes from OAM order −4 to 4, in agreement with the theoretical model, which implies that the measured J_C is attributed to light helicity-sensitive OPGE current described by the conductivity tensor ${\beta }_{ijkl}^{-}$ (see Supplementary material section S2.4 for discussion of geometrical constants related to the LG profiles of different OAM orders). Our results show that when J_C is proportional to the OAM order, the linear polarization-dependent current, J_L, and the polarization-independent thermal current, J₀ do not have such dependence (Fig. 2C, inset), which indicates that they are dominated by different mechanisms (although OPGE current described by ${\beta }_{ijkl}^{+}$ is also present; Supplementary materials section S1.3, S1.4). Furthermore, since the measured OPGE current is proportional to the product of SAM and OAM, and the winding number of the light field is −m ∙ σ (13), the OPGE current thus directly characterizes the topological property of light (see Supplementary materials section S1.3, and S2.5 for generalization to mixtures of different OAM orders).

Besides scalar OAM beams, there are vectorial OAM beams with space-variant states of polarization in addition to the helical phase distribution (28). Owing to the sensitivity of OPGE on both the SAM and OAM of the optical field (Fig. 2), we studied the mechanism of photocurrent generation from these beams. Vectorial OAM beams can be represented on a higher-order Poincare sphere (HOPS) (29, 30), and the m = +1, σ = −1 HOPS is taken as an example (Fig. 3A, P1 to P5 are five representative states). In the parameter space (represented by the spherical coordinates Θ and Φ ) of the HOPS, the state of the optical field is represented by $|\mathrm{\psi }(\mathrm{\Theta },\mathrm{\Phi })\rangle =\cos (\frac{\mathrm{\Theta }}{2})\exp (-i\mathrm{\Phi }/2)|L_{-m}\rangle +\sin (\frac{\mathrm{\Theta }}{2})\exp (i\mathrm{\Phi }/2)|R_m\rangle$, where |R_m⟩ and |L_−m⟩ are scaler vortex beams with OAM +m (−m), SAM σ = −1 (σ = 1), respectively. The azimuthal OPGE current from an arbitrary state |ψ(Θ, Φ)⟩ from this HOPS can then be written as,

$$\begin{gathered} J_{\varphi ,OPGE}=J_{\varphi ,OPGE}^{(0)}+J_{\varphi ,OPGE}^{(\varphi )}= \\ {\beta }_{ij\varphi \varphi }\frac{\left({\nabla }_{\mathrm{\varphi }}{E}_i(\omega )E_j(-\omega )-{\nabla }_{\mathrm{\varphi }}{E}_j(-\omega )E_i(\omega )\right)}{2}+{\gamma }_{ij\varphi \varphi }\frac{\left({\nabla }_{\mathrm{\varphi }}{E}_i(\omega )E_j(-\omega )+{\nabla }_{\mathrm{\varphi }}{E}_j(-\omega )E_i(\omega )\right)}{2} \\ \propto \frac{m}{\rho }\left[c_0+c_1\cos (\mathrm{\Theta })+\left(c_2\cos (2(m+\sigma )\varphi +\mathrm{\Phi })+c_3\sin (2(m+\sigma )\varphi +\mathrm{\Phi })\right)\sin (\mathrm{\Theta })\right] \end{gathered}$$ (4)

where β_ijkl, γ_ijkl, c₀, c₁, c₂, c₃ are conductivity coefficients (see Supplementary materials section S2.5). At P1 and P2, the last two terms [denoted $J_{\varphi ,OPGE}^{(0)}$] vanish, and this equation reduces to Eq. (3) for scalar OAM beams.

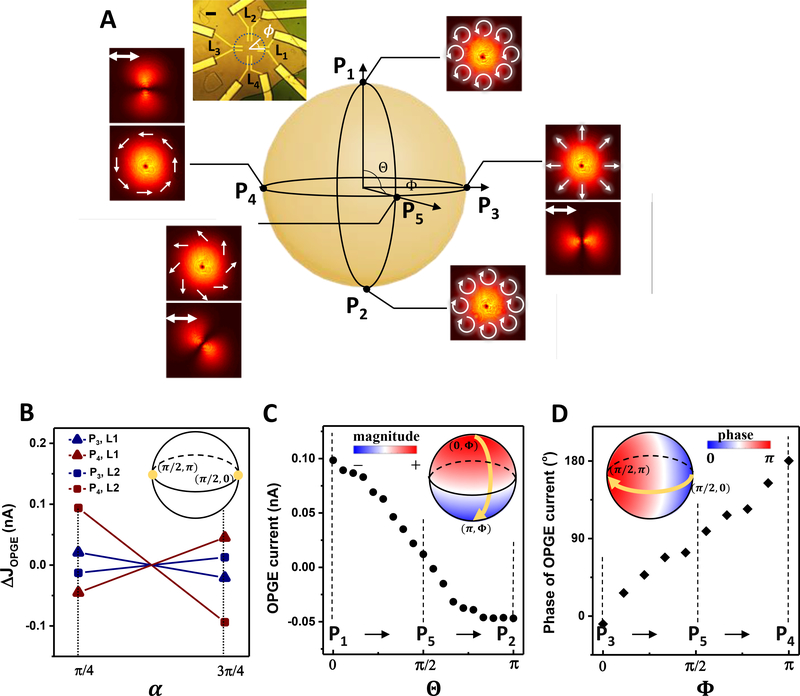
Figure 3: OPGE current from generalized vectorial OAM states on a HOPS.

(A) Schematic of the m = 1, σ = −1 HOPS, with states represented by (Θ, Φ) spherical coordinates and five points P1 to P5. Each subplot shows polarization and intensity distribution (single-headed arrows) with or without a linear polarizer oriented in the horizontal direction (double-headed arrows), and the correspondent intensity profile as recorded by a CCD camera. (Inset) Optical image of the octopus-shaped electrodes. Four pairs of electrodes (L1, L2, L3, and L4) are located at four azimuthal coordinates (ϕ = 0, $\frac{\mathrm{\pi }}{2}$, π, and 3π/2, respectively). Scale bar: 10 μm. (B) Relative photocurrent amplitudes at two angles (π/2 and 3π/2) from two states (P3 and P4) on HOPS, measured at two locations (L1 and L2). (C) OPGE current amplitude from a set of states on the line connecting P1, P5 and P2 with a same Φ. (Inset) Calculations showing a Φ-independent distribution of OPGE current. (D) Phase of OPGE current from a set of states on the line connecting P3, P5 and P4 with a fixed Θ. (Inset) Calculation showing a Θ-independent distribution of OPGE current phase.

For other points on the HOPS, $J_{OPGE}^{(\varphi )}$ described by c₂ and c₃ is, in general, non-zero, and varies with the azimuthal angle ϕ with a period of π/(m + σ) – i.e., it is determined by the total angular momentum of light. To capture this azimuthal angle dependence, the electrodes were designed into an ‘octopus’-shape (Fig. 3A, inset) to enable a set of azimuthal current measurements at various azimuthal coordinates (L1 to L4) while the beam is fixed at the center defined by the electrodes. The beam was modulated by a QWP between angles α = π/4 and 3π/4, and the amplitude variation $\Delta J_{OPGE}^{(\varphi )\prime }\propto \cos (\mathrm{\Phi }+2\varphi )$ forms an alternative signature of $J_{OPGE}^{(\varphi )}$. As shown in Fig. 3B, for both P3 and P4 states, $\Delta J_{OPGE}^{(\varphi )\prime }$ collected at different azimuthal angles L1and L2 are of opposite signs (details in Supplementary materials section S2.5), indicating the existence of $J_{OPGE}^{(\varphi )}$ that originates from the vectorial OAM beams.

To further examine the dependence of OPGE current on the (Θ, Φ) coordinates, a set of different states on the HOPS were measured. Without loss of generality, the state of vectorial OAM optical beam was swept along two lines on the sphere – from P1 to P2 with fixed Φ, and from P3 to P4 with fixed Θ (Fig. 3A) – while the photocurrent was measured at the same location (i. e., L1). As shown in Fig. 3C, when moving along the longitude on the HOPS, the OPGE current amplitude decreases from its maximum at P1 (but remains positive in the northern hemisphere), crosses zero at P5 on the equator (and then becomes negative in the southern hemisphere) and finally reaches a minimum value at P2. This result shows that the amplitude of the OPGE current has direct correspondence with Θ when Φ is fixed. On the other hand, when moving along the latitude on the Poincare sphere, the phase retardation of the OPGE current goes from 0 at point P3, π/2 at point P5, and then to π at point P4 (Fig. 3D), which indicates that the phase of the OPGE current can be mapped onto the Φ coordinate on HOPS when Θ is fixed. Therefore, our results demonstrate that different states on the HOPS have distinct OPGE photocurrent responses.

The photocurrents originating from the helical phase of the OAM-carrying beam provide evidence of the transfer of OAM to electrons and reveal the associated phase-related information in photodetection. For scalar OAM beams, the OPGE current has a direct correspondence to the topological winding number of light; for vectorial OAM beams, the variation of OPGE current with the azimuthal coordinate reflects its phase and polarization distribution simultaneously. On the basis of these results, we expect that the OAM order or the coordinates of any arbitrary OAM state on a HOPS can be specifically determined by measuring currents via a small matrix of electrodes. Once a device geometry is fixed, characterized, and calibrated, a single electrode matrix can detect a variety of OAM modes, including their arbitrary mixtures. With further optimization, on-chip detection of OAM modes of light will be possible, thus potentially facilitating OAM-based optical communication by expanding the parameter space of light.