FIGURE 3.

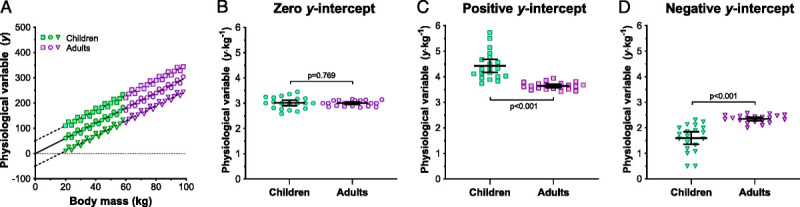
Hypothetical data to illustrate the importance of satisfying the zero y-intercept assumption when using ratiometric scaling to normalize a physiological variable (y) to body size by dividing it by an anthropometric attribute (x). Panel A shows three data sets each comprised of a physiological variable (y) that increases linearly with body size (x; body mass [kg]) in 20 children and 20 adults. The circular symbols illustrate a scenario where the y-intercept for the least-squares linear regression relationship (solid line) passes through zero and satisfies this assumption. The square and triangular symbols illustrate scenarios where that assumption is violated, with the y-intercept for this regression relationship (dashed lines) being either above or below zero, respectively. Panels B, C, and D, illustrate between-group comparisons (unpaired, two-tailed t-tests) of the ratio scaled values (y·x⁻¹) for each data set. Ratiometric scaling removed the effect of size for data which satisfy the zero y-intercept assumption (circular symbols), as indicated by a nonsignificant difference between children and adults (Panel B). In contrast, ratiometric scaling underadjusts values for children and over-adjusts values in adults when data display a positive y-intercept, and the opposite when data display a negative y-intercept. These errors result in a significant, yet artificial, between-groups difference in the ratio scaled data, but in the opposite directions (Panel C and D).