Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2020 May 5;52(11):2412–2422. doi: 10.1249/MSS.0000000000002391

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

Copyright © 2020 The Author(s). Published by Wolters Kluwer Health, Inc. on behalf of the American College of Sports Medicine.

This is an open-access article distributed under the terms of the Creative Commons Attribution-Non Commercial-No Derivatives License 4.0 (CCBY-NC-ND), where it is permissible to download and share the work provided it is properly cited. The work cannot be changed in any way or used commercially without permission from the journal.

PMC Copyright notice

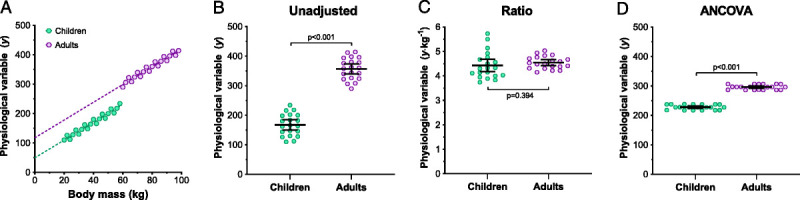
Hypothetical data to illustrate how ANCOVA (see Supplemental Digital Content 1 for procedures, http://links.lww.com/MSS/B993) can be used to account for the confounding effect of body size when data do not satisfy the zero y-intercept assumption required for ratiometric scaling. Panel A illustrates a data set comprised of a physiological variable (y) that increases linearly with body size (x; body mass [kg]) in 20 children and 20 adults, whereas the dashed lines demonstrate the least-squares linear regression relationship for each group (similar slopes). Panels B, C, and D illustrate between-group comparisons (unpaired, two-tailed t-tests) of the unadjusted, ratiometric scaled, and ANCOVA-adjusted data, respectively. Because these data display a nonzero y-intercept (panel A), ratiometric scaling cannot fully account for the effect of body size (panel C), masking the between-group difference apparent when data were normalized appropriately with ANCOVA (panel D).