Dynamics of the COVID-19 basic reproduction numbers in different countries

The reproduction number, R, is the average number of secondary infectious cases produced by one infectious case during a disease outbreak [1]. When a population is totally susceptible, R becomes the basic reproduction number, $R_0$. It is a key parameter regulating the transmission dynamics of a pandemic [2]. $R_0$ provides an indication of whether the introduction of disease will result in a localized burnout or signal the beginning of a pandemic that could move through all geographic scales [3]. The disease-free equilibrium is globally asymptotically stable and the epidemic eventually disappears if $R_0$ < 1. Whenever $R_0$ > 1, then an epidemic will occur and the infection spreads in the population, no matter how small the initial number of infected individuals. When $R_0$ > 2, a major outbreak is possible. When $R_0$ > 3, the emergence of a pandemic is generally considered to be inevitable [4].

The World Health Organization (WHO) named the corona virus disease as COVID-19 on February 11, 2020 and declared a pandemic on March 11, 2020. The basic reproduction number ($R_0$) has been employed to measure the transmission dynamics of COVID-19 both before and after the interventions. Various approaches for calculating $R_0$ for COVID-19 have been introduced, which are based on deterministic or stochastic models. Unfortunately, these results were not comparable because different algorithms for estimating $R_0$ are employed.

For instance, an algorithm based on the Susceptible-Infected-Recovered (SIR) model showed that $R_0$ monotonically rose from 0.60 on January 10 to its maximum value of 4.87 on January 25, and dropped below 1 on February 16 in Hubei Province, China [5]. A second study assumed that the epidemic curve displayed exponential growth, and the basic reproduction number for COVID-19 at the early stage, estimated in terms of the intrinsic growth rate of the epidemic curve, ranged from 2.24 to 3.58 [6]. A third study calculated an infectiousness function in terms of the average time since infection for those individuals who infect few others and those who infect many, and used the area under the curve to estimate $R_0\text{= 2.0}$ in the early stages of the epidemic in China [7]. A fourth study relied on the dominant eigenvalue of a next-generation operator [8] to show how $R_0$ reached ~6 in Wuhan and ~7.8 in Shanghai before interventions were implemented [9]. A fifth study found that $R_0$ gradually increased from January 10 to January 24 with a peak of 3.82, and then fell below 1 on February 6 in Wuhan using a method to estimate the household reproduction number and calculate time-varying reproduction numbers in Wuhan city [10].

Another study used a stochastic transmission model [11] to estimate how transmission in Wuhan between December 2019, and February 2020 declined from 2.35, one week before travel restrictions were introduced on January 23 to 1.05 one week later [12]. The seventh and final study used a chain-binomial model [13] to estimate an $R_0$ of 6.94 for COVID-19 on the “Diamond Princess” cruise ship during the early intensive social contacts and that everyone on board would have been infected in one month if control and prevention measures had not been implemented [14].

In this study, we propose an improved algorithm for calculating R ₀ based on the SIR-based model developed for the COVID-19 outbreak in Hubei Province of China [5]:

$$R_0\left(t\right)=\frac{\beta \left(t\right)}{\gamma \left(t\right)+\mu \left(t\right)}=\frac{\text{d}I\left(t\right)/\text{d}t+\left(\gamma \left(t\right)+\mu \left(t\right)\right)·I\left(t\right)}{\left(\gamma \left(t\right)+\mu \left(t\right)\right)·I\left(t\right)·S\left(t\right)},$$ (1)

where $R_0\left(t\right)$ is the basic reproduction number at time $t$; $\beta \left(t\right)$ denotes the time-dependent transmission rate (TDTR); $S\left(t\right)$ represents susceptible fractions of the population at time $t$; $I\left(t\right)$ represents the infected fraction of the population at time t; $\gamma \left(t\right)$ is the recovery rate; and $\mu \left(t\right)$ refers to the fatality rate caused by COVID-19.

This improved algorithm utilizes the actual data without assuming a specific pattern and has less parameters than the original model. Our tests indicated that the improved $R_0\left(t\right)$ performs well on provincial and prefectural levels in China and on a national level across the world under any circumstances. The original model, in contrast, was not very stable when estimating the demise of the pandemic in several of the prefectures in Hubei Province.

The number of infected individuals of COVID-19 surpassed 28.21 million worldwide on September 11, 2020, according to the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University. The first 6 countries with the largest cumulative numbers of infected individuals were the United States of America, India, Brazil, Russia, Peru and Colombia in rank order. These countries were distributed across the Americas (4), Asia (1) and Europe (1).

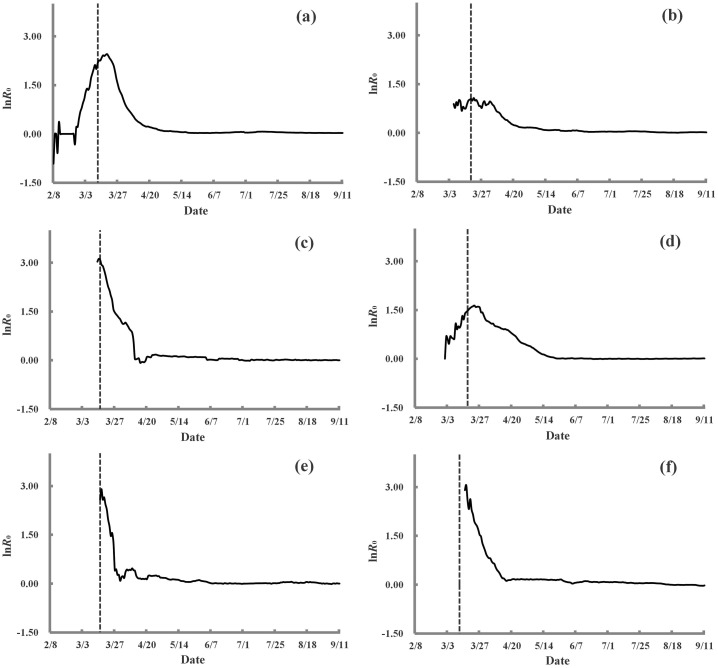
We here apply the improved algorithm for $R_0$ on the reported data about infected individuals, recovered individuals, and deaths caused by COVID-19 (Tables S1–S8 online) to monitor the transmission dynamics in the 6 countries. The natural logarithm of the basic reproduction number ($\mathrm{l}\mathrm{n}{R}_0$) is utilized to more clearly express the curves for the COVID-19 transmission dynamics across the six countries (Fig. 1 ).

Fig. 1.

Curves of the natural logarithm of the basic reproduction number ($\mathrm{l}\mathrm{n}{R}_0$) in the 6 countries with the largest cumulative numbers of infected individuals around the world: (a) United States of America, (b) India, (c) Brazil, (d) Russia, (e) Peru, and (f) Colombia. The dotted vertical line presents the date when the first intervention was launched.

The first case was reported on January, 22 in the United States of America. $R_0$ surpassed 2.0 on February 29, and then increased to the maximum value of 11.6 on March 19. In response to the rapid spread of COVID-19, the state of New York set up a “containment area” in a COVID-19 hotspot on March 12, with National Guard troops dispatched on site to clean surfaces and deliver food to people in quarantine. On March 16, at least four states and several large cities, including New York City and Los Angeles, ordered restaurants, bars and other businesses to close their doors. Many of the 50 states implemented stay-at-home orders to slow the spread of COVID-19 from March 18 onwards. $R_0$ has declined monotonically since March 20, falling below 2 on April 6 and to <1.1 on May 18. It oscillated between 1.0 and 1.1 from May 18 to July 29 and has since stayed at the critical value of 1 (Fig. 1a and Table S9 online).

The first case was reported on January 30 in India. $R_0$ increased with oscillations and reached its maximum value of 2.9 on March 21. Citizens were asked to isolate in their homes to protect themselves on March 19. In addition, they were urged to observe a self-imposed curfew on March 22 and a nationwide lockdown was imposed on March 25. $R_0$ declined at varying rates from March 21 onwards, falling below 2 on April 8 and reached 1.1 on May 9. It oscillated from 1.0 to 1.1 from May 9 to July 22 and achieved a value of 1.0. $R_0$ has persisted in its value of 1.0 since July 23 to the time of writing (i.e., September 11) (Fig. 1b and Table S9 online).

Brazil reported its first case on February 26 and recorded its peak $R_0$ of 22.6 on March 15. Several states had already taken measures to slow the transmission of COVID-19, such as suspending classes in schools and shutting theaters and concert halls prior to March 16. Public and private schools across these states were temporarily closed on March 23. Most Brazilian states imposed quarantines to limit people’s contact and asked stores not selling essential goods to close so as to contain the epidemic by the end of March. $R_0$ declined rapidly from March 16 onwards, falling below 2 on April 10 and below 1 for the first time on April 15. However, $R_0$ has oscillated between 1.0 and 1.2 from April 19 to June 23. $R_0$ has kept its value of 1.0 since June 24 (Fig. 1c and Table S9 online).

Russia reported its first two cases on January 31. On March 16, Russia restricted the entry of foreign citizens and stateless persons from March 18 to May 1 to help prevent the spread of COVID-19. According to available data, $R_0$ rose and fell in March. It reached its maximum value of 5.2 on March 23. Paid leave was granted to all Russians from March 30 to April 3 on March 25, and 32 of Russia’s 85 regions introduced mandatory self-isolation for all residents on March 30. Additional regions implemented the same measures soon thereafter. $R_0$ declined continuously from March 25 onwards, falling below 2 on April 24 and 1 on May 20. The latter value was sustained up to the time of writing (i.e., September 11) (Fig. 1d and Table S9 online).

In Peru, the first case was reported on March 6. $R_0$ reached its peak of 18.3 on March 17. Peru declared a state of emergency on March 16. The measures included a quarantine and a curfew as part of the efforts to stop the spread of COVID-19. $R_0$ started to decline on March 18 and fell below 2 on March 27. R ₀ has varied between 1.0 and 1.1 since May 6, but its value was still 1.0 at the time of writing on September 11 (Fig. 1e and Table S9 online).

In Colombia, the first case was reported on March 6. $R_0$ reached its peak of 21.2 on March 17. Colombia declared a nationwide health emergency, banning activities with >500 people on March 12 and later announcing a 30-d ban on all travelers coming from abroad, including nationals, from March 23 onwards. $R_0$ declined monotonically from March 21 to April 15, falling below 2 on April 6 and reaching 1.1 on April 16. An $R_0$ of 1.2 was sustained from April 18 to May 22, and it has oscillated between 1.0 and 1.1 since May 28 (Fig. 1f and Table S9 online).

In summary, the results produced with our new data-driven method for calculating $R_0$ indicate that interventions, such as lockdowns, quarantines, school closures, travel restrictions, and social distancing, have played a critical role in containing the spread of COVID-19. $R_0$ might have surpassed 41.5 if interventions had not been imposed in Turkey and this value of $R_0$ might have been attained in other locations as well if they had not intervened as promptly as they did (Table S9 online). The interventions have effectively changed $R_0$ from increasing to decreasing in all of the 6 countries that are distributed across the Americas, Asia and Europe that were highlighted in this paper.

Similar interventions were eventually implemented in all 6 countries. $R_0$ fell below 2 in all 6 countries on April 24, which means that major outbreaks are no longer likely. However, COVID-19 is continuing to spread in these countries because there is no country with $R_0$ < 1.0. Peru (2.23%), Brazil (2.06%), the United States of America (2.00%), and Colombia (1.43%) led in terms of the percentages of infected individuals as of September 11 (Tables S10 and S11 online).

The results clearly show that the interventions have produced large variations in effectiveness in different countries due to the various ways in which executive powers are exercised from one country to the next.

For instance, the interventions were very effective in Germany. Tough measures to limit social contacts were conducted uniformly in all 16 federal states of Germany in March and April 2020. It took just 26 d for $R_0$ to fall from its peak to <1 during the first outbreak in Germany (Table S9 online). However, COVID-19 started to rebound in Germany on May 11 because the pandemic interventions were relaxed. An $R_0$ of 1 has been continuously sustained in Germany for 130 d. The efficacy of the interventions is quite low in the United States of America. $R_0$ started to decline approximately one week after the interventions were implemented in the United States of America when most of the other countries highlighted in this paper saw rapid declines in $R_0$ in a few days following the initial interventions.

Conflict of interest

The authors declare that they have no conflict of interest.

Biographies

Tianxiang Yue is the head of Department for Eco-Environmental Informatics, Institute of Geographical Sciences and Natural Resources Research, Chinese Academy of Sciences. He received his Ph.D. degree in system ecology from Chinese Academy of Sciences in 1992. He has been working as a professor at State Key Laboratory of Resources and Environmental Information System since 2000. He is a pioneering expert in the method for high accuracy surface modelling and the fundamental theorem for eco-environmental surface modelling.

Bin Fan is a Ph.D. student of State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences. His major is Cartography and Geographical Information System and his research activities mainly focus on eco-environmental surface modelling.

Appendix A. Supplementary data

The following are the Supplementary data to this article: