Fig 1. Comparison of the sQSSA and tQSSA for an enzyme-catalyzed reaction.

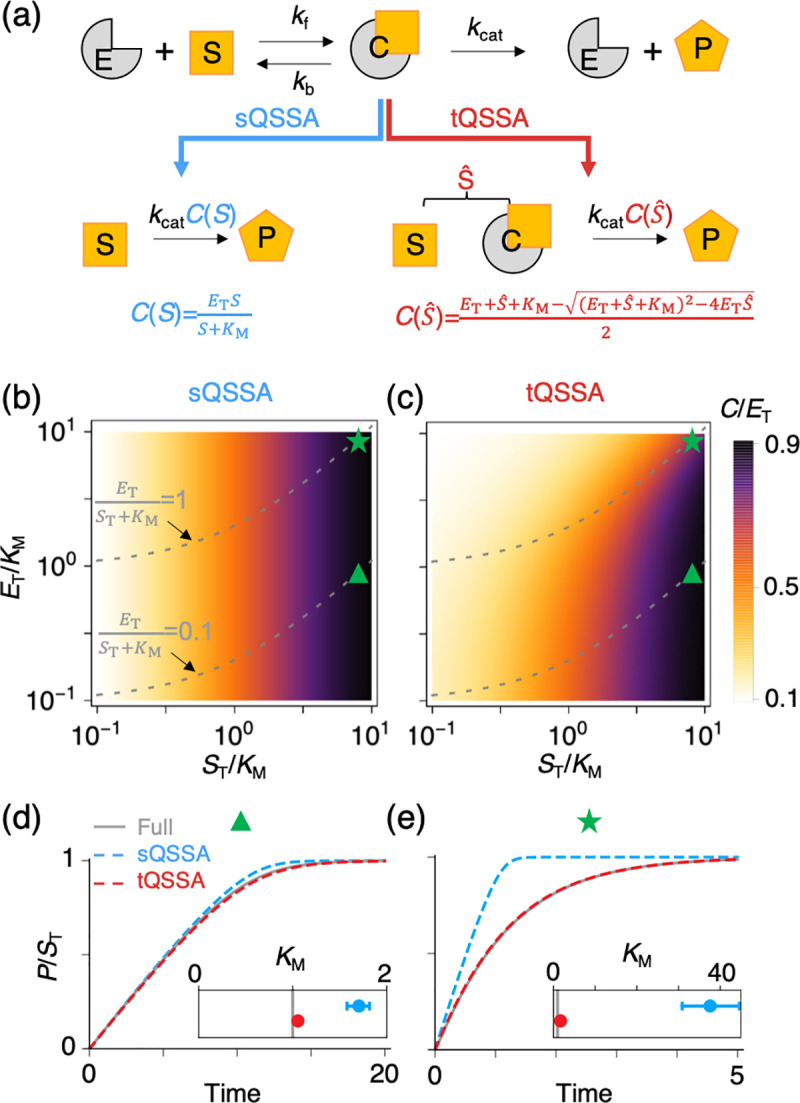
(a) The MM mechanism for a single-substrate enzyme-catalyzed reaction; S, substrate; E, enzyme; C, enzyme-substrate complex; P, product. Note that we use a different font style to distinguish a substance, S, from its concentration, S in Eq 1. The full model, based on mass-action kinetics (Eq 1), can be simplified by either the sQSSA (Eq 3) or the tQSSA (Eq 5). Both approximations assume that C rapidly reaches a QSSA, which is solely determined by either S (Eq 2) or $\widehat{S}=S+C$ (Eq 4). (b–c) Heat maps of the predicted maximal fraction of total enzyme that is in complex with substrate, i.e., C(S_T)/E_T, predicted with sQSSA (Eq 2) and tQSSA (Eq 4). In these panels, color represents the ratio C(S_T)/E_T, and gray dashed lines are contours of E_T /(K_M + S_T) = 0.1 and 1.0. The sQSSA (Eq 2) predicts that this fraction is independent of total enzyme concentration, E_T (e.g., C(S_T)/E_T = 0.5 when S_T = K_M regardless of E_T) in panel b. On the other hand, the tQSSA (Eq 4) predicts that, as E_T increases, more substrate is needed to achieve that same level of substrate saturation of enzyme molecules in panel c. When the validity condition for the sQSSA holds (i.e., below the gray dashed line where E_T /(K_M + S_T) ≪1), the predictions of the two models are nearly identical. (d–e) The simulated accumulation of P and the estimation of the Michaelis constant, K_M, from the progress curve of P. For these calculations, we chose k_f = 10, k_b = 9, k_cat = 1, K_M = 1, S_T = 9, and E_T /(K_M + S_T) = 0.1 (panel d; triangle mark in (b) and (c)) or 1 (panel e; star mark in (b) and (c)). Initial conditions are S(0) = S_T, C(0) = 0, P(0) = 0. If E_T is low (i.e., E_T /(K_M + S_T) = 0.1), the simulation of P and the estimation of K_M with the sQSSA model are accurate (d). On the other hand, if E_T is high (i.e., E_T /(K_M + S_T) = 1), the simulated P with the sQSSA model using the true rate constants is wildly divergent from the true progress curve simulated with the full model (e). As a result, if k_cat and K_M are adjusted to fit the sQSSA model to the true progress curve, then the estimates of k_cat and K_M are far from the true values (inset; the estimates of k_cat is not shown). On the other hand, the tQSSA model accurately reproduces the progress curve of P and estimates the rate constants regardless of the value of E_T (d and e). Inset: gray lines are the true value of K_M, and the red and blue circles are the mean K_M estimates from the tQSSA and sQSSA models, respectively. The bars represent 99% confidence intervals. The Quasi-Newton method is applied to 21 sampled points of the progress curve of P simulated with the full model to identify the value of K_M that minimizes the fitting error of the sQSSA and tQSSA models. The true values of parameters are used as the initial condition for the fitting procedure in order to avoid parameter unidentifiability. MM, Michaelis–Menten; sQSSA, standard quasi-steady state approximation; tQSSA, total quasi-steady state approximation.