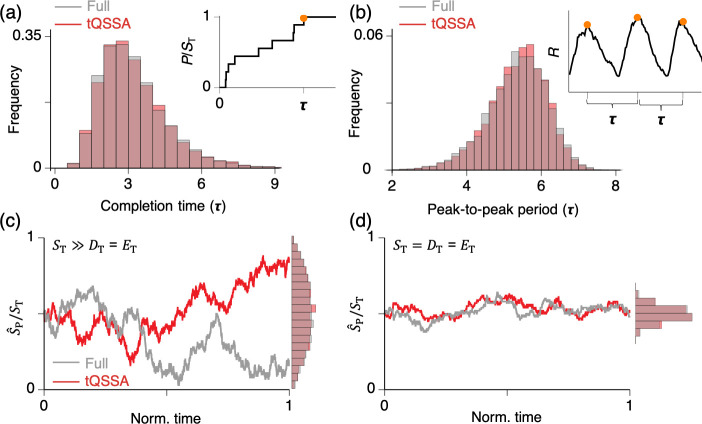
Fig 4. tQSSA provides accurate stochastic simulations.

(a) Catalysis-completion time τ (see inset) of the single-substrate enzyme-catalyzed reaction (Fig 1a) varies due to stochastic fluctuations. The distributions of τ simulated with the full model (3.24 ± 1.4) and the tQSSA model (3.22 ± 1.37) are nearly identical. Here, the same parameter set and initial condition are used as in Fig 1e and Ω = 1. Gillespie’s stochastic simulation algorithm is used [107]. (b) The peak-to-peak period τ (see inset) of simulated oscillatory trajectories for the model of a negative feedback loop (Fig 3b) fluctuates due to stochasticity. The distributions of τ simulated by the full model (5.3 ± 0.8) and tQSSA model (5.3 ± 0.78) are nearly identical. Here, the same parameter set and initial condition are used as in the inset of Fig 3d and 3e and Ω = 5 × 10⁻⁴. (c–d) In both the presence (c) and absence (d) of zero-order ultrasensitivity, stochastic simulations of the full and tQSSA models lead to nearly identical stationary distributions of ${\widehat{S}}_{\mathrm{P}}/S_{\mathrm{T}}$: 0.5 ± 0.23 and 0.5 ± 0.22 (c) and 0.5 ± 0.05 and 0.5 ± 0.05 (d). Here, E_T = D_T and the values of the other parameters are the same as used in Fig 2b and 2d for (c) and (d), respectively. Initial conditions are S_p(0) = S(0) = S_T/2, D(0) = E(0) = D_T, and Ω = 1. tQSSA, total quasi-steady state approximation.