Backbone Free Energy Estimator Applied to Viral Glycoproteins

Abstract

Earlier analysis of the Protein Data Bank derived the distribution of rotations from the plane of a protein hydrogen bond donor peptide group to the plane of its acceptor peptide group. The quasi Boltzmann formalism of Pohl–Finkelstein is employed to estimate free energies of protein elements with these hydrogen bonds, pinpointing residues with a high propensity for conformational change. This is applied to viral glycoproteins as well as capsids, where the 90th+ percentiles of free energies determine residues that correlate well with viral fusion peptides and other functional domains in known cases and thus provide a novel method for predicting these sites of importance as antiviral drug or vaccine targets in general. The method is implemented at https://bion-server.au.dk/hbonds/ from an uploaded Protein Data Bank file.

1. Introduction

The viral life cycle involves several activities: adsorption, entry, uncoating, transcription/mRNA production, synthesis of viral components, virion assembly, and release (Dimmock et al., 2017; Levine, 1992). Here, the first two stages are studied, which might be characterized as recognition/binding with the host cell (cf. Shanker et al., 2017; Boulant et al., 2015; Rossman, 1994) and subsequent fusion/penetration of cell or endosomal membrane (cf. Chernomordik and Kozlov, 2009; Harrison, 2008; Thorley et al., 2010; White et al., 2008; Tsai, 2007; Moyer and Nemerow, 2011). This is typically accompanied by a dramatic reconformation in order to fashion characteristic fusion/penetration motifs. A general method is presented here to predict such residues of high conformational activity from a 3D structure.

Viruses can be enveloped in a lipid bilayer, non-enveloped and contained in a protein capsid, or may be enveloped for only part of their life cycle. Enveloped viruses are understood best, and their envelopes support glycoproteins orchestrating both recognition/binding and fusion/penetration (see Choppin and Schied, 1980; Ward, 2015). With this case in mind, one might rightly think of the glycoprotein as a mechanical device primed for reconformation with appropriate stimuli.

The free energy of a protein feature provides a measure of its stability according to Finkelstein and Ptitsyn (2016). While most features of a protein must have low free energy in order to stabilize the structure, there are also energy defects as reflected by exotic features, as they shall be called here, with high free energy. Such exotic features occur rather rarely and may arise for functional reasons.

Such a defect may be tolerated, preserved by evolution and compensated by other low free energy regions, because it is required for protein function, especially in cases when the function consists of conformational change: an unstable feature will more likely change conformation in a biologically reasonable time, while a stable structure without defects would likely take too long to reorganize. Receptor-binding and fusion peptides are just such cases, as their function is connected with conformational change.

These considerations lead to the scrutiny of exotic features of viral glycoproteins undertaken here. This regime is probed by applying the quasi Boltzmann formalism, observed by Pohl (1971) and explained by Finkelstein et al. (1995a, 1995b), to the distribution of hydrogen bond geometry compiled in Penner et al. (2014) from an unbiased subset of the Protein Data Bank (PDB) described by Berman et al. (2000). Hydrogen bonds of a subject protein might be analyzed, and free energy differences of corresponding features computed via relative densities in the distribution with residues determined where conformational change is likely, which it has already been argued here should comprise significant functional domains.

In multiple cases where these regions have been determined, the method discussed here succeeds in accurately identifying them. This therefore offers the prospect of prediction in cases where they have not been determined.

After first reviewing background material, namely the application of the PDB-derived distribution using the quasi Boltzmann formalism, several viral glycoproteins are studied in detail to establish credibility of the method. The bulk of this article is a table for a multitude of viral glycoproteins containing those residues involved in features with high free energy hydrogen bonds between peptide groups as well as for several non-enveloped viral capsids.

These tables of residues offer prediction of recognition/binding, fusion/penetration, and other functional sites for viruses as argued above. This at least provides potential experimental targets for mutational knockdown of functional domains. These residues moreover provide appealing targets for drugs or vaccines not only because their obstruction should interrupt function, but also because exotic peptides by their very nature occur rarely in the host organism, therefore minimizing the likelihood of side effects. It is worth noting, however, that there are no human fusion peptides in the PDB at this time. So, this latter aspect is far from certain.

2. Background

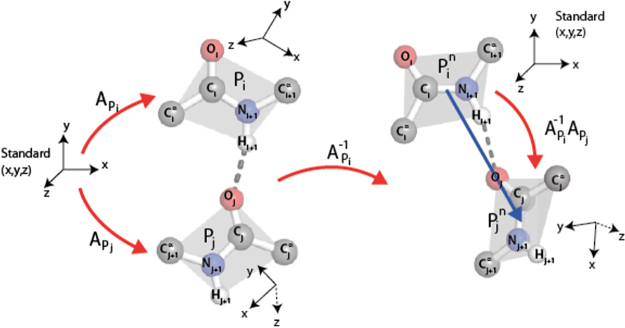
As introduced and developed by Penner et al. (2014) and illustrated in Figure 1, two peptide groups sharing a backbone hydrogen bond (BHB) ordered from donor to acceptor provide a unique rotation of 3D space as determined by an axis of rotation and an amount of rotation about it. The “collection of all 3D rotations” is abbreviated simply as SO(3), following mathematical traditions. Mathematics furthermore endows SO(3) itself with intrinsic notions of distance, angle, and volume (for further details, see Penner et al., 2014).

FIG. 1.

Two peptide groups, P_i, P_j, are depicted on the left, participating in a hydrogen bond with donor P_i and acceptor P_j. The planes of these peptide groups are illustrated in gray. There is a unique 3d rotation $A_{P_i}$ carrying the (oriented) xz plane to the gray plane for P_i and sending the positive x-axis to the ray $\overrightarrow{C_i{N}_{i+1}}$, and likewise $A_{P_j}$ for P_j. The composition $A_{P_i}^{-1}{A}_{P_j}$ illustrated on the right is the rotation in SO(3) associated to the pair P_i, P_j. See Section 5.2. for details.

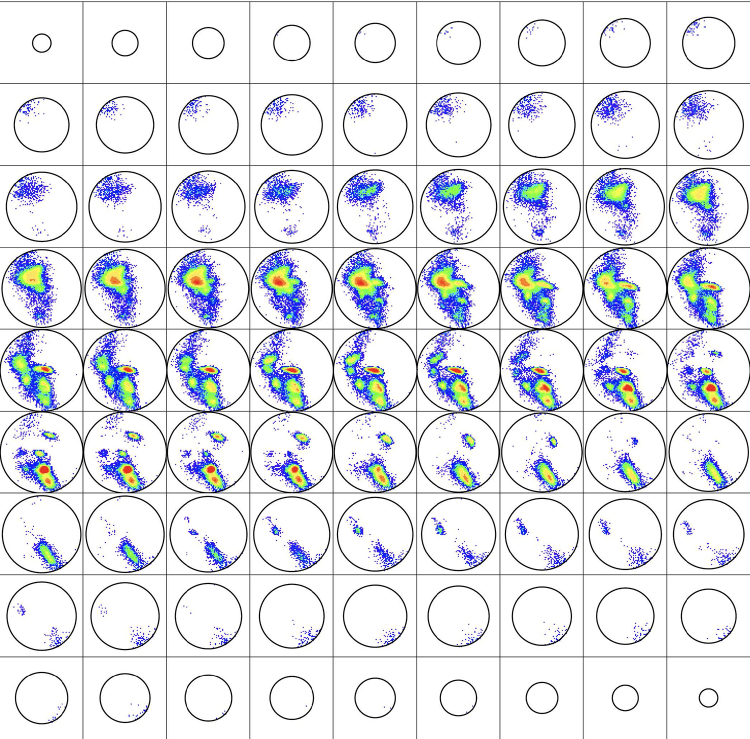
Upon choosing an unbiased representative subset of the PDB, called HQ60 for high-quality 3D structures with ≤60% homology identity, which is culled from the PDB using the software PISCES developed by Wang and Dunbrack (2003), one might study the histogram of all BHBs that occur, some 1,166,165 in number (see Section 5.2. for more detail). The results reveal that the rotations that occur for these BHBs (or, as abbreviated, simply the BHBs themselves) in HQ60 occupy only about 32.5% of the volume of SO(3). This distribution in SO(3) is depicted in Figure 2.

FIG. 2.

As explained in Section 5.2., SO(3) may be visualized as a 3D ball of radius π. Presented here are 81 horizontal slices of the histogram of backbone hydrogen bond (BHBs) in HQ60 in this ball from north to south pole colored by population density from Penner et al. (2014), where the R-Y-G-B color is linear in the density ranging from 19,000 to 1.

As explained in Finkelstein and Ptitsyn (2016, lecture 16), specific features of proteins obey a so-called quasi Boltzmann law in the sense that feature occurrence is proportional to $exp\left(-F∕k{T}_C\right)$, where F is the free energy of the feature, k is the Boltzmann constant, and T_C is an effective temperature, the conformational temperature of approximately 350 K, roughly the melting temperature of protein, with $k{T}_C$ about 0.7 kcal/mole at room temperature, compared to $kT=0.6$ kcal/mole, with T the temperature about 300 K. These are not Boltzmann statistics in the usual sense of a particle visiting states with a probability proportional to the energy divided by $-kT$, but rather reflect the statistics of words in the alphabet of amino acids that stabilize proteins with the particular feature (cf. Finkelstein and Ptitsyn, 2016; Finkelstein et al., 1995a, 1995b).

More explicitly, consider again the distribution on the 3D ball SO(3) illustrated in Figure 2. SO(3) is dissected into roughly a quarter million boxes of small equal Euclidean volume, and the density $d\left(p\right)$ at any BHB rotation p in SO(3) is the number of points of the distribution in the box containing p divided by the SO(3) volume of the box. Thus, the density is determined as a function of SO(3) that takes a constant value on each box. There is a point m in SO(3) of highest density $d\left(m\right)=19000$ at the rotation unsurprisingly corresponding to the ideal (right-handed) α helix. To fix an overall scale, the quantity

$$\Pi \left(p\right)=ln\left[d\left(m\right)∕d\left(p\right)\right]$$

is taken as a descriptor of the point p in SO(3). By the quasi Boltzmann Ansatz, differences $\Pi \left(p_1\right)-\Pi \left(p_2\right)$ agree with free energy differences in $k{T}_C$ units between protein features corresponding to p₁, p₂.

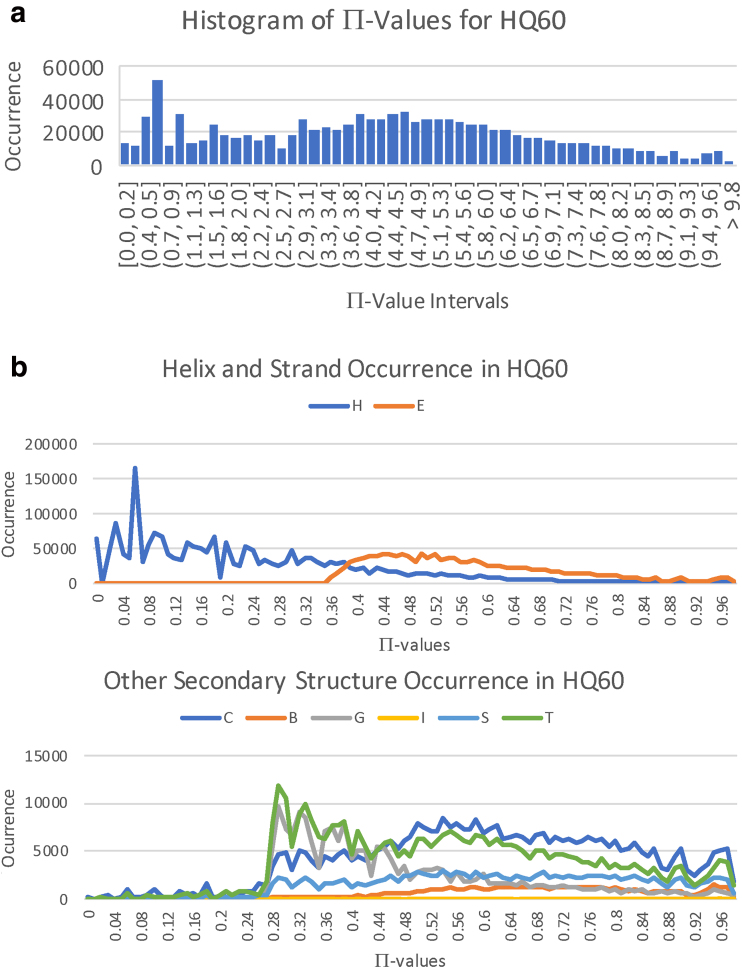
The histogram of $\Pi \left(p\right)$ over HQ60 in $k{T}_C$ units (henceforth, the units $k{T}_C$ in $\Pi$-values are usually suppressed) is given in Figure 3a. Taking a normalizing shift to the left of −2 kcal/mole ≈ −2.9 kT_C for the nominal free energy of an α helix as in Finkelstein and Ptitsyn (2016) to be that of the ideal α helix, which has $\Pi =ln1=0$, the free energy for the protein feature stabilized by p is given by $\left[\Pi \left(p\right)-2.9\right]k{T}_C$. This scheme assigns absolute free energies to protein features and justifies computing these quantities separately for subunits of an entire protein, even though $T_C\approx$ melting temperature depends upon the protein. It also gives an internal consistency check that this shift gives a maximum free energy just below the bounds of protein stability. The $\Pi$-values themselves will be employed in the sequel. A BHB with $p\in SO\left(3\right)$ is exotic if $\Pi \left(p\right)\ge 7.5$, and a residue $N_i-C_i^{\alpha }-C_i$ is exotic if either $N_i$ or $C_i$ participates in an exotic BHB. In fact, $\Pi \left(p\right)\ge 7.5,8.5,9.5$, and 9.85 essentially correspond to the respective 90th, 95th, 99th, and 100th percentiles of Π-values across HQ60.

FIG. 3.

Histogram of Π-values and of flanking Dictionary of Secondary Structure for Proteins (DSSP) secondary structure types across HQ60. (a) Histogram of Π(p) = ln(d(m)/d(p)) for all BHBs across HQ60. The x-axis corresponds to the indicated intervals of II-values achieved for the BHBs in HQ60, and the y-axis indicates the number of occurrences in HQ60 within each interval of size 0.18. (b) Population of flanking DSSP secondary structure types H (α helix), E (β strand), C (coil), B (β bridge), G (3₁₀ helix), 1 (π helix), S (bend), and T (turn) across the range of Π-values divided by 10 along the x-axis.

The distribution of flanking Dictionary of Secondary Structure for Proteins (DSSP) secondary structure types from Kabsch and Sander (1983) for HQ60 across the free energy spectrum is shown in Figure 3b aligned to Figure 3a, where the residues $i,i+1,j-1,j$ are said to flank the BHB $N_i-H_i::O_j=C_j$. Note the predominance of α helixes for small free energy, and the mixture of all secondary structure types for large free energy.

3. Results

Representative concrete examples of fusion glycoproteins treated in White et al. (2008) are first analyzed in detail here, namely for the influenza, paramyxovirus, tick-borne encephalitis, and vesicular stomatitis viruses. Influenza is taken as a case in point in order to explain in greater detail these several analyses.

3.1. Narrative discussion of test cases

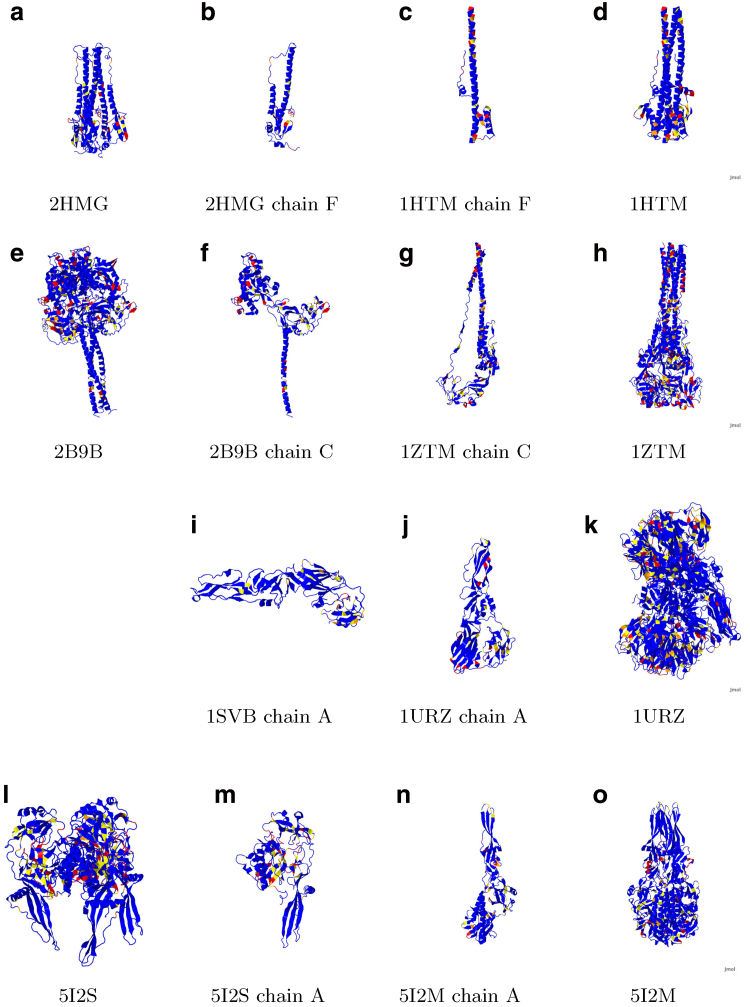
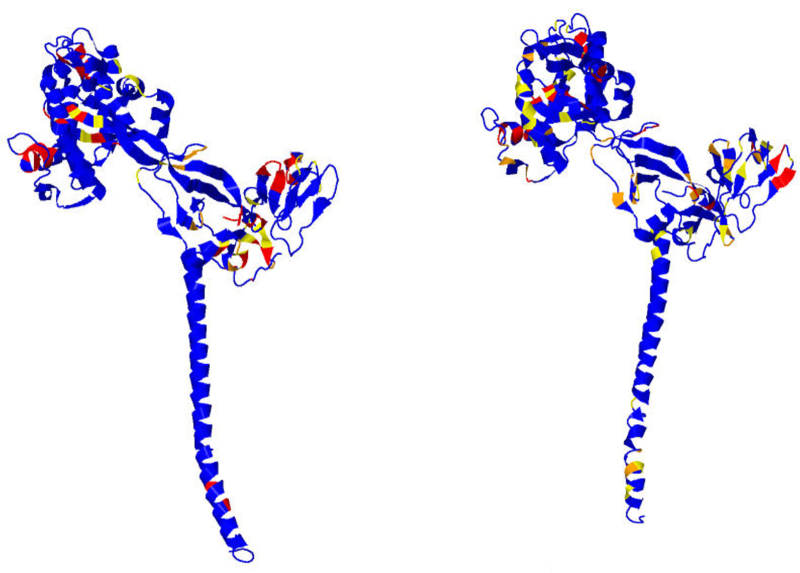
Figure 4 depicts the various glycoproteins aligned to figure 6 of White et al. (2008) to which it should be compared. The color scheme here is that blue indicates non-exotic, yellow above the 7.5 cutoff, orange above the 8.5 cutoff, and red above the 9.5 cutoff for Π-values, which respectively correspond to the 90th, 95th, and 99th percentiles. As a notational convenience for this discussion, if the residue N is involved in an exotic BHB, then one writes Nb, Ny, No, Nr to indicate this discretization of Π-values into colors, also letting Nx indicate that N is involved in an exotic BHB with the 100th percentile Π-value of 9.85.

FIG. 4.

Compare with Figure 6 in White et al. (2008), to which these images are aligned. Blue indicates non-exotic, and yellow, orange, and red, respectively, correspond to Π-values at least 7.5, 8.5, and 9.5. Influenza hemagglutinin (HA; a,b) prefusion and (c,d) postfusion. Paramyxovirus glycoprotein F (e,f) prefusion and (g,h) postfusion. Tick-borne encephalitis glycoprotein E (i) prefusion and (j,k) postfusion. Vesicular stomatitis glycoprotein G (l,m) prefusion and (n,o) postfusion.

FIG. 6.

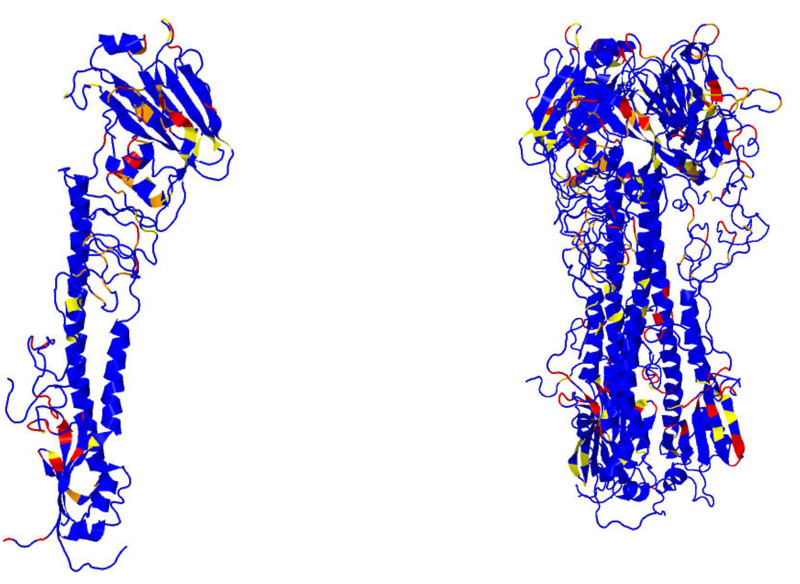
Paramyxovirus F prefusion, chain A on the left and chain B on the right. There is only approximate consensus on significant free energies between chains A and B and chain C in Figure 4f.

Required for complete investigation here of influenza hemagglutinin (HA) are both pre- and postfusion 3D structures, as respectively provided for the fixed strain H3N2 of influenza HA by the PDB files 2HMG and 1HTM. However, either conformation alone could provide relevant data for drug or vaccine design. Concentrating now on just one monomer of the trimer HA, the exotic BHBs for chains E and F prefusion and chain F postfusion are computed by the methods here and enumerated in Table 1 in order of non-decreasing Π-values; for chain F, the exotic residues lying in the fusion peptide are highlighted in boldface prefusion but are absent postfusion, since the fusion peptide itself is missing from the PDB file. These results are depicted in Figures 4a–d and 5. The functions of various peptides in chains E and F are next discussed.

Table 1.

Exotic BHB Donor/Acceptor Residues Viral Glycoproteins for Test Cases

Influenza Virus Type A Glycoprotein HA Prefusion (2HMG)

Chain E

90–94% 116/111 241/170 258/121 16/F136 256/150 86/57 158/160 221/227

95–98% 284/286 288/50 150/72 253/181 65/61 308/293 114/109 304/F62 135/153 157/194 137/146 142/144

99% F15/17 161/157 F24/16 74/68

100% 19/F21 20/F14 29/31 95/63 106/102 124/255 147/136 198/195 207/209 254/152 F63/303

Chain F

90–94% E16/136 36/24 101/96 9/5

95–98% 130/126

99%15/E17 24/E16

100%E19/21 E20/14 10/4 11/5 63/E303 134/137 175/172

†Influenza Virus Type A Glycoprotein HA Postfusion (1HTM)

Chain F

90–94% 128/123 61/56 92/87

95–98% 63/59 107/103 134/137 50/45

99% 132/139

100% 44/40 57/52 108/102 160/157

Paramyxovirus Glycoprotein F Prefusion (2B9B)

Chain A

90–94% 259/272 170/166 241/237 408/424 269/263 334/39 295/301 294/367 98/95 423/411 362/300 352/348

95–98% 38/329 313/315 422/B106 354/351 328/330 297/299

99% 258/219 373/375 300/296 262/270 491/486 24/21 441/437

100% 26/22 92/87 94/91 95/90 96/90 160/156 188/184 189/184 264/268 353/347 374/B114 376/372 416/418 419/415

Chain B

90–94%132/127 167/150 68/65 483/478 300/296 296/401 357/353 269/263135/130 449/445 258/219 129/124 496/491 390/412 181/60 70/66 313/315 408/424 377/405

95–98% 334/39 31/25 374/C114 113/109 376/372387/414 82/77 492/487 A422/106 145/141 315/312 297/299 319/339

99% 388/392 93/88 90/85 262/270 188/184

100% 27/23 46/275 92/87 95/90235/231 236/231 264/268 328/330 393/387 416/418 A374/114

Chain C

90–94% 484/479 271/261 29/25 384/379 416/418 220/257 377/405 373/37526/23 38/329 313/315 170/166 411/407 300/296 258/219 296/401 319/339 353/347

95–98% 297/299 387/414 95/89 157/159 31/25 269/263 94/91

99% 269/263 94/91 328/330 473/469

100% 96/90 102/96 113/109 188/184 189/184 264/268 278/43 388/392 393/387 408/424 485/480

†Paramyxovirus Glycoprotein F Postfusion (1ZTM)

Chain A

90–94% C59/443 323/319 29/25 261/257 210/205 264/281 326/346 408/404 158/153 262/256 361/358 366/363 271/275 C53/438 193/189 215/210 244/240 243/239

95–98% B229/219 254/249 84/79 423/425 395/399 289/38 363/359 229/C219 303/408

99% 360/354 167/162 185/179 307/303448/445 353/349 469/464 460/456 63/59

100% 30/26 31/25 38/336 155/150 166/161 199/194 216/211 235/231 242/238 320/322 354/349 380/382 421/427 470/465

Chain B

90–94% 53/C438 88/83 191/186 426/422 174/169 276/270 303/408 264/28195/90 462/457 C229/219 395/399 184/178271/275 234/230

95–98% 229/A219 215/210 233/228 380/382 320/322 187/182 87/83 421/427

99% 423/425 335/337 38/336 366/363 172/167 262/256361/358

100% 31/25 83/7984/79 84/80 185/179 196/192 197/192 244/240 305/405 327/315 383/379 484/479

Chain C

90–94% B53/438 59/A44329/25 301/374 155/150 42/340 235/231 31/25 83/79 463/458 233/228 271/275 151/146 229/B219 53/A438 476/472 283/45 383/380 408/404326/346

95–98% 328/344 30/26 26/22 203/198 387/375 185/179 184/178

99% 380/382 474/469 149/144 472/467

100% 38/336 95/90 148/143 244/240 264/281 303/408 320/322 332/328 360/354 361/358 363/359 394/421 421/427 470/465

Tick-Borne Encephalitis Virus Glycoprotein E Prefusion (1SVB)

Chain A

90–94% 218/196 188/289 386/388 330/316 389/385 65/120 177/180 308/339 322/325 339/364 355/344

95–98% 167/169 278/280 184/293380/394 372/148 388/309

99% 366/368 360/373

Tick-Borne Encephalitis Virus Glycoprotein E Postfusion (1URZ)

Chain A

90–94% 258/241 28/286 29/45 380/394 218/196 278/280 181/177 388/309 317/329 355/344 78/74 106/100 360/373

95–98% 249/251 389/385147/40 330/316

99% 322/325 180/176 243/238 366/368 371/363 15/18 9/302

100% 16/B13 167/169 177/180 192/285 251/248 252/248 C16/13

Vesicular Stomatitis Virus Glycoprotein G Prefusion (5I2S)

Chain A

90–94% 224/226 313/262 332/6 320/322 185/43 314/328 37/33 324/403 9/329 55/134 183/45 136/144 372/316 150/159 16/325 345/342 298/400

95–98% 104/98 333/208 38/190 51/47

99% 323/319 254/220 370/373 355/345 367/363 142/137 33/29 312/330 208/210

100% 138/142 146/151152/148 261/234 348/352 351/347 359/10 364/366 404/321

Vesicular Stomatitis Virus Glycoprotein G Postfusion (5I2M)

Chain A

90–94%72/75 332/6 119/115 254/220 225/138 377/379 258/254 261/234 216/203 219/215 38/190

95–98% 312/330 374/370 71/118 34/29 153/149 404/261

99% 348/352 15/12 138/142 146/151 152/148 208/210

100% 105/98 364/366 370/373

Donor/acceptor residues of BHBs in order of non-decreasing Π-values, with 7.5, 8.5, 9.5, and 9.85, respectively, corresponding to percentiles 90, 95, 99, and 100. The residues lying in generally agreed upon fusion loops are shown in bold.

^†Fusion loop is missing from the structure and therefore a fortiori contains no exotic BHBs.

FIG. 5.

Influenza type 2 HA pre- and postfusion, both HA1 and HA2. Chains E and F are depicted on the left, and full glycoprotein on the right.

3.1.1. Influenza (PDB files 2HMG and 1HTM)

As per White et al. (2008), for chain F prefusion: residues 4x,5x form the fusion peptide with 9y,10x,11x and 14x,15r the nearby loop; 62o,63x account for helix extension; 96y,101y account for C-terminus inversion; 172x,175x form the C-terminus linker; 21x,24r,36y account for movement of the fusion peptide; and 126o,130o,134x,136x,137x are of function unmentioned in White et al. (2008) prefusion and reorganize postfusion to form the C-helix. For chain E prefusion, the residues 135o,136x,137o and 221y,227y pinpoint the sialic acid binding sites with the others of unknown function.

Thus, all of the exotic residues in chain F prefusion are explained by function, and only these arise from the method. For the other three viruses, the analogous narrative comparisons given next are also substantive, and again essentially all of the prefusion exotic residues in Table 1 accord perfectly with expectations, as next detailed.

3.1.2. Paramyxovirus (PDB files 2B9B and 1ZTM)

Paramyxovirus is shown in Figures 4e–h and 6. There is only approximate consensus among the three chains A, B, and C. For the prefusion chain A, B, and C consensus exotic residues as per White et al. (2008) and using the color scheme of chain C depicted in Figure 3: 90x,91x,92,93,94r,95o,96x lie in the fusion peptide; 264x,269r lie at the C-terminus of the helix extension domain; 297o,299o lie adjacent to the C-terminal inversion domain; 484y lies in the C-helix; 330r lies in a loop in domain II; and 414o,416y lie in a loop in domain I. Concentrating just on chain C and considering only colors R and X: 43x lies at the beginning of a β strand in DIII prefusion and in the middle of a β sheet postfusion; 90x,91r,94r,96x,102x,109x,113x lie in the fusion peptide, 184x,188x,189x lie in the C-terminus extension domain; 263r,264r,268x,269x lie in a loop and β turn region prefusion and comprise a β sheet postfusion; 278x lies in a loop between DI and DII prefusion and comprise a β sheet postfusion; 328r,330r lie in a β turn region prefusion and in a short β sheet postfusion; 387x,388x,392x,393x,408x,424x lie in a short β sheet prefusion and comprise a loop postfusion; and 469r,473r,480x,485x lie in the C-terminus inversion domain. All R and X bonds of chain C prefusion exhibit postfusion DSSP secondary structure reconformation consistent with expectations.

3.1.3. Tick-borne encephalitis (PDB files 1SVB and 1URZ)

Tick-borne encephalitis is shown in Figure 4i–k. Concentrating here primarily on O and R prefusion as per White et al. (2008): 307y,309o lie in the inversion loop; the fusion peptide is not exotic prefusion, although residues 74,78,100,101,105,106 all have Π-values >7.0, which is significant but below the cutoff, but with colors 74y,78y,100x,106x postfusion; the ij loop is unremarkable prefusion, but postfusion contains 248x,249x,251x,252x; 148o prefusion lies in a loop in DI that is not exotic postfusion; in contrast, 167o,169o prefusion also lie in a loop in DI, which however becomes red postfusion; 184o lies in the middle of a β strand both pre- and postfusion; 278o,280o lie in a loop prefusion and in a β turn postfusion; 360r,366r,368r lie in a loop in DII prefusion that remains red postfusion; 372o,373r lie in the middle of a β strand in DI both pre- and postfusion but colored 372b,373y postfusion; and 388o,394o lie at the beginning and end, respectively, of a β strand prefusion and likewise postfusion but with an orange residue now between them. It appears that the fusion peptide is not composed of exotic residues until after the pre- to postfusion transition and that the ij loop is unremarkable pre- and exotic postfusion. Moreover, all of 148o,372o,373r appear to lose free energy in the pre- to postfusion transition. In contrast 167o,169o and 360r,366r,368r become or remain red postfusion, suggesting either possible false-positives or some further activity involving them to follow the postfusion conformation. Meanwhile, 278o,280o undergo transition from loop to β turn consistent with losing free energy for reconformation; in contrast 388o,394o retain their β strand conformation but decrease free energy and produce an orange residue between them postfusion.

3.1.4. Vesicular stomatitis (PDB files 5I2S and 5I2M)

Vesicular stomatitis is shown in Figure 4l–o. As per White et al. (2008) prefusion: extension domain 1 has no BHBs at all except for the nearby exotic 183y,185y, while extension domain II contains the exotic 29r,33r,38o; the fusion peptide is not exotic prefusion and contains 115y,118o,119y and 71o,72y,75y postfusion. Considering only O, R, and X, there are two general rules from pre- to postfusion transition: DSSP secondary structure conformation is preserved, and the free energy is non-increasing. The notable exceptions are: the loop 261x changes conformation to the end of a short β 261o; the loop 404x at the C-terminus becomes the short β 404o; the end of the β strand plus loop 370r,373r becomes the more exotic 370x,373x; and the loop 10x becomes 12r,15r. Except for these few cases and the fusion peptide, the free energy of exotic peptides is again diminished or preserved from pre- to postfusion, and all residues that are exotic postfusion are already exotic in the prefusion conformation. This finding is consistent with the fact that this glycoprotein, unique among those considered in this section, is capable of oscillating between its pre- and postfuson conformations.

3.2. Quantitative discussion of test cases

In order to provide a quantitative measure of the predictive power of the methods here, a residue of a viral glycoprotein is defined as active if one of its standard conformational angles $\varphi$ or $\psi$ changes by at least 180° from pre- to postfusion conformation. The basic quantifiable assertion is: A prefusion exotic residue is at most one residue away along the backbone from an active one. The converse implication does not hold, however.

To test this hypothesis, the residues common to the pre- and postfusion conformations must be aligned, and this is accomplished in Supplementary Table S1 for HA chain F. One finds R = 122 residues common to the two conformations and that there are b = 33 active residues, and c = 19 inactive residues that are next to an active one with a = 70 that are not. A trial producing $n_b,n_c,n_a$ of these respective types has the natural trinomial probability given by $\left(\begin{array}{c}{n}_a+n_b+n_c\\ n_a{n}_b{n}_c\\ \end{array}\right){\left(\frac{70}{122}\right)}^{n_a}{\left(\frac{33}{122}\right)}^{n_b}{\left(\frac{19}{122}\right)}^{n_c}$, and the triples $\left(n_a,n_b,n_c\right)$ admit the natural lexicographic order derived from ≤ on the first and ≥ on the remaining two entries (see Section 5.3. for further details).

The seven exotic prefusion residues displayed in Supplementary Table S1 are numbered 62, 96, 101, 130, and 134–136, with $n_a=n_b=3$ and $n_c=1$, and one computes a p-value of $6.2\times 10^{-3}$. The other three examples likewise give statistically quite meaningful results based upon 168 further exotic residues among 1329 total residues common to pre- and postfusion conformations for the four glycoproteins, as presented in Table 2. Table 3 likewise presents p-values for the other examples discussed in detail in White et al. (2008) based upon their exotic BHBs presented in Table 1.

Table 2.

Conformationally Active and Exotic Residues in Test Cases

Viral glycoprotein	#Residues	Further than one away from active	Active	One away from active	#Exotic
Influenza glycoprotein HA chain F	122	70	33	19	7
Paramyxovirus glycoprotein F chain A	422	81	251	90	62
Tick-borne encephalitis glycoprotein E chain A	376	120	148	108	34
Vesicular stomatitis glycoprotein G chain A	409	140	138	131	72

Displayed are the data upon which the p-values in Table 3 are based. For each virus, the pre- and postfusion PDB files are aligned in order to compare the change of conformational angles during reconformation.

^#Residues is the number of residues common to the aligned pre- and postfusion conformation PDB files, and ^#Exotic is the number of exotic prefusion residues, namely the number of predictions to be made.

Table 3.

Distance d to Nearest Active Residue for Exotic Residues

Viral glycoprotein	d = 0	d = 1	d = 2	d > 2	First p-value	Second p-value
Influenza glycoprotein HA2 chain F	2/1	2/1	0/0	0/1	$6.2\times 10^{-3}$	$2.8\times 10^{-2}$
Paramyxovirus glycoprotein F chain A	27/15	6/8	1/1	3/1	$2.3\times 10^{-2}$	$7.2\times 10^{-2}$
Tick-borne encephalitis glycoprotein E chain A	7/7	2/9	0/5	2/2	$2.3\times 10^{-4}$	$1.2\times 10^{-1}$
Vesicular stomatitis glycoprotein G chain A	17/4	12/15	2/10	3/9	$4.8\times 10^{-1}$	$4.8\times 10^{-3}$

Results presented as dissipative/conservative, where these notions are defined in Section 5.3. p-Values computed for the trinomial distribution discussed before. The first p-value tests significance of the implication: if a residue is exotic prefusion, then it is at most one residue away from an active residue, and for the second p-value, all conservative results are discarded. Vesicular stomatitis is exceptional because its glycoprotein G can oscillate between pre- and postfusion conformations evidently with conserved exotic residues. See Section 5.3. for further detail.

3.3. Further results

Supplementary Table S2 provides the exotic residues for a host of viral glycoproteins analogous to Table 1. Another validation of the method here is that there is evidently fine agreement between Supplementary Table S2 and the known fusion loops with a few exceptions as noted. Moreover, in all cases scrutinized for receptor-binding domain, the tables compare favorably with the literature.

Supplementary Table S3 displays exotic residues for a selection of non-enveloped viral capsids, about whose recognition/binding and penetration mechanisms much less is known (cf. Tsai, 2007; Moyer and Nemerow, 2011). For the best studied polio virus, the exotic regions of VP1 adjacent to VP4 interior to the capsid are consistent with what is in the literature (cf. Tuthill et al., 2006; Rossman, 1994), where VP1 and VP4 are implicated in penetration, although VP4 itself contains only one exotic residue. Moreover, appropriate residues in the canyon walls presumed to be associated with receptor binding as in He et al. (2000) and Rossman (1994) are found to be exotic for both polio and rhinovirus. By analogy, for the other entries in Supplementary Table S3, under the assumption that penetration peptides must be shielded from the immune system, the exotic residues interior to the capsids provide natural predictions for penetration peptides, as do the exotic exterior residues for receptor-binding domains.

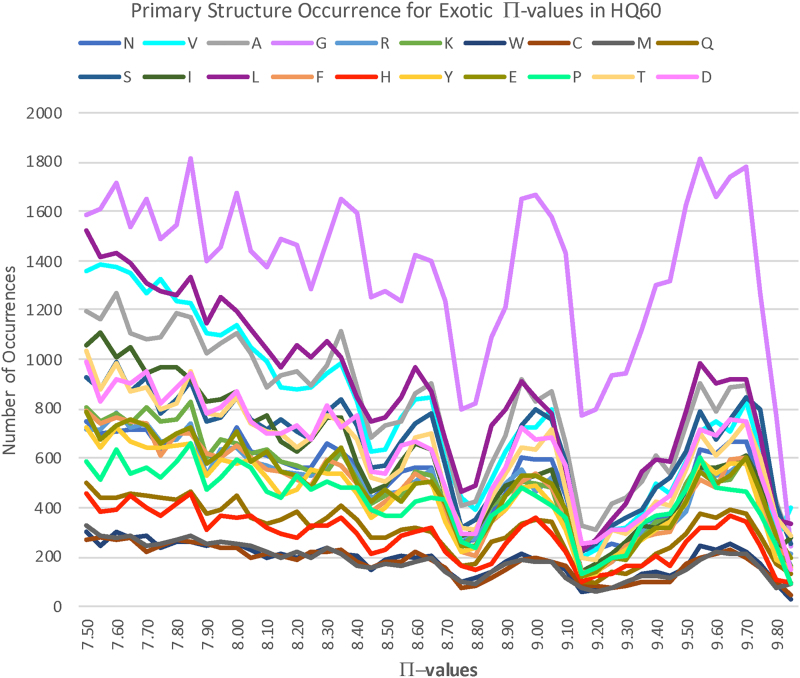
A striking phenomenon is evident in Figure 7: there are intervals of exotic free energy within which specific families of flanking amino acids vary together, one with another. This strongly suggests that there are characteristic primary structure motifs contributing to high free energy. These motifs should be retrievable with machine learning. More generally, this approach should open the possibility for backbone free energy estimation based upon primary structure alone, that is, a PDB file would no longer be necessary.

FIG. 7.

Histogram of Π-values and flanking primary structure for all exotic BHBs across HQ60. Curves are colored by residue as indicated. Note the increasing frequency of glycine reflecting the presumably progressively contorted exotic features that the primary structure must support.

4. Discussion

The overall point is that given the 3D prefusion structure of a viral glycoprotein, these methods furnish an ordered list of pairs of residues involved in exotic BHBs, and the latter entries among this list, those of highest free energy, provide most promising targets for antiviral drugs or vaccines. More refined predictions can be made by comparing exotic residues of viral glycoproteins pre- and postfusion, in complex with antibodies or in complex with receptors. Furthermore, there is the prospect with machine learning of making said predictions on the basis of primary structure alone.

There is the general pattern that fusion peptides and receptor-binding domains are exotic, the latter typically less so than the former, and the fusion loop hidden prefusion as for influenza and flaviviruses or only partially composed and exposed as for vesicular stomatitis or hidden as for tick-borne encephalitis, with similar remarks often for receptor-binding domains. Based on this scant circumstantial evidence, one might ask whether the host immune system can detect exotic protein features.

It is worth emphasizing that this idea of estimating free energies using exotic protein features in order to locate conformationally active sites must surely be more widely applicable in protein science and structural biology, for example in tyrosine kinase receptors, for which there are promising preliminary results. Other seemingly natural candidates for the method include certain prion, transmembrane, signal transduction, and cell motility proteins.

5. Methods Details

5.1. Bioinformatics methods

A DSSP prospective BHB $N-H::O=C$ is accepted provided that furthermore $|H-O|<2.7$Å, $|N-O|<3.5$Å and $\angle NHO,\angle COH>90^{\circ }$.

Using lower quality 3D structures and both higher and lower homology identity establish robustness of the basic properties of the distribution of BHBs from HQ60 in SO(3) over the data employed to compute it. Moreover, one must confirm that these constraints are not simply steric in nature, and indeed in excess of 95% of SO(3) is achievable by pairs of peptide groups at the distance scale of hydrogen bonds. A Density Functional Theory solution of the Schrödinger equations for pairs of peptide groups in Penner et al. (2014) essentially reproduces the empirically discovered region, thereby showing that the constraints are partly quantum physical. In fact, within this subspace containing all BHBs in HQ60, there is evident grouping into 30 distinct regions, various attributes of which are given Penner et al. (2014; Table 1). However, this clustering is entirely immaterial to the considerations of the current article. Indeed, a recent further analysis within clusters (which is not presented here) reveals that they are highly anisotropic and fail to remotely resemble a normal distribution therein, thus the attention here only on the PDB-derived distribution depicted in Figure 2. Given two peptide groups, there is not only the rotation between them, but also the displacement between their N-terminal alpha carbons, and one might wonder about including these translations as a further aspect of peptide group comparison. It was already determined in Penner et al. (2014) that this adds nothing, since the translation is essentially determined by the rotation.

The server https://bion-server.au.dk/hbonds/ for a given PDB file returns a list of its BHBs together with the density $d\left(p\right)$ relative to HQ60 of each BHB, as discussed in the main text. The BHBs are then rank ordered by Π-values, and only those exceeding the percentile cutoffs are considered.

Extensive tables of viral glycoproteins are presented in Supplementary Tables S2 and S3. Indicated in boldface are the residues lying in generally agreed upon fusion loops, which are taken ±2 residues to reflect uncertainty in precise peptide boundaries. Several table entries in Supplementary Table S2 are not fusion peptides but are included to show receptor-binding domains, for instance.

A few words are in order about the method in general and these tables in particular. Comparison with the residue B-values reported in the PDB files should be taken into account with large B-values (which measure the disorder of the protein; cf. Carugo, 2018) at a residue presumably casting potential doubt upon the verity of the reported high free energy. At the same time, the exotic residues determined here for PDB files with large reported resolutions might likewise be questioned, though an extensive study of influenza virus type A HA (not reported here) found the resulting exotic residues basically insensitive to reasonable resolutions, say, <3.5–4.5 Å.

5.2. Geometric methods

Several data are not indicated in Figure 1: the distance $|i-j|$ of residues along the backbone, the length $|O_j-H_{i+1}|$ of the BHB and the backbone conformational angles ${\psi }_i$ and ${\varphi }_{i+1}$, namely the respective rotation angles about the $C_i^{\alpha }$-C${}_i$ and N${}_{i+1}$–$C_{i+1}^{\alpha }$ axes.

Here is another explanation of the descriptor in SO(3) associated to a BHB in Figure 1. The cross-product (in this order) of displacement vectors $\overrightarrow{C_i^{\alpha }{C}_i}$ and $\overrightarrow{C_i{O}_i}$ determines a unit vector perpendicular to the plane of peptide group $P_i$, and this plane contains the unit vector parallel to the displacement vector $\overrightarrow{C_i{N}_{i+1}}$ of the peptide bond. The cross product of these (in this order) determines a third vector. There is a unique 3D rotation $A_{P_i}$ mapping unit vectors parallel to the z-, x-, and y-axes, respectively, to these three vectors (in these orders), and likewise $A_{P_j}$ for the peptide group P_j. In order to obtain a result that is independent of the position of the pair $P_i,P_j$ in space, one applies to the entire configuration the rotation $A_{P_i}^{-1}$, as illustrated on the right of Figure 1, and achieves the result $A_{P_i}^{-1}{A}_{P_j}$ as the rotation in SO(3) associated to the pair $P_i,P_j$.

Figure 2 illustrates the histogram of BHBs in HQ60, where the space SO(3) of 3D rotations is depicted as a ball. To explain this, start by observing that a 3D rotation is determined by an axis L of rotation and an angle $-\pi \le \theta \le \pi$ of rotation about it, a fact that goes back to Gauss. If the unit vector $\overrightarrow{u}$ is parallel to L, then the interval of all multiples $\theta \overrightarrow{u}$ therefore corresponds to all rotations, with axis L including the trivial rotation corresponding to $\theta =0$, where $\pi \overrightarrow{u}$ and $-\pi \overrightarrow{u}$ evidently describe the same 3D rotation, namely by $\pi$ or by $-\pi$ about L.

The collection SO(3) of all 3D rotations can therefore be visualized as a 3D ball of radius $\pi$ with each pair $\pm \pi \overrightarrow{u}$ of points in its boundary 2D sphere identified to a separate single point. The particular representation in Figure 2 of the distribution in SO(3) was chosen to minimize the density proximal to the boundary. The ideal (right-handed) alpha helix has its conformational angles $\varphi =-65^{\circ }$ and $\psi =-40^{\circ }$ and here has its 3D rotation described by $\theta =1.086$, $\overrightarrow{u}=\left(-0.315,0.935,-0.164\right)$. This element of SO(3) occurs at the point of highest density in HQ60, as is evident in the middle of the fourth row from the top in Figure 2. Other local maxima for the density that are clear in the figure are studied in the cluster analysis of Penner et al. (2014).

5.3. Probabilistic methods

Table 2 provides a summary of the conformational activity of exotic residues analogous to the detailed discussion derived before from Table 1 for influenza HA, but the aligned pre- and postfusion DSSP data akin to Supplementary Table S1 for paramyxovirus, tick-borne encephalitis, and vesicular stomatitis are not presented here, only their summary in Table 2. In fact, for paramyxovirus, there only two different strains are available for pre- and postfusion conformations, which are aligned using Smith and Waterman (1981).

Table 3 presents the p-values based upon the data in Table 2. For each of the four examples, let R denote the total number of residues common to pre- and postfusion conformations, and n_a, n_b, and n_c denote the respective number of resides further than one away from an active residue, the number of active residues, and the number of inactive residues next to an active one along the backbone, respectively. The natural trinomial probability density is

$$P\left(n_a,n_b,n_c\right)=\left(\begin{array}{c}{n}_a+n_b+n_c\\ n_a{n}_b{n}_c\\ \end{array}\right){\left(\frac{a}{R}\right)}^{n_a}{\left(\frac{b}{R}\right)}^{n_b}{\left(\frac{c}{R}\right)}^{n_c}.$$

The data R, a, b, c are reported in the first four columns of Table 2 and are then used in this way to compute probabilities for the trials given in Table 3.

The computation of p-values furthermore requires a linear ordering for tails, which is also naturally given where $\left(n_a,n_b,n_c\right)\le \left(n{\prime }_a,n{\prime }_b,n{\prime }_c\right)$ provided $n_a\le n{\prime }_a$ with equality only if $n_b\ge n{\prime }_b$ with equality only if $n_c\ge n{\prime }_c$, or in other words, lexicographic ordering on triples $\left(n_a,n_b,n_c\right)$ derived from ≤ on the first and ≥ on the remaining two entries.

Call an exotic prefusion residue dissipative if its free energy is not exotic postfusion, and call it conservative otherwise, where each determination is made within one residue of the prefusion exotic residue. It is arguably only the dissipative case that provides possible false-positives in Table 3, since a conservative residue has not expended free energy presumably preserved for later conformational activity. This distinction is especially pertinent for vesicular stomatitis virus glycoprotein G, which is exceptional, as noted before, since it can oscillate back and forth between pre- and postfusion conformations.

The statistical significance for influenza and tick-borne encephalitis reported for the first p-values in Table 3 is compelling as it stands. The comparatively less significant but still acceptable first p-value for paramyxovirus likely reflects that different strains are aligned pre- and postfusion. The second p-value is tailored specifically for vesicular stomatitis to account for its conserved exotic residues evidently preserving free energy.

Disclosure Statement

No competing financial interests exist.

Funding Information

No funding was received in support of this work.

Supplementary Material

Supplementary Table S1

Supplementary Table S2

Supplementary Table S3