Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Oct 14;5(42):27546–27555. doi: 10.1021/acsomega.0c04095

A Cyclic Periodic Wave Function Approach for the Study of Infinitely Periodic Solid-State Systems. I. Application to the C–H···π(C≡C) Hydrogen Bonding Systems

Susanne Raynor 1, Hua H Song 1,*
PMCID: PMC7594129  PMID: 33134718

Abstract

graphic file with name ao0c04095_0008.jpg

The cyclic periodic wave function (CPWF) approach is applied at the AM1 and PM3 semiempirical levels of approximation to infinitely periodic solid-state systems stabilized by weak CH–pi (C–H···π) interactions between repeat units. The reliability of the AM1 and PM3 methods for modeling C–H···π bonding is first demonstrated using two representative dimer systems: the T-shaped ethyne dimer and the T-shaped propyne dimer. The CPWF method is then applied to two different crystal systems that are stabilized by C–H···π interactions: (1) pent-4-ynoic acid solid and (2) a series of three infinite crystal systems—tetrakis(4-ethynylphenyl)methane solid, tetraethynylmethane solid, and tetrabutadiynylmethane solid. A comparison of our results with available data demonstrates that the use of the CPWF approach at the AM1 and PM3 levels of approximation provides a convenient and reliable method for the study of infinitely periodic systems containing very weak C–H···π bonding.

1. Introduction

Many achievements in quantum-mechanical computations for studying infinitely periodic molecular solid-state systems have been made at different levels of ab initio and semiempirical methods since the 1970’s. The most common approaches are cluster models,1−5 cyclic cluster models (CCM),6−13 and pair-potential approaches,14−20 which are applied to study infinitely periodic molecular solid-state systems, through the use of Bloch orbitals21 and density functional theory.22,23 With the successful development of some software packages, such as the Gaussian program,24 the Vienna ab initio package (VASP),25−29 the CRYSCOR30,31 and CRYSTAL32,33 programs, and the advent of higher capacity computers, it is now relatively easy to compute the physical and chemical properties of many crystal molecules.34−38 However, it is still very challenging to study some large molecular systems computationally, such as infinite crystal solids containing weak interactions, by any of the current quantum-mechanical method, since it is necessary to use reasonably large basis sets and high-order correlation corrections simultaneously39−41 in those large molecular systems. We have developed a new ab initio cyclic periodic wave function (CPWF) method42 to solve some of the problems involved in these systems. In order for the method to be used to study reasonably large molecular systems in the crystal state, where relatively weak intermolecular interactions may be important, we will apply the method at the AM143 and PM344,45 semiempirical levels of approximation. To this end, we modified the MOPAC46 routines so that the CPWF approach could be applied at both levels of approximation.

An important consideration when applying the AM1 or PM3 methods is that they have been parameterized to generate the experimental heats of formation of many small molecules. Thus, the zero-point energies (ZPEs) of these small molecules are included implicitly, but not explicitly.

A series of studies on systems containing terminal alkynes have demonstrated that the acidic C≡C–H groups act as hydrogen bond donors to form interactions with π systems, such as C≡C–H···π (C≡C), and C≡C–H···π (Ar), or with hydroxyl groups, such as C≡C–H···O and O–H···π (C≡C).47−55 These groups form weak solid-state interactions or weak complexes. Accurate modeling of these weak interactions is critical to the understanding of the properties and characteristics of related organic crystals or molecular solids. Studies of these interactions indicate that their interaction energies are in the range of 1–3 kcal/mol and have the characteristics of weak hydrogen bonds.48,54,55

As neither AM1 nor PM3 was parameterized to replicate weak interactions, such as C–H···π interactions, we will first test these methods on some target dimers, for which ab initio calculations are available.48,49 Next, we will apply our CPWF method to two different three-dimensional crystal systems which are stabilized by these C–H···π interactions: pent-4-ynoic acid solid and a series of diamondoid crystal systems.

2. Computational Methods

The CPWF method has been described in detail in the previous paper,42 it uses the full infinite Hamiltonian operator for the crystal and begins by assuming an infinite-sized single-Slater determinant form for the ground-state wave function.

First, the infinitely periodic system is divided into chemically equivalent repeat units, where the repeat units are chosen to be either the individual molecules within molecular solids or the individual monomer units within polymers. In the CPWF approach,42 the basis set is formed from a set of cyclic periodic wave functions, and the individual repeat units are used in the complex exponential expansion, as shown in eq 1.

2. 1

Note that eq 1 is dependent upon the position indices (Ix, Iy, and Iz). These indices are chosen so that the geometric location of the center of each repeat unit can be uniquely determined from relations dependent only on its set of position indices (Ix, Iy, and Iz).

Next, repeat lengths, denoted Nx, Ny, and Nz, are selected. As explained in more detail in the previous paper,42eq 1 ensures that the cyclic periodic basis set function, ψiI, is Nx-fold periodic in the x-index, Ny-fold periodic in the y-index, and Nz-fold periodic in the z-index. The 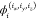Inline graphic are the atomic orbitals, which are centered in the repeat unit located at the index position (ix, iy, and iz).

Note that the complex exponential form that is used ensures that the wave function is cyclically periodic. However, this does not imply that the repeat units are cyclically periodic in their geometric positions. Instead, the repeat units are placed at their exact translationally periodic positions, as found in the infinitely periodic crystal. In this way, the CPWF approach differs from the CCM, which places the atoms or molecules at cyclic periodic positions in space.6−13

Finally, the Hartree–Fock–Roothaan approach is then used to determine the molecular orbitals, using the functions in eq 1 as the basis set functions.

In order to correct potentially misbalanced summations when finite values of Nx, Ny, and Nz are used in eq 1, we will use Raynor’s method of partitioning charge–charge interactions.56 This leads to the addition of a Madelung-like energy term, EMad, which must be added to the total electronic energy per repeat unit. Thus, the final electronic energy for repeat unit I is given by

2. 2

where EI is the energy per monomer and qα is the Mulliken charge on atom α.42,56

3. Results and Discussion

3.1. Preliminary Dimer Studies

The dimers for our initial test calculations are the ethyne dimer and the propyne dimer, both of which contain weak C≡C–H···π(C≡C) hydrogen bonding interactions. Philp and Robinson performed ab initio calculations to study the C–H···π(C≡C) interactions in three different kinds of ethyne T-shaped dimers:49 (a) the symmetrically bifurcated T-shaped ethyne dimer, as shown in Figure 1a, where the distance, x, from the donating H atom to the center of the axis of the acceptor is varied; (b) the unsymmetrically bifurcated T-shaped ethyne dimer, as shown in Figure 1b, where the distance, d, from the donating H atom to the axis of the acceptor is held constant at the optimal value, and x, the offset distance from the midpoint of the triple bond, is varied; and (c) the unsymmetrically bifurcated tilted dimer, as shown in Figure 1c, where the donating C–H bond is directed toward an individual carbon atom in the accepting triple bond. For this dimer, x represents the offset distance from the midpoint of the triple bond, and the tilt angle θ is varied.

Figure 1.

Figure 1

Open in a new tab

T-shaped ethyne dimers: (a) symmetrically bifurcated T-shaped dimer; (b) unsymmetrically bifurcated T-shaped dimer; (c) unsymmetrically bifurcated tilted dimer, with the donating C–H bond directed toward an individual carbon of the accepting triple bond; and (d) unsymmetrically bifurcated tilted dimer, with the donating C–H bond directed toward the midpoint of the accepting triple bond.

In order to compare our results directly to those of Philp and Robinson, we used the AM1 and PM3 methods to replicate the same three interactions. Although the AM1 method predicted minima at the same distances as the PM3 method, the stabilization energy from AM1 was almost negligible for these dimers. It appears that AM1, with its current parameter sets, does not properly replicate the strength of C–H···π-type stabilization in the dimer. Thus, the remaining calculations for the dimers were performed using the PM3 method.

The first dimer interaction that we studied is the symmetrically bifurcated T-shaped dimer, as shown in Figure 1a, with x varied from 2.0 to 6.8 Å, in steps of 0.1 Å or more. In the unsymmetrically bifurcated T-shaped ethyne dimer, as shown in Figure 1b, x was varied from −1.5 to +1.5 Å.

Next, in the unsymmetrically bifurcated tilted ethyne dimer, as shown in Figure 1c, the C–H···π (M) distance is held at our optimal value (where M is the midpoint of the triple bond), while the θ is varied in steps of 5 or 10°. A second set of calculations was performed for the unsymmetrically bifurcated tilted ethyne dimer in the same way, except that the donating C–H bond was directed toward the midpoint of the accepting triple bond, as shown in Figure 1d.

Similar calculations were performed for the propyne T-shaped dimer. The interaction energy in each case was then obtained from the following equation

3.1. 3

where ΔHf(d) is the calculated heat of formation for the dimer and ΔHf(m) is the calculated heat of formation for the isolated monomer. Our results for these two dimers are summarized in Table 1 and Figures 2 and 3.

Table 1. Weak Hydrogen Bonding Parameters for the T-Shaped Dimers.

T-shaped dimer ΔHIPa (kcal/mol) db (Å)
Ethyne Dimer
PM3 –1.04 2.5
ab initio(49) –1.03c 2.695
Propyne Dimer
PM3 –1.14 2.5
ab initio(48) –1.1 2.67
Open in a new tab
a

The minimum weak interaction energy for the dimer.

b

The C–H···π (M) distance for the corresponding energy, where M is the middle point of the C≡C bond.

c

Originally calculated in kJ/mol and it was converted into kcal/mol in this paper.

Figure 2.

Figure 2

Open in a new tab

Interaction potential for the symmetrically/pseudosymmetrically bifurcated T-shaped dimers; x represents the C–H···π (M) distance, where M is the midpoint of the triple bond. (a)Symmetrically bifurcated T-shaped ethyne dimer; (b) pseudo-symmetrically bifurcated T-shaped propyne dimer; and (c) symmetrically bifurcated T-shaped ethyne dimer from Philp and Robinson.49 Red ▲ Philp and Robinson’s optimal value for the ethyne dimer.49 Blue ■ Steiner et al’s optimal value for the propyne dimer.48

Figure 3.

Figure 3

Open in a new tab

Interaction potential for unsymmetrically bifurcated tilted dimers, θ is the tilt angle: (a) ethyne dimer from the ab initio method by Philp and Robinson,49 (b) propyne dimer (PM3 method with the model in Figure 1d), and (c) ethyne dimer (PM3 method with the model in Figure 1d).

Table 1 shows that our calculated results for the interaction energies are in very close agreement with ab initio calculations,48,49 to within 0.01–0.04 kcal/mol for these two dimers. In each system, our minimum interaction distances are shorter than those predicted by the ab initio calculations by ∼0.2 Å. This observation is consistent with the finding that the PM3 method generally underestimates normal hydrogen bond lengths by 0.1–0.2 Å in neutral molecules.57 Thus, once this consistent correction is applied to the hydrogen bond lengths, our results are in quite excellent agreement with the results from ab initio calculations.

The shape of the interaction potential surface for the symmetrically bifurcated T-shaped ethyne dimer from our calculations is quite similar to the corresponding surface calculated by Philp and Robinson,49 as shown in Figure 2, but these two curves do not overlap. Since Philp and Robinson calculated their interaction potential surface without the inclusion of ZPE corrections, and their ZPE-corrected results at the minimum distance are in very close agreement with those of ours, it seems likely that their surface would give energies very similar to ours, if ZPE corrections were applied. As mentioned earlier, our surface predicts the minimum to occur at a somewhat shorter distance. Thus, in general, we may expect that C–H···π interactions at the PM3 level will tend to be consistently shorter than those expected by approximately 0.1–0.2 Å.

Our calculated results for the unsymmetrically bifurcated T-shaped ethyne dimer, as shown in Figure 1b, are very similar to the symmetrically bifurcated dimer, and the results for the propyne dimer are similar to those for the ethyne dimer, in the region of small x (x < 1.0 Å). For the unsymmetrically bifurcated tilted dimer, as shown in Figure 1c, our calculated results are qualitatively different from those calculated by Philp and Robinson.49 In any case, it is more meaningful to study the effects of varying the tilt angle relative to the midpoint of the π bond in the C–H···π interactions, as this orientation is closer to the ones that occur in the crystal systems discussed later in this paper. For this reason, we selected Figure 1d as the representative of the unsymmetrically bifurcated dimer for the propyne dimer.

We repeated our calculations with the donating C–H bond directed toward the midpoint of the accepting triple bond, as shown in Figure 1d. Note that these results, shown in Figure 3, parallel those from Philp and Robinson closely, and that the addition of the ZPE corrections to their data would be expected to give a better agreement. Note that ZPE corrections are not explicitly included in PM3. However, PM3 is parameterized to generate experimental heats of formation, thus ZPEs are implicitly included.

Although we found that the PM3 method consistently underestimates the C–H···π bond length by approximately 0.1–0.2 Å, this is the same degree of underestimation that has been noticed for standard hydrogen bonds.57 With this in mind, we expect that the PM3 approximation should provide reasonably reliable interaction energies when used in combination with the CPWF approach to study crystals stabilized by C–H···π interactions.

3.2. Pent-4-ynoic Acid

The pent-4-ynoic acid solid is bound by both traditional hydrogen bonds and C–H···π type interactions.48 In the pent-4-ynoic acid solid, the carboxylic acid dimer unit was chosen as the repeat unit in the crystal, and we used a repeat length of N = 4 in each periodic direction. Our calculations for the pent-4-ynoic acid solid involved three dimensions, thus the repeat lengths are Nx = Ny = Nz = 4, and Δix = Δiy = Δiz = −1, 0, 1. This gives a total of 27 possible combinations for the position indices. Using the spatial symmetry of the pent-4-ynoic acid crystal solid, we calculated the interaction distances that would occur between the repeat units at 000 with those at each of the 27 index positions. We then retained all terms which involved contacts that were shorter than 4.9 Å.

For the application of the CPWF approach, we began by optimizing the geometry in an isolated carboxylic acid dimer unit and then used this optimal geometry as the initial trial geometry for the dimer in the full crystal calculations. Calculations were performed at both the AM1 and PM3 levels of approximation. Our initial interdimer interaction parameters were obtained from the X-ray crystallographic data of Steiner et al.(48) A full geometry optimization of both intramonomer and intermonomer geometry parameters was then performed. The heat of formation for the solid was evaluated at the minimum geometry, and the interaction energy was then calculated from the following equation

3.2. 4

where ΔHf(s) is the calculated heat of formation for the pent-4-ynoic acid solid and ΔHf(d) is the calculated heat of formation for the isolated dimer unit. As each dimer unit forms four hydrogen bonds with other monomers, each monomer donates a total of two hydrogen bonds to the crystal structure. The net energy per hydrogen bond, ΔHH, thus becomes

3.2. 5

Our results are summarized in Tables 2 and 3, and the final calculated crystal structure for the pent-4-ynoic acid solid is shown in Figure 4.

Table 2. Weak Hydrogen Bond Parameters for Pent-4-ynoic Acid Solid.

pent-4-ynoic acid da (Å) C···Hb (Å) C–H···Mc (°) ΔHf(d)d (kcal/mol) ΔHf(s)e (kcal/mol) ΔHIPf (kcal/mol) ΔHHg (kcal/mol)
PM3 2.5 2.5 174 –112.93 –117.43 –4.50 –2.25
    2.5          
AM1 2.6 2.7 165 –113.67 –117.08 –3.41 –1.71
    2.6          
experimental data48 2.69 2.76 155        
    2.74          
ab initio(48) 2.67 2.75 159       –2.1
    2.71          
Open in a new tab
a

C-H···π (M) distance, where M is the middle point of the C≡C bond.

b

The distance between the donating H atom and both C atoms in the C≡C bond.

c

The weak hydrogen bond angle, where M is the middle point of the C≡C bond.

d

The heat of formation for the isolated dimer unit.

e

The heat of formation for the solid.

f

The total interaction energy.

g

The net interaction energy per hydrogen bond.

Table 3. Optimal Unit Cell Parameters for Pent-4-ynoic Acid Solid.

pent-4-ynoic acid solid a (Å) b (Å) c (Å) α (deg) β (deg) γ (deg)
PM3 7.3 5.8 27.3 90 90 90
AM1 7.6 5.3 27.1 90 90 90
experimental data48 6.862(1) 5.7465(7) 27.192(8) 90 90 90
Open in a new tab

Figure 4.

Figure 4

Open in a new tab

Crystal structure of pent-4-ynoic acid solid from PM3 level results.

From Table 2, we see that our predicted energy per hydrogen bond for the pent-4-ynoic acid solid is −2.25 kcal/mol, with a C–H···π (M) distance of 2.5 Å at the PM3 level of approximation, and is −1.71 kcal/mol with a C–H···π (M) distance of 2.6 Å at the AM1 level of approximation. Steiner et al.(48) estimated the energy for the hydrogen bond to be about −2.1 kcal/mol with a C–H···π (M) distance of 2.67 Å, using the ab initio MO LCAO SCF (HF + MP2) calculations. We see that our PM3 energies are in good agreement with those of Steiner’s, but the bond length was underestimated by 0.1–0.2 Å, which is consistent with its performance on the dimer systems. We can conclude that the PM3 calculations for the pent-4-ynoic acid solid were very successful. The AM1 level calculations predicted a weaker bond interaction (by about 0.4 kcal/mol) and a bond length that is shorter by 0.1 Å when compared to Steiner’s results. Although AM1 predicts a slightly weaker C–H···π energy than that expected for these systems, it predicts C–H···π bond lengths that are closer to those predicted by Steiner et al.(48)

Table 3 shows a comparison of our calculated cell dimensions to the experimental values of Steiner et al.(48) Both methods yield very reasonable values for all three dimensions. However, the PM3 values are in better agreement with the experimental values, specifically in the b and c dimensions. Therefore, our calculations for pent-4-ynoic acid demonstrate that the novel CPWF approach at both AM1 and PM3 levels of approximation successfully replicates the weak C–H···π interactions and structure of pent-4-ynoic acid.

3.3. Diamondoid Crystal Solids

The first one studied in the series of diamondoid crystal systems is the tetrakis(4-ethynylphenyl)methane crystal solid, which is the first diamondoid network discovered to be linked by C≡C–H···π(C≡C) interactions.47 In this system, each monomer comprises four “arms” attached nearly tetrahedrally to a central carbon atom, and each arm consists of a phenyl group followed by an acetylene group (4-ethynylphenyl group). In addition to this system, we will also perform calculations on two potential derivatives of this system: tetraethynylmethane solid and tetrabutadiynylmethane solid. The tetraethynylmethane solid has been synthesized,58,59 but its structure could not be determined experimentally. The tetrabutadiynylmethane solid has not yet been synthesized experimentally. As experimental data are available only for the tetrakis(4-ethynylphenyl)methane diamondoid crystal solid, we will assume that all the diamondoid crystal systems crystallize in the same space group and are stabilized by similar C–H···π-type interactions (C≡C–H···π(C≡C)) between their repeat units, and use the available experimental data of the tetrakis(4-ethynylphenyl)methane solid47 for all the three diamondoid crystal systems in our series of calculations.

In each of the three diamondoid crystal solids, the individual molecule is chosen as the repeat unit in the crystal. As calculations for the tetrakis(4-ethynylphenyl)methane solid involves three dimensions, the repeat lengths are again Nx = Ny = Nz = 4, thus Δix = Δiy = Δiz = −1, 0, 1. The position indices for all the important attractive or repulsive interactions in the matrix elements are determined by the space group of tetrakis(4-ethynylphenyl)methane solid.

These interactions are the ones responsible for all eight of the C–H···π interactions experienced by any one molecule, since each “arm” of the molecule acts both as a donor for a C–H···π interaction with one molecule and as an acceptor from another. All the excluded interactions involved contacts that were longer than 3.5 Å.

Note, however, that the X-ray crystallographic studies of Galoppini and Gilardi47 showed that the tetrakis(4-ethynylphenyl)methane solid crystal consists of three interconnected networks which are stabilized by π···π stacking interactions. These π···π interactions cannot be properly replicated at the AM1 or PM3 levels of approximation, so we confined our calculations to the study of a single network.

Our calculations on tetrakis(4-ethynylphenyl)methane were done in two steps. First, we determined the optimal geometry for the isolated monomer, using its experimental geometry as our initial trial geometry. Next, we performed calculations on the full three-dimensional crystal and allowed all geometric parameters to vary.

We then performed similar calculations on the monomers and solids for the tetraethynylmethane crystal and the tetrabutadiynylmethane crystal.

The interaction energies for the solids in each case were then calculated from the following equation

3.3. 6

where ΔHf(s) is the calculated heat of formation for the solid and ΔHf(m) is the calculated heat of formation for its corresponding monomer. The net energy per weak hydrogen bond is then calculated as follows

3.3. 7

as each molecule is involved in sharing eight C–H···π interactions.

Our final data for the weak hydrogen bond and the optimal solid geometries are given in Tables 4–6 and Figures 5 and 6.

Table 4. Weak Hydrogen Bond Geometry Parameters for Diamondoid Solids.

crystal solid da(Å) C···Hb (Å) C–H···Mc (deg)
Tetrakis(4-ethynylphenyl)methane
PM3 2.5 2.6 2.7 130
AM1 2.7 2.5 3.0 149
experimental data47 2.86 2.76 3.08 140.1
Tetraethynylmethane
PM3 2.5 2.5 2.7 141
AM1 2.6 2.5 2.8 146
Tetrabutadiynylmethane
PM3 2.5 2.5 2.7 137
AM1 2.6 2.6 2.7 135
Open in a new tab
a

C–H···π (M) distance, where M is the middle point of the C≡C bond.

b

the distance between the donating H atom and both C atoms in the C≡C bond.

c

The weak hydrogen bond angle, where M is the middle point of the C≡C bond.

Table 6. Optimal Unit Cell Parameters for the Selected Diamondoid Solids.

crystal solid a (Å) b (Å) c (Å) α (deg) β (deg) γ (deg)
Tetrakis(4-ethynylphenyl)methane
PM3 12.6 12.6 7.1 90 90 90
AM1 13.5 13.5 7.2 90 90 90
experimental data47 12.9197(4) 12.9197(4) 7.2357(5) 90 90 90
Tetraethynylmethane
PM3 7.5 7.5 3.1 90 90 90
AM1 7.7 7.7 3.1 90 90 90
Tetrabutadiynylmethane
PM3 11.2 11.2 5.1 90 90 90
M1 11.2 11.2 5.1 90 90 90
Open in a new tab

Figure 5.

Figure 5

Open in a new tab

Crystal structure of tetrakis(4-ethynylphenyl)methane solid from PM3 level results. Heavy lines indicate the shorter of the two C···H atomic pair distances and lighter lines indicate the longer of the distances.

Figure 6.

Figure 6

Open in a new tab

(a) Predicted crystal structure of tetraethynylmethane solid. Dashed lines show C···H interactions. Heavy lines indicate the shorter of the two C···H atomic pair distances and lighter lines indicate the longer of the distances. (b) Predicted crystal structure of tetraethynylmethane solid showing the three interwoven diamondoid nets.

As shown in Table 5, AM1 systematically underpredicts the strength of C–H···π interactions, which is consistent with our results for the test dimer interactions. Thus, we will primarily focus on the comparison of our PM3 energetic results with the experimental ones. As shown in Tables 4 and 5, the predicted weak hydrogen bond energy for the tetrakis(4-ethynylphenyl)methane solid is −1.21 kcal/mol at a C–H···π (M) distance of 2.5 Å. Since, as previously observed, calculations at the PM3 level of approximation underestimate C–H···π bond lengths by 0.1–0.2 Å, this compares well with the experimental C–H···π (M) distance of 2.86 Å.47

Table 5. Weak Hydrogen Bond Energies for Diamondoid Solids.

crystal solid ΔHf(m)a(kcal/mol) ΔHf(s)b(kcal/mol) ΔHIPc(kcal/mol) ΔHHd(kcal/mol)
Tetrakis(4-ethynylphenyl)methane
PM3 321.10 316.26 –4.84 –1.21
AM1 336.15 334.48 –1.67 –0.42
Tetraethynylmethane
PM3 211.75 207.40 –4.35 –1.09
AM1 228.77 226.81 –1.96 –0.49
Tetrabutadiynylmethane
PM3 419.42 415.75 –3.67 –0.92
AM1 436.06 434.61 –1.45 –0.36
Open in a new tab
a

The heat of formation for the monomer.

b

The heat of formation for the solid.

c

The total interaction energy.

d

The net interaction energy per weak hydrogen bond.

All three diamondoid crystals are predicted to have similar hydrogen bond energies. However, there appears to be a slight trend occurring in their relative stabilities, that is, the tetrakis(4-ethynylphenyl)methane solid is predicted to be most stable with a hydrogen bond energy of 1.21 kcal/mol, and the tetrabutadiynylmethane solid is predicted to be least stable with a hydrogen bond energy of 0.92 kcal/mol.

However, the slight differences in the weak hydrogen bonding energies between the tetrakis(4-ethynylphenyl)methane solid and the tetraethynylmethane solid are unlikely to be the reason why the tetraethynylmethane solid is unstable at room temperature.58,59 It is likely that the tetrakis(4-ethynylphenyl)methane solid is further stabilized by π–π stacking among its three intertwined networks because of the presence of phenyl groups in its crystal structure. These π–π stacking interactions may account for the greater stability of the tetrakis(4-ethynylphenyl)methane solid over the other two crystal systems.

From Table 5, it can be seen that the hydrogen bond energy for the tetrabutadiynylmethane solid is slightly weaker than those for both the tetrakis(4-ethynylphenyl)methane solid and tetraethynylmethane solid. No one has yet published any experimental data for the tetrabutadiynylmethane solid. However, Guo et al.(60) synthesized a similar tetrahedral compound, in which the terminal 1,3-diyne replaces ethyne in the tetrakis(4-ethynylphenyl)methane solid.60 They found that this compound, tetrakis(4-1,3-diynylphenyl)methane solid, could not be isolated in its pure form and decomposed when ethyne was deprotected.60 Based on this fact and considering that its hydrogen bond energy is predicted to be even weaker than that for the tetraethynylmethane solid, it seems likely that the pure tetrabutadiynylmethane solid would be either unstable or at best very difficult to synthesize. In addition, the tetrabutadiynylmethane solid may polymerize to form a parallel structure between the 1,3-diacetylenic groups, as it occurs in similar systems.61−66

Finally, from Table 6, the unit cell parameters calculated at both AM1 and PM3 levels of approximation for the tetrakis(4-ethynylphenyl)methane solid are seen to be in very close agreement with the experimental data of Galoppini and Gilardi.47 The predicted cell dimensions for the related solids, tetraethynylmethane solid and tetrabutadiynylmethane solid, are smaller than that for the tetrakis(4-ethynylphenyl)methane solid, as expected, because their monomers are substantially smaller.

4. Conclusions

Our calculation results at the PM3 level of approximation agree very well with the available experimental and ab initio data. Thus, at the PM3 level of approximation, the CPWF approach should provide a very reliable model to study the electronic structure of systems containing C–H···π-type weak hydrogen bonds. Although the AM1 method underestimates the strength of the C–H···π bond, it nonetheless predicted reasonable geometries for the solid-state systems studied here.

In conclusion, the CPWF approach at the AM1 and PM3 levels of approximation provides a convenient and reliable method for the study of infinitely periodic systems containing very weak C–H···π bonding.

Acknowledgments

The authors are grateful to Professor Roger A. Lalancette for his valuable time in helping them generate Figures 4–6.

Author Present Address

† Pfizer Inc., 400 Webro Road, Parsippany, NJ 07054, USA.

The authors declare no competing financial interest.

References

  1. Watkins G. D.; Messmer R. P.. Computational Methods For Large Molecules And Localized States In Solids; Herman F., McLean A. D., Nesbet R. K., Eds.; Plenum Press: New York-London, 1973; pp 133–147. [Google Scholar]
  2. Messmer R. P.; Watkins G. D. Molecular-orbital Treatment for Deep Levels in Semiconductors. Substitutional Nitrogen and the Lattice Vacancy in Diamond. Phys. Rev. B: Solid State 1973, 7, 2568–2590. 10.1103/physrevb.7.2568. [DOI] [Google Scholar]
  3. Turi L.; Dannenberg J. J. Molecular Orbital Study of Crystalline Acetic Acid. 2. Aggregates in One, Two, and Three Dimensions. J. Am. Chem. Soc. 1994, 116, 8714–8721. 10.1021/ja00098a034. [DOI] [Google Scholar]
  4. Raynor S. Importance of High-order Interactions in Models of Molecular Solids at High Pressure. J. Chem. Phys. 1989, 91, 7018–7023. 10.1063/1.457318. [DOI] [Google Scholar]
  5. Wieczorek R.; Dannenberg J. J. H-Bonding Cooperativity and Energetics of α-Helix Formation of Five 17-Amino Acid Peptides. J. Am. Chem. Soc. 2003, 125, 8124–8129. 10.1021/ja035302q. [DOI] [PubMed] [Google Scholar]; , and refs therein
  6. Zunger A. A Molecular Calculation of Electronic Properties of Layered Crystals: II. Periodic Small Cluster Calculation for Graphite and Boron Nitride. J. Phys. C: Solid State Phys. 1974, 7, 96–106. 10.1088/0022-3719/7/1/017. [DOI] [Google Scholar]
  7. Zunger A. Small Periodic Cluster Calculation on Point Defect Problems in Hexagonal Layered Solids. J. Chem. Phys. 1975, 62, 1861–1868. 10.1063/1.430670. [DOI] [Google Scholar]
  8. Zunger A.; Katzir A. Point Defects in Hexagonal Boron Nitride. II. Theoretical Studies. Phys. Rev. B: Solid State 1975, 11, 2378–2390. 10.1103/physrevb.11.2378. [DOI] [Google Scholar]
  9. Bredow T.; Evarestov R. A.; Jug K. Implementation of the Cyclic Cluster Model in Hartree-Fock LCAO Calculations of Crystalline Systems. Phys. Status Solidi B 2000, 222, 495–516. . [DOI] [Google Scholar]
  10. Bredow T.; Geudtner G.; Jug K. Development of the Cyclic Cluster Approach for Ionic Systems. J. Comput. Chem. 2001, 22, 89–101. . [DOI] [Google Scholar]
  11. Janetzko F.; Bredow T.; Jug K. Effects of Long-range Interactions in Cyclic Cluster Calculations of Metal Oxides. J. Chem. Phys. 2002, 116, 8994–9004. 10.1063/1.1473802. [DOI] [Google Scholar]
  12. Janetzko F.; Evarestov R. A.; Bredow T.; Jug K. First-principles Periodic and Semiempirical Cyclic Cluster Calculations for Single Oxygen Vacancies in Crystalline Al2O3. Phys. Status Solidi B 2004, 241, 1032–1040. 10.1002/pssb.200301961. [DOI] [Google Scholar]
  13. Janetzko F.; Köster A. M.; Salahub D. R. Development of the Cyclic Cluster Model Formalism for Kohn-Sham Auxiliary Density Function Theory Methods. J. Chem. Phys. 2008, 128, 024102-1–024102-14. 10.1063/1.2817582. [DOI] [PubMed] [Google Scholar]
  14. Ree F. H.; Bender C. F. Nonadditive Interaction in Molecular Hydrogen at High Pressure. Phys. Rev. Lett. 1974, 32, 85–88. 10.1103/physrevlett.32.85. [DOI] [Google Scholar]
  15. Etters R. D.; Danilowicz R.; England W. Properties of Solid and Gaseous Hydrogen, Based upon Anisotropic Pair Interactions. Phys. Rev. A 1975, 12, 2199–2212. 10.1103/physreva.12.2199. [DOI] [Google Scholar]
  16. LeSar R.; Herschbach D. R. Likelihood of a High-Pressure Phase of Solid Hydrogen Involving Termolecular Complexes. J. Phys. Chem. A 1981, 85, 3787–3792. 10.1021/j150625a016. [DOI] [Google Scholar]
  17. Nozawa K.; Shima N.; Makoshi K. Theoretical Calculations for Solid Oxygen under High Pressure. J. Phys.: Condens. Matter 2008, 20, 335219/1–335219/6. 10.1088/0953-8984/20/33/335219. [DOI] [Google Scholar]
  18. Kumar V. Icosahedral Symmetry in Clusters. Prog. Cryst. Growth Charact. Mater. 1997, 34, 95–131. 10.1016/s0960-8974(97)00007-7. [DOI] [Google Scholar]
  19. Hay P. J.; Pack R. T.; Martin R. L. Electron Correlation Effects on the Molecular Nitrogen-Molecular Nitrogen interaction. J. Chem. Phys. 1984, 81, 1360–1372. 10.1063/1.447770. [DOI] [Google Scholar]
  20. Hinde R. J.Computational Vibrational Spectroscopy of H2 Aggregates: Quantifying the Role of the Three-body Interactions. Abstracts of Papers, 235th ACS National Meeting, New Orleans, LA, United States, April 6–10, 2008. PHYS-049.
  21. Bloch F. Quantum Mechanics of Electrons in Crystals. Z. Phys. 1928, 52, 555–599. [Google Scholar]
  22. Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. 10.1103/physrev.136.b864. [DOI] [Google Scholar]
  23. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. 10.1103/physrev.140.a1133. [DOI] [Google Scholar]
  24. Hehre W. J.; Stewart R. F.; Pople J. A. Self-consistent Molecular-orbital Methods. I. Use of Gaussian Expansions of Slater-type Atomic Orbitals. J. Chem. Phys. 1969, 51, 2657–2664. 10.1063/1.1672392. [DOI] [Google Scholar]; ; and the series of articles for the GAUSSIAN program package afterwards
  25. Kresse G.; Hafner J. ab initio Molecular Dynamics for Open-shell Transition Metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 48, 13115–13118. 10.1103/physrevb.48.13115. [DOI] [PubMed] [Google Scholar]
  26. Kresse G.; Hafner J. ab initio Molecular-dynamics Simulation of the Liquid-metal-amorphous-semiconductor Transition in Germanium. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49, 14251–14269. 10.1103/physrevb.49.14251. [DOI] [PubMed] [Google Scholar]
  27. Kresse G.; Furthmüller J. Efficiency of ab-initio Total Energy Calculations for Metals and Semiconductors Using a Plane-wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  28. Kresse G.; Furthmüller J. J Efficient Iterative Schemes for ab initio Total-energy Calculations Using a Plane-wave Basis Set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
  29. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/physrevb.59.1758. [DOI] [Google Scholar]
  30. Erba A.; Halo M.. CRYSCOR09 User’s Manual; University of Torino: Torino, 2009. (www.cryscor.unito.it).
  31. Pisani C.; Schütz M.; Casassa S.; Usvyat D.; Maschio L.; Lorenz M.; Erba A. CRYSCOR: a Program for the Post-Hartree-Fock Treatment of Periodic Systems. Phys. Chem. Chem. Phys. 2012, 14, 7615–7628. 10.1039/c2cp23927b. [DOI] [PubMed] [Google Scholar]
  32. Dovesi R.; Saunders V. R.; Roetti C.; Orlando R.; Zicovich-Wilson C. M.; Pascale F.; Civalleri B.; Doll K.; Harrison N. M.; Bush I. J.; D’Arco P.; Llunell M.; Causà M.; Noël Y.; Maschio L.; Erba A.; Rerat M.; Casassa S.. CRYSTAL17 User’s Manual; University of Torino: Torino, 2017.
  33. Dovesi R.; Erba A.; Orlando R.; Zicovich-Wilson C. M.; Civalleri B.; Maschio L.; Rérat M.; Casassa S.; Baima J.; Salustro S.; Kirtman B. Quantum-mechanical Condensed Matter Simulations with CRYSTAL. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1360 10.1002/wcms.1360. [DOI] [Google Scholar]; , and references therein
  34. Sun G.; Kürti J.; Rajczy P.; Kertesz M.; Hafner J.; Kresse G. Performance of the Vienna ab initio Simulation Package (VASP). J. Mol. Struct.: THEOCHEM 2003, 624, 37–45. 10.1016/s0166-1280(02)00733-9. [DOI] [Google Scholar]
  35. Hafner J. Materials Simulations Using VASP – A Quantum Perspective to Materials Science. Comput. Phys. Commun. 2007, 177, 6–13. 10.1016/j.cpc.2007.02.045. [DOI] [Google Scholar]
  36. Kleis J.; Lundqvist B. I.; Langreth D. C.; Schröder E. Towards a Working Density-functional Theory for Polymers: First-principles Determination of the Polyethylene Crystal Structure. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 76, 100201-1–100201-4. 10.1103/physrevb.76.100201. [DOI] [Google Scholar]
  37. Bučko T.; Hafner J.; Lebègue S.; Ángyán J. G. Improved Description of the Structure of Molecular and Layered Crystals: Ab Initio DFT Calculations with van der Waals Corrections. J. Phys. Chem. A 2010, 114, 11814–11824. [DOI] [PubMed] [Google Scholar]
  38. Lehtola S.; Jónsson E. Ö.; Jónsson H. Effect of Complex-Valued Optimal Orbitals on Atomization Energies with the Perdew-Zunger Self-interaction Correction to Density Functional Theory. J. Chem. Theory Comput. 2016, 12, 4296–4302. 10.1021/acs.jctc.6b00622. [DOI] [PubMed] [Google Scholar]
  39. Fink K.; Staemmler V. Ab initio Calculations of van der Waals Interactions in One- and Two-Dimensional Infinite Periodic Systems. J. Chem. Phys. 1995, 103, 2603–2614. 10.1063/1.470521. [DOI] [Google Scholar]
  40. Delhalle J.; Piela L.; Brédas J.-L.; André J.-M. Multipole Expansion in Tight-Binding Hartree-Fock Calculations for Infinite Model Polymers. Phys. Rev. B: Condens. Matter Mater. Phys. 1980, 22, 6254–6267. 10.1103/physrevb.22.6254. [DOI] [Google Scholar]
  41. Pisani C.; Dovesi R.; Roetti C.. Lecture Notes in Chemistry, Hartree–Fock Ab initio Treatment of Crystalline Systems; Berthier G., Dewar M. J. S., Fischer H., Fukui K., Hall G. G., Hinze J., Jaffé H. H., Jortner J., Kutzelnigg W., Ruedenberg K., Tomasi J.. Springer-Verlag, 1988; Vol. 48; p 5. [Google Scholar]
  42. Raynor S.; Song H. H.. Development of a Cyclic Periodic Wave Function Approach for the Study of Infinitely-Periodic Solid-State Systems. ACS Omega. 2020, 10.1021/acsomega.0c04094. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Dewar M. J. S.; Zoebisch E. G.; Healy E. F.; Stewart J. J. P. Development and Use of Quantum Mechanical Molecular Models. 76. AM1: A New General Purpose Quantum Mechanical Molecular Model. J. Am. Chem. Soc. 1985, 107, 3902–3909. 10.1021/ja00299a024. [DOI] [Google Scholar]
  44. Stewart J. J. P. Optimization of Parameters for Semiempirical Methods. I. Method. J. Comput. Chem. 1989, 10, 209–220. 10.1002/jcc.540100208. [DOI] [Google Scholar]
  45. Stewart J. J. P. Optimization of Parameters for Semiempirical Methods. II. Applications. J. Comput. Chem. 1989, 10, 221–264. 10.1002/jcc.540100209. [DOI] [Google Scholar]
  46. Stewart J. J. P.QCPE 455, (Quantum Chemistry Program Exchange); Chemistry Department, Indiana University: Bloomington, IN.
  47. Galoppini E.; Gilardi R. Weak Hydrogen Bonding Between Acetylenic Groups: the Formation of Diamondoid Nets in the Crystal Structure of Tetrakis(4-ethynylphenyl)methane. Chem. Commun. 1999, 2, 173–174. 10.1039/a807993e. [DOI] [Google Scholar]
  48. Steiner T.; Starikov E. B.; Amado A. M.; Teixeira-Dias J. J. C. Weak Hydrogen Bonding. Part 2. The Hydrogen Bonding Nature of Short C-H···π Contacts: Crystallographic, Spectroscopic and Quantum Mechanical Studies of Some Terminal Alkynes. J. Chem. Soc., Perkin Trans. 2 1995, 1321–1326. 10.1039/p29950001321. [DOI] [Google Scholar]
  49. Philp D.; Robinson J. M. A. A Computational Investigation of Cooperativity in Weakly Hydrogen-Bonded Assemblies. J. Chem. Soc., Perkin Trans. 2 1998, 1643–1650. 10.1039/a800931g. [DOI] [Google Scholar]
  50. Steiner T.; Tamm M.; Grzegorzewski A.; Schulte N.; Veldman N.; Schreurs A. M. M.; Kanters J. A.; Kroon J.; van der Maas J.; Lutz B. Weak Hydrogen Bonding. Part 5. Experimental Evidence for the Long-Range Nature of C≡C-H···π Interactions: Crystallographic and Spectroscopic Studies of Three Terminal Alkynes. J. Chem. Soc., Perkin Trans. 2 1996, 2441–2446. 10.1039/p29960002441. [DOI] [Google Scholar]
  51. Robinson J. M. A.; Kariuki B. M.; Gough R. J.; Harris K. D. M.; Philp D. Preferential Formation of C≡C-H···π(C≡C) Interactions in the Solid State. J. Solid State Chem. 1997, 134, 203–206. 10.1006/jssc.1997.7646. [DOI] [Google Scholar]
  52. Weiss H.-C.; Bläser D.; Boese R.; Doughan B. M.; Haley M. M. C-H···π Interactions in Ethynylbenzenes: the Crystal Structures of Ethynylbenzene and 1,3,5-triethynylbenzene, and a Redetermination of the Structure of 1,4-diethynylbenzene. Chem. Commun 1997, 1703–1704. 10.1039/a704070i. [DOI] [Google Scholar]
  53. Starikov E. B.; Saenger W.; Steiner T. Quantum Chemical Calculations on the Weak Polar Host-Guest Interactions in Crystalline Cyclomaltoheptaose (β-cyclodextrin)-but-2-yne-1,4-diol heptahydrate. Carbohydr. Res. 1998, 307, 343–346. 10.1016/s0008-6215(98)00022-6. [DOI] [Google Scholar]
  54. Steiner T. Reviews: The Hydrogen Bond in the Solid State. Angew. Chem., Int. Ed. 2002, 41, 48–76. . [DOI] [PubMed] [Google Scholar]
  55. Sánchez-García E.; George L.; Montero L. A.; Sander W. 1:2 Formic Acid/Acetylene Complexes: Ab Initio and Matrix Isolation Studies of Weakly Interacting Systems. J. Phys. Chem. A 2004, 108, 11846–11854. 10.1021/jp0485082. [DOI] [Google Scholar]
  56. Raynor S. Avoiding Truncation Errors in Hartree-Fock Theories of Periodic Systems. J. Chem. Phys. 1991, 94, 2940–2945. 10.1063/1.459816. [DOI] [Google Scholar]
  57. Jurema M. W.; Shields G. C. Ability of the PM3 Quantum-Mechanical Method to Model Intermolecular Hydrogen Bonding Between Neutral Molecules. J. Comput. Chem. 1993, 14, 89–104. 10.1002/jcc.540140113. [DOI] [Google Scholar]
  58. Feldman K. S.; Kraebel C. M.; Parvez M. Tetraethynylmethane. J. Am. Chem. Soc. 1993, 115, 3846–3847. 10.1021/ja00062a089. [DOI] [Google Scholar]
  59. Amemiya R.; Suwa K.; Toriyama J.; Nishimura Y.; Yamaguchi M. One-step Synthesis of Triethynylvinylmethanes and Tetraethynylmethanes by GaCl3-Promoted Diethynylation of 1,4-enynes and 1,4-diynes. J. Am. Chem. Soc. 2005, 127, 8252–8253. 10.1021/ja051416l. [DOI] [PubMed] [Google Scholar]
  60. Guo W.; Galoppini E.; Gilardi R.; Rydja G. I.; Chen Y.-H. Weak Intermolecular Interactions in the Crystal Structures of Molecules with Tetrahedral Symmetry: Diamondoid Nets and Other Motifs. Cryst. Growth Des. 2001, 1, 231–237. 10.1021/cg005531d. [DOI] [Google Scholar]
  61. Enkelmann V. Structural Aspects of the Topochemical Polymerization of Diacetylenes. Adv. Polym. Sci. 1984, 63, 91–136. 10.1007/bfb0017652. [DOI] [Google Scholar]
  62. Baughman R. H. Solid-State Synthesis of Large Polymer Single Crystals. J. Polym. Sci., Polym. Phys. Ed. 1974, 12, 1511–1535. 10.1002/pol.1974.180120801. [DOI] [Google Scholar]
  63. Price W. S.; Kikuchi N.; Matsuda H.; Hayamizu K.; Okada S.; Nakanishi H. Factors Affecting the Solid-State Polymerization of 1,4-Bis(1,3-octadecadiynyl)Benzene to a Polydiacetylene. Macromolecules 1995, 28, 5363–5369. 10.1021/ma00119a029. [DOI] [Google Scholar]
  64. Kane J. J.; Liao R.-F.; Lauher J. W.; Fowler F. W. Preparation of Layered Diacetylenes as a Demonstration of Strategies for Supramolecular Synthesis. J. Am. Chem. Soc. 1995, 117, 12003–12004. 10.1021/ja00153a026. [DOI] [Google Scholar]
  65. Ouyang X.; Fowler F. W.; Lauher J. W. Single-Crystal-to-Single-Crystal Topochemical Polymerizations of a Terminal Diacetylene: Two Remarkable Transformations Give the Same Conjugated Polymer. J. Am. Chem. Soc. 2003, 125, 12400–12401. 10.1021/ja037557+. [DOI] [PubMed] [Google Scholar]
  66. Nagahama S.; Inoue K.; Sada K.; Miyata M.; Matsumoto A. Two-Dimensional Hydrogen Bond Networks Supported by CH/π Interaction Leading to a Molecular Packing Appropriate for Topochemical Polymerization of 1,3-Diene Monomers. Cryst. Growth Des. 2003, 3, 247–256. 10.1021/cg020070c. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES