Abstract
In the test-negative design, routine testing at health-care facilities is leveraged to estimate the effectiveness of an intervention such as a vaccine. The odds of vaccination for individuals who test positive for a target pathogen is compared with the odds of vaccination for individuals who test negative for that pathogen, adjusting for key confounders. The design is rapidly growing in popularity, but many open questions remain about its properties. In this paper, we examine temporal confounding by generalizing derivations to allow for time-varying vaccine status, including out-of-season controls, and open populations. We confirm that calendar time is an important confounder when vaccine status varies during the study. We demonstrate that, where time is not a confounder, including out-of-season controls can improve precision. We generalize these results to open populations. We use our theoretical findings to interpret 3 recent papers utilizing the test-negative design. Through careful examination of the theoretical properties of this study design, we provide key insights that can directly inform the implementation and analysis of future test-negative studies.
Keywords: case-control studies, confounding factors, seasonal variation, test-negative design, vaccination
Abbreviations
- VE
vaccine effectiveness
The test-negative design is a recent epidemiologic design (1, 2). Resembling a case-control study but structured as an indirect cohort (3), the test-negative design enrolls individuals presenting at health-care facilities with a particular clinical syndrome. Each individual is tested for the vaccine-targeted pathogen(s) using a sensitive and specific laboratory test. Individuals who test negative serve as controls for individuals who test positive. Vaccine effectiveness (VE) is estimated as 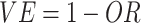 , where
, where 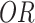 is the odds ratio for exposure to vaccination for test-positive cases versus test-negative controls, adjusting for key confounders. Under standard assumptions, the odds ratio estimates the population relative risk (4).
is the odds ratio for exposure to vaccination for test-positive cases versus test-negative controls, adjusting for key confounders. Under standard assumptions, the odds ratio estimates the population relative risk (4).
The test-negative design has several key advantages over other observational studies. They are substantially cheaper and easier to implement than cohort studies. They can be readily integrated into routine surveillance for passive detection of cases. Unlike a traditional case-control study, the control population is naturally defined from the test negatives, precluding the need for external sampling of controls. There might be complex reasons why certain cases present for testing, including differential access to care. By restricting to individuals who seek health care and are tested, the test-negative design reduces (although might not eliminate) confounding due to health-care seeking behavior (5, 6). Test-negative designs have been widely used in the assessment of influenza vaccines (1, 7) and have been applied to cholera (8, 9) and rotavirus (10).
Work is ongoing to examine the theoretical underpinnings of the test-negative design (1, 2, 5, 11, 12). The central assumption is that vaccine has no effect on other causes of the same clinical syndrome. Thus, the test-negative controls serve as a proxy for estimating the distribution of vaccine in the underlying population. Other key assumptions include no residual confounding after adjusting for measured confounders and accurate diagnostics.
Previous statistical work to assess the unbiasedness of the test-negative design odds-ratio estimator for the true vaccine effect has focused on closed populations, fixed (non-time-varying) vaccination status, and constant test-positive and test-negative hazard rates, although 2 papers briefly considered time-varying rates (11, 12). Earlier work has demonstrated that, in a closed population where vaccination is completed before the study’s start, the test-negative design odds ratio is unbiased for the all-or-none vaccine effect even when the hazard rates vary over time (11, 12). For all-or-none vaccines, the relative risk is time-invariant and is the target estimand for the vaccine effect (13, 14). Thus, time is not a confounder if a vaccination campaign is completed before the start of a season (15). Where vaccine uptake continues during the season, though, calendar time is likely an important confounder. Adjusting for time was essential when analyzing data from the 2009 H1N1 influenza pandemic because vaccine was provided responsively (16). This has been demonstrated by simulation (17) but has not been confirmed theoretically.
Another important consideration is how to handle test-negative controls observed when the target disease is not circulating (“out of season”). These might be collected before or after the season, or from interim weeks when no cases are detected. Jackson and Nelson (1) suggest that these controls induce immortal person-time bias; a common practice is to exclude them from the analysis (7), despite others arguing that excluding these individuals is not necessary if all vaccinations have been provided before the start of recruitment (15). Data analyses (18) and simulations (17) have noted little impact of restricting to only weeks with cases, after adjusting for time. Nonetheless, the inclusion/exclusion of out-of-season controls remains an important open question with no theoretical results to guide decision-making.
All prior theoretical and simulation studies have focused on closed populations. In practice, individuals will age into and out of the target population or move in or out of the study area. For infant vaccines, such as the rotavirus vaccine, an open population is particularly relevant because children are born during the course of the study.
We address open questions about temporal confounding due to time-varying vaccination status, out-of-season controls, and open populations. Below, we derive results that allow for generic test-positive and test-negative hazard rates, and we consider a generic vaccine rollout strategy that allows coverage to change during the study. We consider an open population such as separate birth cohorts. Importantly, we provide a theoretical basis for many results that have previously been evaluated in simulation only. We apply these findings to recent papers on the test-negative design and draw conclusions.
TEMPORAL CONFOUNDING
Assumptions and notation
Individuals in the population are infected by the target pathogen with time-varying hazard rate 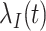 at time
at time 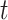 with cumulative hazard function
with cumulative hazard function 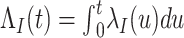 , where
, where 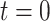 corresponds to the start of the study. We assume that everyone is susceptible at
corresponds to the start of the study. We assume that everyone is susceptible at 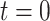 , although we later relax this assumption. Given infection with the target pathogen, the probability of developing symptomatic disease is
, although we later relax this assumption. Given infection with the target pathogen, the probability of developing symptomatic disease is 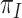 . We assume that infection confers immunity to the target disease, so the individual is not at risk for repeat infection during the remainder of the study.
. We assume that infection confers immunity to the target disease, so the individual is not at risk for repeat infection during the remainder of the study.
Individuals in the population are infected with nontarget pathogens causing the same clinical syndrome with time-varying intensity rate 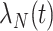 with cumulative intensity function
with cumulative intensity function 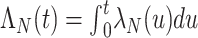 . Given infection with a nontarget pathogen, the probability of developing symptomatic disease is
. Given infection with a nontarget pathogen, the probability of developing symptomatic disease is  . Because we assume that there are several different causes of the clinical syndrome cocirculating, infection with a nontarget pathogen does not confer immunity. After each nontarget infection, that individual might be infected with another nontarget pathogen, following the same intensity function. Similarly, infection with the target disease does not confer immunity to the nontarget diseases.
. Because we assume that there are several different causes of the clinical syndrome cocirculating, infection with a nontarget pathogen does not confer immunity. After each nontarget infection, that individual might be infected with another nontarget pathogen, following the same intensity function. Similarly, infection with the target disease does not confer immunity to the nontarget diseases.
Each individual  in the population of size
in the population of size 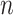 has vaccination time
has vaccination time 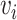 . We define a cumulative distribution for vaccination in the population
. We define a cumulative distribution for vaccination in the population 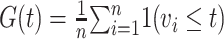 where
where 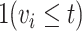 is an indicator of vaccination by time
is an indicator of vaccination by time 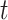 .
. 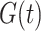 is the proportion of the population vaccinated by time
is the proportion of the population vaccinated by time 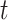 and has associated density/mass function
and has associated density/mass function 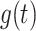 . We assume that vaccine confers an all-or-none vaccine effect to vaccinated individuals (13, 14). A proportion
. We assume that vaccine confers an all-or-none vaccine effect to vaccinated individuals (13, 14). A proportion 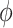 are fully protected by the vaccine, and the remaining
are fully protected by the vaccine, and the remaining 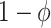 are unprotected. Vaccine effectiveness is
are unprotected. Vaccine effectiveness is 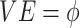 . We assume that the vaccine is immediately protective with no induction period. We further assume no waning of VE over time. We also assume that vaccine does not alter the probability of a clinical syndrome given infection
. We assume that the vaccine is immediately protective with no induction period. We further assume no waning of VE over time. We also assume that vaccine does not alter the probability of a clinical syndrome given infection  .
.
To reflect potential confounding by health-care seeking behavior, we allow the probability of seeking care given symptomatic disease to vary by vaccination status. Once symptoms appear, vaccinated and unvaccinated individuals are tested with probability 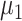 and
and 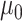 , respectively.
, respectively.
Consistent with other examinations of the test-negative design (4, 12), we assume the study uses inclusive sampling (13), also referred to as modified case-cohort sampling (19). Individuals are not censored even after they are known to have tested positive for the target pathogen. Under an inclusive sampling strategy, the odds ratio directly estimates the relative risk (13).
Expected cell counts and odds ratio
Test-negative design data is typically summarized in a 2 × 2 table (test positive/negative vs. vaccinated/unvaccinated at time of testing). We derive the expected cell counts at time 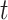 for unvaccinated test-positive cases
for unvaccinated test-positive cases 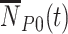 , vaccinated test-positive cases
, vaccinated test-positive cases 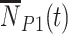 , unvaccinated test-negative controls
, unvaccinated test-negative controls 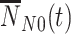 , and vaccinated test-negative controls
, and vaccinated test-negative controls 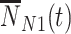 .
.
The expected (cumulative) cell counts between time 0 and time 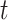 under a generic vaccination strategy with generic test-positive and test-negative rates are:
under a generic vaccination strategy with generic test-positive and test-negative rates are:
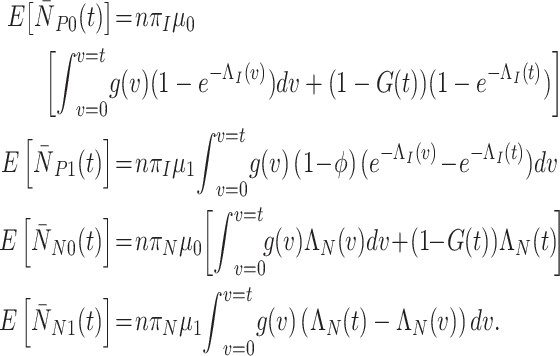 |
(1) |
The expressions for 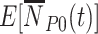 and
and 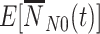 integrate over all vaccination times before
integrate over all vaccination times before  , considering events occurring between time 0 and vaccination; this is added to events that occur in individuals who have not yet been (or never will be) vaccinated. The expressions for
, considering events occurring between time 0 and vaccination; this is added to events that occur in individuals who have not yet been (or never will be) vaccinated. The expressions for 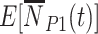 and
and 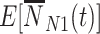 integrate over all vaccination times before
integrate over all vaccination times before 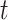 , considering events occurring between vaccination and time
, considering events occurring between vaccination and time 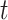 .
.
The expected changes in cell counts at time 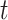 in some small interval
in some small interval 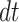 are:
are:
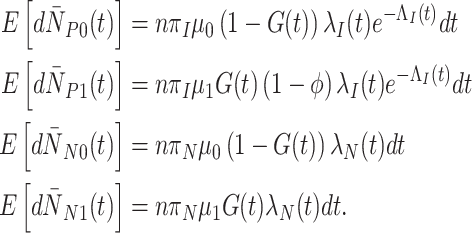 |
(2) |
We consider two test-negative design odds ratios. The first is the time-unadjusted (cumulative) test-negative design odds ratio through time 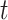 ,
, 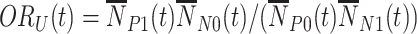 , that, following a first-order Taylor series expansion of the ratio and independence of the test-positive cases and test-negative controls, has expected value approximated by:
, that, following a first-order Taylor series expansion of the ratio and independence of the test-positive cases and test-negative controls, has expected value approximated by: 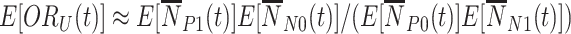 . The second is the time-adjusted test-negative design odds ratio at time
. The second is the time-adjusted test-negative design odds ratio at time 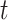 ,
, 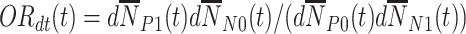 . To achieve this in practice, we stratify finely on time.
. To achieve this in practice, we stratify finely on time.
Varying vaccine coverage
When vaccination is completed before the start of the study with coverage 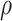 , the expected cell counts are:
, the expected cell counts are:
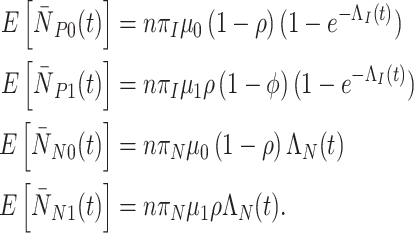 |
(3) |
From equation set (3), it follows that 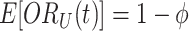 for all time
for all time 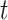 . Thus, calendar time is not a confounder.
. Thus, calendar time is not a confounder.
In contrast, under a generic vaccine rollout strategy, we see from equation set (1) that the time-unadjusted test-negative design odds ratio does not in general simplify to 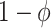 . For the time-adjusted test-negative design odds ratio, though,
. For the time-adjusted test-negative design odds ratio, though, 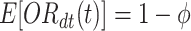 for all time
for all time 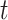 (see equation set (2)). Thus, we confirm the importance of adjusting for calendar time when vaccine is rolled out during the study.
(see equation set (2)). Thus, we confirm the importance of adjusting for calendar time when vaccine is rolled out during the study.
If vaccination is completed early on in the study, one option is to restrict analysis to the period after all vaccine has been provided. We demonstrate in Web Appendix 1 (available at https://doi.org/10.1093/aje/kwaa084) that the time-unadjusted test-negative design odds ratio is consistent for the true vaccine effect in this case. In practice, the benefit of not having to adjust for calendar time should be weighed against potential information lost by excluding early data.
These results suggest that a natural approach to adjust for calendar time, instead of finely stratifying, is to break up the study period into windows in which vaccination coverage is relatively constant. We could visually examine the proportion vaccinated over time in the test negatives to identify breaks (see Figure 4b in Bond et al. (17) for an example). Within each time window, there will be no (or minimal) temporal confounding.
For generic vaccine roll-out but constant rates 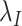 and
and 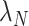 , expected cell counts are:
, expected cell counts are:
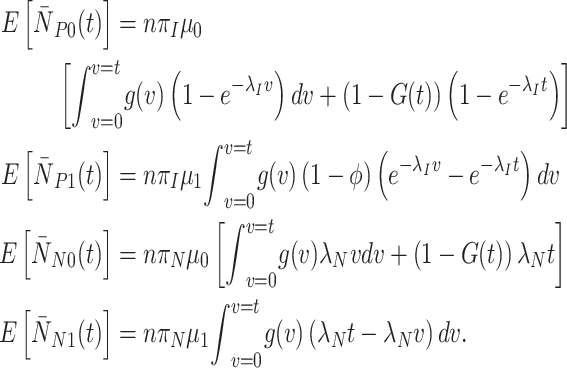 |
(4) |
Even though there is no association between time and hazard rate, the time-unadjusted test-negative design odds ratio does not simplify to 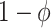 because test-positive cases come from the depleted at-risk population (
because test-positive cases come from the depleted at-risk population (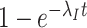 terms), but test-negative controls come from the conserved source population (
terms), but test-negative controls come from the conserved source population (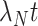 terms). Nonetheless, when the disease is rare, the time-unadjusted odds ratio simplifies following a first-order Taylor series approximation (
terms). Nonetheless, when the disease is rare, the time-unadjusted odds ratio simplifies following a first-order Taylor series approximation (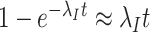 ); thus, temporal confounding is minimal.
); thus, temporal confounding is minimal.
We demonstrate the existence of a theoretical (though unrealistic) test-positive hazard rate that eliminates temporal confounding; this is described in Web Appendix 1.
Out-of-season controls
We use our results to address open questions about out-of-season controls. Jackson and Nelson (1) describe including these controls as inducing immortal person-time bias, but this implies that data are analyzed as a cohort. In fact, the test-negative controls serve as a proxy for characterizing vaccine coverage in the underlying source population. Table 1 demonstrates this concept heuristically.
Table 1.
Sample Test-Negative Design Tablea
| Overall | Test-Positive Cases | Test-Negative Controls (In Season) | Test-Negative Controls (Out of Season) | Source Population |
|---|---|---|---|---|
| Vaccinated | a | c | e |
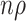
|
| Unvaccinated | b | d | f |
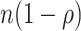
|
a Sample test-negative design table for a population of size n with constant vaccination coverage 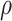 (all vaccinations completed before the beginning of the study). Hypothetical case counts for each combination of vaccination status and test status/timing are denoted by a through f.
(all vaccinations completed before the beginning of the study). Hypothetical case counts for each combination of vaccination status and test status/timing are denoted by a through f.
As long as the test-negative controls are representative of the underlying health-care-seeking source population (given the central assumption that vaccine does not influence the intensity rate of test-negative disease), the time-unadjusted odds ratio (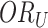 ) estimates the relative risk (RR) because
) estimates the relative risk (RR) because 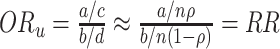 . Thus, where vaccination coverage does not vary in and out of season
. Thus, where vaccination coverage does not vary in and out of season 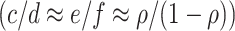 , out-of-season controls do not induce bias. Similarly, from equation set (3), when vaccination is completed before the study, the time-unadjusted test-negative design odds ratio is consistent even if the test-positive hazard function is very small or equal to zero at times, representing time out of season. Including out-of-season controls can enable more precisely estimation of vaccination coverage.
, out-of-season controls do not induce bias. Similarly, from equation set (3), when vaccination is completed before the study, the time-unadjusted test-negative design odds ratio is consistent even if the test-positive hazard function is very small or equal to zero at times, representing time out of season. Including out-of-season controls can enable more precisely estimation of vaccination coverage.
Where vaccination coverage varies over time, including out-of-season test-negative controls can induce bias in the time-unadjusted test-negative design odds ratio. Including controls before the season when coverage is lowest could bias VE downward. Including cases after the season when coverage is highest could bias VE upward. Including cases during intermittent weeks in the season with no cases would seem to induce the smallest bias.
Nonetheless, we previously demonstrated the importance of adjusting for calendar time when vaccination coverage is varying over time. If this is done using a conditional logistic regression model, for example, time periods with no cases will drop out of the conditional likelihood. Consistent with simulation results (17), there is no further advantage to restricting the analysis period after adjusting for time.
In summary, the more important analytical decision is whether to adjust for time. Whether or not time is adjusted for, there is no apparent harm in including out-of-season controls unless they differ with respect to other key confounders. Either these controls add precision to a time-unadjusted analysis or are uninformative in a time-adjusted analysis.
Open population
Finally, we consider open populations in which cohorts enter over time. We demonstrate these concepts using a series of simple examples with 2 cohorts, although the logic quickly extends to any finite number of cohorts. The first cohort enters at 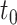 , and the second cohort enters at
, and the second cohort enters at 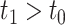 .
.
For the first setting, we assume that vaccination is completed prior to recruitment in both cohorts. For example, infants are eligible to be included in the study once they have reached an age when they would have completed all doses, and infants either receive the vaccine on time or not at all. Vaccine coverage is 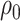 in the first cohort and
in the first cohort and 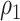 in the second cohort.
in the second cohort.
When 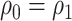 (vaccination coverage is constant across cohorts), the time-unadjusted test-negative design odds ratio is consistent for the true vaccine effect (see Web Appendix 2). This is true when there are more than 2 cohorts, as long as they all have equal vaccination coverage. Although cohort is associated with the probability of testing positive (given that older cohorts have greater immunity), cohort is not a confounder because vaccine coverage is constant across cohorts. Calendar time is also not a confounder because vaccine coverage is fixed over time.
(vaccination coverage is constant across cohorts), the time-unadjusted test-negative design odds ratio is consistent for the true vaccine effect (see Web Appendix 2). This is true when there are more than 2 cohorts, as long as they all have equal vaccination coverage. Although cohort is associated with the probability of testing positive (given that older cohorts have greater immunity), cohort is not a confounder because vaccine coverage is constant across cohorts. Calendar time is also not a confounder because vaccine coverage is fixed over time.
When 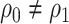 (vaccination coverage varies across cohorts), cohort is an important confounder. When we adjust for cohort, we see that that the odds ratio is unbiased (see Web Appendix 2). It is not necessary to adjust for calendar time after adjusting for cohort because vaccination status does not change over time within cohort.
(vaccination coverage varies across cohorts), cohort is an important confounder. When we adjust for cohort, we see that that the odds ratio is unbiased (see Web Appendix 2). It is not necessary to adjust for calendar time after adjusting for cohort because vaccination status does not change over time within cohort.
Alternatively, imagine a disease that has been endemic in the population such that immunity has built up especially in older cohorts. A vaccine is made available and is deployed over time during an outbreak. If vaccination is rolled out over time to all populations uniformly, then calendar time is a confounder, but cohort is not because at any time coverage is equal across cohorts. If the vaccine is rolled out differentially across cohorts, though, say to preferentially target children, then both cohort and calendar times will be confounders (see Web Appendix 2). Thus, to determine whether cohort is a confounder, it is important to examine whether vaccination coverage varies across cohorts in the source population.
APPLYING OUR FINDINGS
We consider 3 studies applying the test-negative design, and we discuss how our findings inform their results or approach.
Cholera trial
Ali et al. (20) used a test-negative design to reanalyze data from 2 cluster-randomized cholera vaccine trials and a nonrandomized study. For our example, we consider the trial in Kolkata, India, although the implications are the same across studies. The trial enrolled residents at least 1 year of age (21). Two doses of vaccine or placebo were provided in 2 rounds, each lasting no more than 3 weeks. Follow-up began 14 days after the second dose of vaccine. The authors used the first episode of noncholera diarrhea for each participant as a test-negative control. Their primary model adjusted for age at vaccination and severity, and a secondary model also adjusted for seasonality but found no change in the results. Overall, the test-negative design estimate of VE was highly concordant with the cohort estimate from the original trial.
Calendar time would not be a confounder because vaccination was essentially completed before follow-up began. Vaccine coverage was also stable across age groups because of randomization (always 50%), so it might not be necessary to adjust for age. In fact, the authors showed that adjusting for age at first dose and severity had virtually no impact on estimated VE (Table 1 in Ali et al. (20)).
Rotavirus trials
Schwartz et al. (22) used a test-negative design to reanalyze data from 3 individually-randomized rotavirus vaccine trials. All trials enrolled infants aged approximately 4–12 weeks during a 2-year study period, and they were then randomized to vaccine or placebo and followed longitudinally. The authors defined a trial participant as a test-negative control if they experienced at least 1 severe rotavirus-negative diarrheal episode and had no severe rotavirus-positive episodes. They found high concordance between the unadjusted test-negative design and trial estimates with one notable exception. In the analysis of a trial in Ghana, Kenya, and Mali, the authors showed that restricting to the rotavirus season in Ghana and Mali (but using year-round data in Kenya) was important for reducing bias in the test-negative design.
We would not expect confounding by calendar time or by age cohort because vaccination was completed before follow-up. Furthermore, coverage is 50% in the trial population at all times and in all age cohorts due to randomization. We see concordance in trials in countries that also have seasonal patterns of transmission (e.g., South Africa, Malawi, Bangladesh). In Ghana and Mali, vaccination coverage is overestimated in test-negative controls (>50%), particularly in year 2. Restricting to the rotavirus season reduces this imbalance, but it reduces the number of test-negative controls from 373 to 139. A possible explanation for this imbalance is that controls are participants known to have never tested positive (exclusive instead of inclusive sampling). If vaccine is protective, more controls from the unvaccinated arm are removed, thereby overrepresenting vaccine coverage in controls, especially in high-incidence countries.
Dengue trial
Anders et al. (19) introduced the concept of cluster-randomized test-negative design trials motivated by community-level dengue interventions. The data are analyzed by intention-to-treat, where exposure to the intervention is not time-varying. Thus, adjustment for calendar time is not required. The authors note the importance of recruiting test-negative controls only when test-positive illness is circulating, citing Jackson and Nelson (1).
We counter that restricting to time in-season might not be necessary for a cluster-randomized test-negative design trial. Unless there are large changes in migration that are differential across the study arms, the proportion exposed should be constant over time. Including test-negative controls out of season would likely improve precision and power without inducing bias.
DISCUSSION
We undertook a theoretical examination of temporal confounding in the test-negative design, focusing on time-varying exposure, out-of-season controls, and open populations. Our results confirm that temporal confounding occurs when vaccine coverage changes during the study, even with constant test-positive and test-negative hazard rates. Nonetheless, this bias is minimal for rare diseases. We show that including out-of-season controls does not induce bias unless vaccine coverage is different in versus out of season. If calendar time is adjusted for, these controls will be largely uninformative. Where coverage is stable, including out-of-season controls can improve precision. Finally, we described settings in open populations where age cohort (i.e., time in the population) might be a confounder.
We made several simplifying assumptions. We do not consider changes in reporting over time, interference between test-positive and test-negative pathogens due to temporary innate immunity, severity as a confounder, and other key risk factors for infection, such as age or high-risk status. These generalizations should be studied in future work. We assumed no differential loss to follow-up in the population. For severe diseases, such as Ebola virus, differential survival in the vaccinated and unvaccinated groups is expected to lead to bias (23), although this bias will likely be small where the cumulative incidence is low. Our analysis also assumes an all-or-none vaccine. Previous work has demonstrated that inclusive sampling with a leaky vaccine (vaccine confers partial protection) yields biased estimators (12). Further study is needed on the test-negative design and leaky vaccines; where feasible, innovations to allow us to censor individuals who have been previously infected could reduce bias (13, 24, 25).
The test-negative design is rapidly growing in popularity and has many potential future applications. It is highly cost-effective and can be used where a placebo-controlled randomized trial is not practical or ethical. The design will be especially useful for postlicensure surveillance and bridging studies, to evaluate new vaccine formulations, VE in new populations, or effectiveness against new strains. There are also interesting opportunities to integrate test-negative designs with cluster randomized trials (19).
The test-negative design is being applied in diverse settings, and the need for theoretical examination of its properties is clear. We contribute to understanding the critical role of temporal confounding in test-negative designs.
Supplementary Material
Acknowledgments
Author affiliations: Department of Biostatistics, University of Florida, Gainesville, Florida (Natalie E. Dean, Ira M. Longini, Jr.); Vaccine and Infectious Disease Division, Fred Hutchinson Cancer Research Center, Seattle, Washington (M. Elizabeth Halloran); and Department of Biostatistics, University of Washington, Seattle, Washington (M. Elizabeth Halloran).
This research was supported by the National Institute of Allergy and Infectious Diseases (grant R01 AI139761).
Conflict of interest: none declared.
References
- 1. Jackson ML, Nelson JC. The test-negative design for estimating influenza vaccine effectiveness. Vaccine. 2013;31(17):2165–2168. [DOI] [PubMed] [Google Scholar]
- 2. De Serres G, Skowronski DM, Wu XW, et al. The test-negative design: validity, accuracy and precision of vaccine efficacy estimates compared to the gold standard of randomised placebo-controlled clinical trials. Euro Surveill. 2013;18(37):20585. [DOI] [PubMed] [Google Scholar]
- 3. Broome CV, Facklam RR, Fraser DW. Pneumococcal disease after pneumococcal vaccination—an alternative method to estimate the efficacy of pneumococcal vaccine. N Engl J Med. 1980;303(10):549–552. [DOI] [PubMed] [Google Scholar]
- 4. Foppa IM, Ferdinands JM, Chaves SS, et al. The case test-negative design for studies of the effectiveness of influenza vaccine in inpatient settings. Int J Epidemiol. 2016;45(6):2052–2059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Sullivan SG, Tchetgen Tchetgen EJ, Cowling BJ. Theoretical basis of the test-negative study design for assessment of influenza vaccine effectiveness. Am J Epidemiol. 2016;184(5):345–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Westreich D, Hudgens MG. Invited commentary: beware the test-negative design. Am J Epidemiol. 2016;184(5):354–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Sullivan SG, Feng S, Cowling BJ. Potential of the test-negative design for measuring influenza vaccine effectiveness: a systematic review. Expert Rev Vaccines. 2014;13(12):1571–1591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Franke MF, Jerome JG, Matias WR, et al. Comparison of two control groups for estimation of oral cholera vaccine effectiveness using a case-control study design. Vaccine. 2017;35(43):5819–5827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Azman AS, Parker LA, Rumunu J, et al. Effectiveness of one dose of oral cholera vaccine in response to an outbreak: a case-cohort study. Lancet Glob Health. 2016;4(11):e856–e863. [DOI] [PubMed] [Google Scholar]
- 10. Tate JE, Patel MM, Cortese MM, et al. Use of patients with diarrhea who test negative for rotavirus as controls to estimate rotavirus vaccine effectiveness through case-control studies. Clin Infect Dis. 2016;62(suppl 2):S106–S114. [DOI] [PubMed] [Google Scholar]
- 11. Foppa IM, Haber M, Ferdinands JM, et al. The case test-negative design for studies of the effectiveness of influenza vaccine. Vaccine. 2013;31(30):3104–3109. [DOI] [PubMed] [Google Scholar]
- 12. Lewnard JA, Tedijanto C, Cowling BJ, et al. Measurement of vaccine direct effects under the test-negative design. Am J Epidemiol. 2018;187(12):2686–2697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Smith PG, Rodrigues LC, Fine PEM. Assessment of the protective efficacy of vaccines against common diseases using case-control and cohort studies. Int J Epidemiol. 1984;13(1):87–93. [DOI] [PubMed] [Google Scholar]
- 14. Halloran ME, Longini IM Jr, Struchiner CJ. Design and Analysis of Vaccine Studies. New York, NY: Springer; 2010. [Google Scholar]
- 15. Jacoby P, Kelly H. Is it necessary to adjust for calendar time in a test negative design?: responding to: Jackson ML, Nelson JC. The test negative design for estimating influenza vaccine effectiveness. Vaccine 2013;31(April (17)):2165–8. Vaccine. 2014;32(25):2942. [DOI] [PubMed] [Google Scholar]
- 16. Griffin MR, Monto AS, Belongia EA, et al. Effectiveness of non-adjuvanted pandemic influenza a vaccines for preventing pandemic influenza acute respiratory illness visits in 4 U.S. communities. PLoS One. 2011;6(8):4–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Bond HS, Sullivan SG, Cowling BJ. Regression approaches in the test-negative study design for assessment of influenza vaccine effectiveness. Epidemiol Infect. 2016;144(8):1601–1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Sullivan SG, Laine E, Kelly H. Variable definitions of the influenza season and their impact on vaccine effectiveness estimates. Vaccine. 2013;31(40):4280–4283. [DOI] [PubMed] [Google Scholar]
- 19. Anders KL, Cutcher Z, Kleinschmidt I, et al. Cluster-randomized test-negative design trials: a novel and efficient method to assess the efficacy of community-level dengue interventions. Am J Epidemiol. 2018;187(9):2021–2028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Ali M, You YA, Sur D, et al. Validity of the estimates of oral cholera vaccine effectiveness derived from the test-negative design. Vaccine. 2016;34(4):479–485. [DOI] [PubMed] [Google Scholar]
- 21. Sur D, Lopez AL, Kanungo S, et al. Efficacy and safety of a modified killed-whole-cell oral cholera vaccine in India: an interim analysis of a cluster-randomised, double-blind, placebo-controlled trial. Lancet. 2009;374(9702):1694–1702. [DOI] [PubMed] [Google Scholar]
- 22. Schwartz LM, Halloran ME, Rowhani-Rahbar A, et al. Rotavirus vaccine effectiveness in low-income settings: an evaluation of the test-negative design. Vaccine. 2017;35(1):184–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Flanders WD, Dersimonian R. Estimation of risk ratios in case-based studies with competing risks. Stat Med. 1990;9(4):423–435. [DOI] [PubMed] [Google Scholar]
- 24. Dean NE. RE: “Measurement of vaccine direct effects under the test-negative design”. Am J Epidemiol. 2019;188(4):806–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Lewnard JA, Tedijanto C, Cowling BJ, et al. The authors reply. Am J Epidemiol. 2019;188(4):807–808. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


