Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jul 24;20(9):6412–6419. doi: 10.1021/acs.nanolett.0c01963

A New Signature for Strong Light–Matter Coupling Using Spectroscopic Ellipsometry

Philip A Thomas 1,*, Wai Jue Tan 1, Henry A Fernandez 1, William L Barnes 1
PMCID: PMC7608940  PMID: 32709208

Abstract

graphic file with name nl0c01963_0006.jpg

Light–matter interactions can occur when an ensemble of molecular resonators is placed in a confined electromagnetic field. In the strong coupling regime the rapid exchange of energy between the molecules and the electromagnetic field results in the emergence of hybrid light–matter states called polaritons. Multiple criteria exist to define the strong coupling regime, usually by comparing the splitting of the polariton bands with the line widths of the uncoupled modes. Here, we highlight the limitations of these criteria and study strong coupling using spectroscopic ellipsometry, a commonly used optical characterization technique. We identify a new signature of strong coupling in ellipsometric phase spectra. The combination of ellipsometric amplitude and phase spectra yields a distinct topological feature that we suggest could serve as a new criterion for strong coupling. Our results introduce the idea of ellipsometric topology and could provide further insight into the transition from the weak to strong coupling regime.

Keywords: strong coupling, ellipsometry, polaritons, optical microcavities, optical phase response, Rabi splitting

1. Introduction

Light–matter interactions can occur when an ensemble of molecular resonators is placed in a confined electromagnetic field. If the field and resonators have similar excitation energies and the coupling strength between them exceeds the mean of their decay rates, the energy levels of the confined field mode and the resonator can be modified, i.e., they are strongly coupled.1,2 The characteristic feature of strong coupling is the formation of two hybrid states known as the upper and lower polariton bands.3 Confined electromagnetic fields can be generated by optical microcavities4−6 or surface plasmons;7,8 resonances can be provided by organic molecules.5−10 The potential of strong coupling to control light–matter interactions is far ranging, with applications identified in the areas of quantum information,11,12 polaritonic chemistry,13 and lasing,14 among others.

Strongly coupled systems are usually characterized by an intensity measurement (such as reflectivity,5 extinction,8 transmission,6 or luminescence7) which is used to create a dispersion plot (energy versus incident angle of light θ or wavevector Inline graphic, where λ is wavelength of incident light; see Figure 1a for an example). The signature of strong coupling observed in these plots is an anticrossing of the confined electromagnetic mode and the material resonance. The Rabi splitting, Ω, is the minimum energy difference between the two modes. Multiple criteria for strong coupling exist and are usually defined by comparing the line widths of the uncoupled resonances with Ω.2 These criteria predict the transition from weak to strong coupling at very different values of Ω.

Figure 1.

Figure 1

Open in a new tab

Strong coupling between optical microcavity mode and organic molecules. (a) Typical dispersion plot of an optical cavity mode coupled to organic molecules (here, merocyanine). Data plotted for negative k// were calculated using transfer matrix method (merocyanin was modeled using a Lorentz oscillator). Data plotted for positive k// were obtained using Fourier transmission spectroscopy (Figure S1). Experimental transmission values have been scaled up by 50% to match calculated data, compensating for a drop in intensity due to scattering. The green and orange lines indicate the positions of the uncoupled cavity and molecular resonances, respectively; the purple lines show the calculated positions of the upper and lower polariton bands. (b) Sample design for strong coupling experiment showing a dye-doped polymer matrix between two silver mirrors.

The combined study of the amplitude and phase response of an optical system can provide insight that is not possible from intensity measurements alone. By analyzing the amplitude and phase response of plasmon antenna array etalons, Berkhout and Koenderink15 showed that points of perfect absorption in such structures are topologically protected. Kravets et al.16 showed that the phase response of plasmonic nanostructures around points of perfect absorption can be used in single molecule detection. To the best of our knowledge no experiments have studied the phase response in molecular strong coupling.

In this work we use spectroscopic ellipsometry to study the combined amplitude and phase response of strongly coupled resonances. We characterize the strong coupling of optical microcavities with organic molecules and that of surface lattice resonances with waveguide modes. We observe the transition from weak to strong coupling using the ellipsometric phase shift and identify a candidate signature of strong coupling. Combining amplitude and phase data shows that the optical response of the system undergoes a change in topology during the transition from weak to strong coupling. We compare this transition point with the existing criteria for strong coupling. Our results suggest a new criterion for strong coupling, free of the limitations of existing strong coupling criteria, and reveal a new way to study the topology of optical systems.

2. Results

We studied strong coupling between organic molecular resonances and optical cavity modes (see the Supporting Information for fabrication details). The microcavity design is illustrated in Figure 1b; it consisted of two silver mirrors (each of thickness 30 nm) separated by a PMMA (poly(methyl methacrylate)) dielectric spacer layer (thickness 150 nm). Embedded in the PMMA layer are spyropyran (SPI) molecules (1′,3′-dihydro-1′,3′,3′-trimethyl-6-nitrospiro[2H-1-benzopyran-2, 2′-(2H)-indole]). SPI is a transparent photochromic molecule; after exposure to ultraviolet radiation it undergoes photoisomerisation and is converted to merocyanine (MC)17 with an optical transition at 2.2 eV (Figure S2). The cavity thickness was chosen so that the first-order cavity resonance occurred at 2.2 eV for light incident at θ = 60°. Exposing the cavity to ultraviolet radiation converts SPI to MC and the first-order cavity mode couples to the molecular resonance of MC. This allows for observation of the transition from weak to strong coupling.6

All samples were characterized using spectroscopic ellipsometry (Figure 2a), which measures the complex reflection ratio ρ in terms of the parameters Ψ and Δ:

2. 1

where rp and rs are the Fresnel reflection (amplitude) coefficients for p- and s-polarized light, respectively, and tan(Ψ) is the amplitude of ρ and provides the ratio of rp and rs; Δ is the difference in the phase shifts undergone by p- and s-polarized light upon reflection (further details in the Supporting Information). The dominant use of spectroscopic ellipsometry is in determining the thickness and optical constants of thin films.18,19

Figure 2.

Figure 2

Open in a new tab

Transition from weak-to-strong coupling regime observed with intensity and phase measurements. (a) Schematic of spectroscopic ellipsometer. θ = 60° for all measurements. (b) The plot for tan(Ψ) and Δ for a series of uncoupled cavity modes in a ∼2 μm-thick PMMA microcavity. (c, d) Initial (blue) and final (orange) measurements of SPI/MC microcavity made with (c) Rp and (d) tan(Ψ) (top) and Δ (bottom) measurements showing the change from a single uncoupled cavity mode to strongly coupled MC/cavity modes. The transition from weak-to-strong coupling as a function of time is shown with Rp data in (e) and with cos(Δ) data in panel (f). The dashed blue and orange lines show the positions in time from which the data in (c) and (d) were taken.

The ellipsometric response of a multimode Ag/PMMA/Ag microcavity (thickness ∼2 μm) at θ = 60° is shown in Figure 2b. Since these measurements were made at an oblique incident angle, the cavity resonances occur at different energies for p- and s-polarized light. In tan(Ψ), a resonance occurs when rp < rs (tan(Ψ) < 1) and also when rs < rp (tan(Ψ) > 1). Δ is the difference between the phase change experienced by p- and s-polarized light; a cavity resonance will cause a characteristic modulation in Δ.

We exposed the SPI microcavity to UV irradiation and measured the change in ρ (Figure 3) and its derived values (Rp = |rp|2, tan(Ψ) and Δ (Figure 2), as SPI underwent conversion to MC. All measurements were taken at θ = 60°.

Figure 3.

Figure 3

Open in a new tab

Evolution of ρ through transition from weak-to-strong coupling. All measurements made at θ = 60°. (a–c) The measured ellipsometric parameters tan(Ψ), Δ, and ρ, respectively, for the SPI/MC microcavity at the times t = 10 s (blue curve), t = 220 s (orange curve), t = 550 s (green curve), and t = 2000 s (purple curve). The critical region of interest in (c) is indicated by the dashed gray box. The point with maximum tan(Ψ) between the two polariton minima in the final (purple) data set is indicated by the red arrows.

Figure 2c shows the Rp spectrum before and after the SPI microcavity was exposed to ultraviolet radiation. The MC resonance at 2.21 eV couples to the cavity mode at 2.24 eV; the maximum Rabi splitting observed was (574 ± 103) meV.

Figure 2e shows the time evolution of Rp spectra of the microcavity as SPI is converted to MC. The high time resolution of our measurements (one scan every 11 s over a total acquisition time of 45 min) demonstrates a clear transition of the reflection spectrum from an uncoupled to a coupled state. After the first hundred seconds of ultraviolet exposure the cavity resonance splits into two and the rate of splitting slows down exponentially. As Ω is directly proportional to 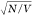Inline graphic, where N is the number of MC molecules in the cavity and V is the cavity volume;2 this implies that the conversion of SPI to MC molecules follows an exponential relationship with time.

We plot Δ in Figures 2d (initial and final state) and 2f (change with time; cos(Δ) has been plotted to improve contrast). In Figure 2c (Rp) the upper and lower polariton bands are, like the original cavity mode, approximately Lorentzian in form. In contrast, the phase signatures of the upper and lower polariton bands in Figure 2d and f have different forms, as if a point of inflection has been added to the center of the original phase response. This differs from the phase response of the multimode cavity in Figure 2b which shows closely spaced but uncoupled cavity modes. Since the MC molecular resonance does not change with θ and is not polarization dependent, the splitting of the asymmetric Δ response of the microcavity shows that the properties of the original cavity mode have been inherited by the upper and lower polariton bands. This suggests that phase measurements can distinguish between coupled resonances and uncoupled but closely spaced resonances in a way which is not possible using intensity measurements.

The parameters tan(Ψ) and Δ are plotted in Figures 3a and b. Four data sets are plotted in these figures, i.e., the initial SPI microcavity (blue lines, t = 10 s); an intermediate point where some SPI has been converted to MC but not sufficiently for strong coupling (orange lines, t = 220 s); a point at which the resonance is split in both tan(Ψ) and Δ (green lines, t = 550 s); and the final strongly coupled MC microcavity (purple lines, t = 2000 s). These data sets are used to plot ρ in the complex plane as a function of energy (from 1.1–3.5 eV) in Figure 3c. For a simple silver surface (Figure S3a, b), ρ traces out an arc from E = 1.5 eV, ρ ≈ −0.8 + 0.55i, to E = 3.5 eV, ρ ≈ −0.1 + 0.85i. This arc, present in all curves in Figure 3c, results from the optical response of Ag as it changes from a mirror-like response at lower energies (perfect reflection occurs at ρ = −1) toward interband transitions at around 3.9 eV.20

The changes in both tan(Ψ) and Δ associated with a cavity resonance observed at θ ≠ 0 combine to add a loop that breaks the Ag arc in ρ. This loop, representing the first-order microcavity resonance, appears along the Ag arc at ρ ≈ −0.65 + 0.75i (see Figure S3c, d).

As SPI is converted into MC the area enclosed by the cavity resonance in ρ reduces, corresponding to a decrease in the strength of the cavity resonance. As MC is created a “kink” appears at ρ ≈ −0.40 + 0.55i and grows on the side of the cavity loop (orange curves). Figure 3a shows this is a change from a single resonance to two resonances that are not yet fully distinct. Between the orange and green curves two resonances become observable in tan(Ψ) and the point of inflection in Δ evolves into the local minimum observed in Figure 2d, f. In Figure 3c this corresponds to the dimple evolving into a secondary loop inside the original resonance loop (a change in ellipsometric topology). The point of maximum tan(Ψ) between the two polariton minima in the final data set is indicated by red arrows, showing that here the secondary loop lies between the positions of the two polaritons on the primary loop. In contrast, plotting uncoupled resonances in ρ gives one independent loop per uncoupled resonance. These loops can overlap but do not form secondary loops (see ρ plotted for a multimode cavity in Figure S3e, f).

Secondary loops in ρ are not unique to MC microcavities. Figures 4a–c show strong coupling between an optical microcavity mode and the excitonic resonance (2.1 eV) in the J-aggregate TDBC21 (see Figure 4a for sample design and the Supporting Information for fabrication details). Figure 4b shows a splitting of the phase response of the initial cavity mode. Figure 4c shows a secondary loop in ρ, similar to the one shown in Figure 3c.

Figure 4.

Figure 4

Open in a new tab

Signature of strong coupling in ρ for other systems. Plots of tan(Ψ)/Δ and ρ for strong coupling in (a–c) a TDBC microcavity and (d–f) a hybrid surface lattice resonance/waveguide structure, where both feature the same secondary loop observed in Figure 3. θ = 60° for all measurements. (a) Schematic of the TDBC microcavity measured in (b) and (c). (d) Schematic of the hybrid surface lattice resonance/waveguide structure measured in (e) and (f), where a = 1550 nm, w = 450 nm, h1 = 75 nm, and h2 = 65 nm. The points corresponding to the maximum value of tan(Ψ) between the two polariton minima are indicated by red arrows.

Figures 4d–f show strong coupling between plasmonic surface lattice resonances and optical waveguide modes. The structure (Figure 4d) is a one-dimensional gold grating (period 1.55 μm, grating element width 450 nm and height 70 nm) on a 65 nm thick gold sublayer all covered by a 400 nm thick layer of hafnium(IV) oxide (see the Supporting Information for fabrication details). The grating structure supports plasmonic surface lattice resonances and the hafnium(IV) oxide layer supports guided modes which can become strongly coupled to the plasmonic surface lattice resonance at around 0.8 eV.22 The parameter ρ for such a system is plotted in Figure 4f, which also shows a secondary loop. The secondary loop varies in size as the incident angle changes (see Figure S4). The innermost points of the secondary loops and their associated values of tan(Ψ) and Δ are indicated by red arrows. In the SPI/MC microcavity (Figure 3), where the polariton bands have roughly equal amplitude, the innermost point of the secondary loop corresponded to a point between the two polariton bands. For the TDBC/cavity and SLR/waveguide (Figure 4), where the polariton bands have very different amplitudes, the innermost points of both secondary loops correspond to the minima of the weaker polariton band.

3. Discussion

The existing criteria for strong coupling depend variously on the coupling strength g, the Rabi splitting Ω, the losses of the confined mode of the electric field and molecular resonator (γc and γm, respectively), and the energy of the uncoupled cavity mode and molecular excitation Ec,m (for strong coupling Ec ≈ Em ≡ E0). These criteria are summarized in Table 1 and are discussed in detail in the Supporting Information. Here, we apply these criteria to our results and compare them with the formation of the secondary loop in Figure 3.

Table 1. Criteria for Strong Coupling and Summary of Different Criteria for Strong Coupling Used in the Literaturea.

name criterion (theory) criterion (experiment)
Sparrow’s23 The spectral midpoint between two resonances shows a local minimum.
Savona et al.24 4g > |γc – γm| Ω > |Γc – Γm|
PT-symmetric Savona et al.24,25 4g > γc + γm Ω > Γc + Γm
ultrastrong coupling26 g/E0 > 0.1 Ω/E0 > 0.2
Open in a new tab
a

Notation: g is the coupling strength, Ω is the Rabi splitting, γc,m and Γc,m are the losses and fwhm of the confined electric field mode and molecular resonator, respectively, and E0 is the uncoupled transition energy of the electromagnetic cavity mode and the molecular resonance (which are assumed to be approximately equal). See the Supporting Information for a detailed discussion of each criterion.

While we cannot directly compare the coupling strength g with the losses γ, we can compare the experimentally measurable Rabi splitting Ω with the full-width at half-maxima (fwhm) of the uncoupled resonances of the cavity Γc and the MC molecular transition Γm. We modeled the SPI/MC microcavity using a Fresnel model (see the Supporting Information for details). The MC resonance was modeled using a single Lorentz oscillator:

3.

where ϵb is the background permittivity, f is a dimensionless strength, Bm ≈ Γc, and E0 the energy of the molecular resonance. The increase in MC molecules was modeled by increasing f. On average the calculated Ω differed from the experimentally observed Ω by 8%, which is a good level of agreement for such a simple model. In Figure 5 we plot Ω/E0 as a function of f. It is possible to measure Ω and fwhm’s in two ways: one is to use a fixed-θ spectrum (Figure 5a: this is how all data in Figures 2–4 were acquired) and the other is to use a fixed-k// spectrum (Figure 5b). We plot calculated fixed-θ Ω/E0 in Figure 5c and calculated fixed-k// Ω/E0 in Figure 5d.

Figure 5.

Figure 5

Open in a new tab

Comparison of different criteria for strong coupling. (a, b) Plots showing how fixed-angle (θ) and fixed-wavevector (k//) spectra are projected onto dispersion plots. (c, d) Plots showing how the calculated Rabi splitting from (c) fixed-θ (θ = 60°) and (d) fixed-wavevector (k// = 9.2 μm–1) spectra changes as a function of Lorentz oscillator amplitude. The shaded regions of these plots show where different strong coupling criteria are fulfilled.

The shaded regions in Figures 5c and 5d show the limits of the various strong coupling criteria described above: Sparrow’s criterion (gray), the Savona et al. criterion (red), the PT-symmetric Savona et al. criterion (green), and the ultrastrong coupling criterion (purple). We have also plotted the region (shaded blue) in which the secondary loop shown in Figure 3 appears. The differences between the two plots can be explained by the difference in Ω (and to a lesser extent by the difference in fwhm) measured in the two configurations.

The relationships between Ω/E0 and ln(f) in Figures 5c and 5d are described well by a linear-log plot. For Figure 5c:

3.

and for Figure 5d:

3.

In the fixed-θ case the scan line in Figure 5a intersects each polariton band at different k//, giving a larger Ω and a larger rate of splitting with increasing f. This explains why the fixed-θ gradient is 9% higher than the fixed-k// gradient and the 16% difference in the y-intercept between the two fits, which is almost identical to the increase in Ω when moving from fixed-k// to fixed-θ (on average 17%).

The higher values of Ω in fixed-θ plots affect the points at which the various criteria for strong coupling are satisfied. The ultrastrong coupling criterion depends solely on Ω/E0, so it requires a lower value of f to be fulfilled in fixed-θ plots. The Savona et al. and PT-symmetric criteria depend on Ω and Γc,m. As the change in Ω is much larger than the changes in Γc,m when moving from fixed-k// to fixed-θ, the Savona et al. and PT-symmetric criteria are also fulfilled at slightly lower f and Ω. The higher Ω value in the fixed-θ case is sufficiently large that the Savona et al. criterion is fulfilled at the same point as Sparrow’s criterion (that is, when two resonances are first resolved). Overall, these differences are relatively small, and the relative stringencies of the criterion are largely unchanged when moving from fixed-k// to fixed-θ spectra. A fixed-θ spectrum can thus provide a similar level of information to that obtained from a fixed-k// spectrum in the analysis of strong coupling experiments.

The most commonly used criterion (the PT-symmetric Savona et al. criterion) is much more stringent, in our case being comparable with the ultrastrong coupling criterion. The variant of this criterion used in experimental analysis2 (Ω > Γc + Γm) only approximately matches the originally derived criteria since it utilizes Ω and Γc,m, not g and γc,m. For this reason we suggest that the PT-symmetric Savona et al. criterion is consistently too conservative in defining the transition from weak-to-strong coupling.

Indeed, using fwhm’s in a strong coupling criterion is generally problematic. In disordered organic molecules such as MC the fwhm can be an unreliable estimate of lifetime. The fwhm of the absorption peak is often predominantly defined by the vibrational modes within the molecule which split the excitation into many closely spaced modes.5,27,28 Furthermore, a criterion for strong coupling that uses fwhm’s will be dependent upon the measurement apparatus, not just the system under interrogation. For oblique angles of incidence the measured fwhm’s of modes differ depending upon whether spectra are fixed-θ or fixed-k// (compare Figures 5a and b; the measured value of fwhm will depend on how the red line corresponding to the measured spectrum intersects any resonances). Additionally, it is sometimes simply not possible to characterize the uncoupled modes of a system.29 It seems that the most commonplace criteria for strong coupling are somewhat limited since they rely on comparisons of fwhm’s and Rabi splitting.

How else can we characterize the transition from weak-to-strong coupling? Ideally, a criterion for strong coupling should not be dependent upon the measurement technique. If a system is in the strong coupling regime this should clearly be apparent in multiple measuring techniques. Spectroscopic ellipsometry allows one to observe signatures of strong coupling in both amplitude and phase measurements. The formation of the secondary loop in Figure 3 corresponds to the point at which the amplitude and phase signatures of strong coupling are both observed. In Figures 5c the difference between Ω required for the Savona et al. criterion and secondary loop formation is 10%. This is less than the difference (12%) between the experimental and calculated values of Ω at the point of secondary loop formation, suggesting that the two criteria have a similar level of stringency. The secondary loop criterion has two advantages over the Savona et al. criterion. First, it is not dependent upon the approximation that losses can be equated with fwhm; second, while it can be impossible to determine if the Savona et al. criterion has been fulfilled in high-loss systems, observing the secondary loop in ellipsometry (a very low-noise technique) is straightforward. Furthermore, verifying the existence of a secondary loop in spectroscopic ellipsometry requires one to take just one measurement at a single angle. For these reasons, we suggest that studying the ellipsometric topology of a system and observing a secondary loop in ρ could perhaps provide an alternative and useful criterion for strong coupling.

4. Conclusions

We have studied the transition from the weak to strong coupling regime in a MC microcavity using spectroscopic ellipsometry and observed a signature for strong coupling in the ellipsometric phase response. The combination of amplitude and phase data produces a topologically distinct feature that we associate with strong coupling. The observation of this feature for strong coupling of both molecular/microcavity and surface lattice resonance/guided mode structures suggests it is a more general signature of strong coupling. We have compared the emergence of this change in ellipsometric topology with existing criteria for strong coupling and suggest that ellipsometric topology could provide an alternative and useful criterion for strong coupling. In summary, our results suggest a new criterion for strong coupling that does not suffer from the limitations of existing strong coupling criteria. More widely, our results suggest that spectroscopic ellipsometry may provide a powerful probe with which to explore strong coupling.

Acknowledgments

The authors thank Vasyl G. Kravets, Gregory H. Auton, and Alexander N. Grigorenko for providing the surface lattice resonance/guided mode structure. P.A.T. and W.L.B. acknowledge the support of the European Research Council through Project Photmat (ERC-2016-AdG-742222: www.photmat.eu). W.J.T. and H.A.F. acknowledge financial support from the Engineering and Physical Sciences Research Council (EPSRC) of the United Kingdom via the EPSRC Centre for Doctoral Training in Metamaterials (EP/L015331/1).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c01963.

  • Fourier transmission spectroscopy schematic; MC transmittance spectrum; ellipsometry of uncoupled systems; strong coupling of surface lattice resonances and waveguide modes; review of strong coupling criteria (PDF)

Author Present Address

† H.A.F.: Department of Electronics and Nanoengineering, Aalto University, Tietotie 3, FI-00076 Espoo, Finland.

The authors declare no competing financial interest.

Notes

The research data supporting this publication are openly available from the University of Exeter’s institutional repository at: https://doi.org/10.24378/exe.2543.

Supplementary Material

nl0c01963_si_001.pdf (1.2MB, pdf)

References

  1. Khitrova G.; Gibbs H. M.; Kira M.; Koch S. W.; Scherer A. Vacuum Rabi splitting in semiconductors. Nat. Phys. 2006, 2, 81. 10.1038/nphys227. [DOI] [Google Scholar]
  2. Törmä P.; Barnes W. L. Strong coupling between surface plasmon polaritons and emitters: a review. Rep. Prog. Phys. 2015, 78, 013901 10.1088/0034-4885/78/1/013901. [DOI] [PubMed] [Google Scholar]
  3. Tame M. S.; et al. Quantum plasmonics. Nat. Phys. 2013, 9, 329. 10.1038/nphys2615. [DOI] [Google Scholar]
  4. Weisbuch C.; Nishioka M.; Ishikawa A.; Arakawa Y. Observation of the coupled exciton-photon mode splitting in a semiconductor quantum microcavity. Phys. Rev. Lett. 1992, 69, 3314. 10.1103/PhysRevLett.69.3314. [DOI] [PubMed] [Google Scholar]
  5. Lidzey D. G.; et al. Strong exciton–photon coupling in an organic semiconductor microcavity. Nature 1998, 395, 53. 10.1038/25692. [DOI] [Google Scholar]
  6. Schwartz T.; Hutchison J. A.; Genet C.; Ebbesen T. W. Reversible switching of ultrastrong light-molecule coupling. Phys. Rev. Lett. 2011, 106, 196405. 10.1103/PhysRevLett.106.196405. [DOI] [PubMed] [Google Scholar]
  7. Bellessa J.; Bonnand C.; Plenet J. C.; Mugnier J. Strong coupling between surface plasmons and excitons in an organic semiconductor. Phys. Rev. Lett. 2004, 93, 036404. 10.1103/PhysRevLett.93.036404. [DOI] [PubMed] [Google Scholar]
  8. Fofang N. T.; et al. Plexcitonic nanoparticles: plasmon- exciton coupling in nanoshell- J-aggregate complexes. Nano Lett. 2008, 8, 3481–3487. 10.1021/nl8024278. [DOI] [PubMed] [Google Scholar]
  9. Shalabney A.; George J.; Hutchison J.; Pupillo G.; Genet C.; Ebbesen T. W. Coherent coupling of molecular resonators with a microcavity mode. Nat. Commun. 2015, 6, 1–6. 10.1038/ncomms6981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Long J. P.; Simpkins B. S. Coherent coupling between a molecular vibration and Fabry–Perot optical cavity to give hybridized states in the strong coupling limit. ACS Photonics 2015, 2, 130–136. 10.1021/ph5003347. [DOI] [Google Scholar]
  11. Romero G.; Ballester D.; Wang Y. M.; Scarani V.; Solano E. Ultrafast quantum gates in circuit QED. Phys. Rev. Lett. 2012, 108, 120501. 10.1103/PhysRevLett.108.120501. [DOI] [PubMed] [Google Scholar]
  12. Stassi R.; Nori F. Long-lasting quantum memories: Extending the coherence time of superconducting artificial atoms in the ultrastrong-coupling regime. Phys. Rev. A: At., Mol., Opt. Phys. 2018, 97, 033823 10.1103/PhysRevA.97.033823. [DOI] [Google Scholar]
  13. Feist J.; Galego J.; Garcia-Vidal F. J. Polaritonic chemistry with organic molecules. ACS Photonics 2018, 5, 205–216. 10.1021/acsphotonics.7b00680. [DOI] [Google Scholar]
  14. Christopoulos S.; et al. Room-temperature polariton lasing in semiconductor microcavities. Phys. Rev. Lett. 2007, 98, 126405. 10.1103/PhysRevLett.98.126405. [DOI] [PubMed] [Google Scholar]
  15. Berkhout A.; Koenderink A. F. Perfect absorption and phase singularities in plasmon antenna array etalons. ACS Photonics 2019, 6, 2917–2925. 10.1021/acsphotonics.9b01019. [DOI] [Google Scholar]
  16. Kravets V. G.; et al. Singular phase nano-optics in plasmonic metamaterials for label-free single-molecule detection. Nat. Mater. 2013, 12, 304. 10.1038/nmat3537. [DOI] [PubMed] [Google Scholar]
  17. Berkovic G.; Krongauz V.; Weiss V. Spiropyrans and spirooxazines for memories and switches. Chem. Rev. 2000, 100, 1741–1754. 10.1021/cr9800715. [DOI] [PubMed] [Google Scholar]
  18. Tompkins H.; Irene E. A.. Handbook of Ellipsometry; William Andrew Publishing: 2005. [Google Scholar]
  19. Greet R.; Wind M. M. Polar representation of ellipsometric data. Appl. Opt. 1986, 25, 1627–1629. 10.1364/AO.25.001627. [DOI] [PubMed] [Google Scholar]
  20. Ehrenreich H.; Philipp H. R. Optical properties of Ag and Cu. Phys. Rev. 1962, 128, 1622. 10.1103/PhysRev.128.1622. [DOI] [Google Scholar]
  21. Dovzhenko D. S.; Ryabchuk S. V.; Rakovich Y. P.; Nabiev I. R. Light–matter interaction in the strong coupling regime: configurations, conditions, and applications. Nanoscale 2018, 10, 3589–3605. 10.1039/C7NR06917K. [DOI] [PubMed] [Google Scholar]
  22. Thomas P. A.; Auton G. H.; Kundys D.; Grigorenko A. N.; Kravets V. G. Strong coupling of diffraction coupled plasmons and optical waveguide modes in gold stripe-dielectric nanostructures at telecom wavelengths. Sci. Rep. 2017, 7, 45196. 10.1038/srep45196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Sparrow C. M. On spectroscopic resolving power. Astrophys. J. 1916, 44, 76. 10.1086/142271. [DOI] [Google Scholar]
  24. Savona V.; Andreani L. C.; Schwendimann P.; Quattropani A. Quantum well excitons in semiconductor microcavities: Unified treatment of weak and strong coupling regimes. Solid State Commun. 1995, 93, 733–739. 10.1016/0038-1098(94)00865-5. [DOI] [Google Scholar]
  25. Bender C. M.; Boettcher S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. 10.1103/PhysRevLett.80.5243. [DOI] [Google Scholar]
  26. Frisk Kockum A.; Miranowicz A.; De Liberato S.; Savasta S.; Nori F. Ultrastrong coupling between light and matter. Nat. Rev. Phys. 2019, 1, 19. 10.1038/s42254-018-0006-2. [DOI] [Google Scholar]
  27. Houdré R.; Stanley R. P.; Ilegems M. Vacuum-field Rabi splitting in the presence of inhomogeneous broadening: Resolution of a homogeneous linewidth in an inhomogeneously broadened system. Phys. Rev. A: At., Mol., Opt. Phys. 1996, 53, 2711–2715. 10.1103/PhysRevA.53.2711. [DOI] [PubMed] [Google Scholar]
  28. Fidder H.; Knoester J.; Wiersma D. A. Optical properties of disordered molecular aggregates: A numerical study. J. Chem. Phys. 1991, 95, 7880–7890. 10.1063/1.461317. [DOI] [Google Scholar]
  29. Brimont C.et al. Strong coupling of exciton-polaritons in a bulk GaN planar waveguide: quantifying the Rabi splitting 2020. arXiv (Condensed Matter, Mesoscale and Nanoscale Physics), February 12, 2020, 2002.05066, ver. 2. https://arxiv.org/abs/2002.05066 (accessed 2020-07-22).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c01963_si_001.pdf (1.2MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES