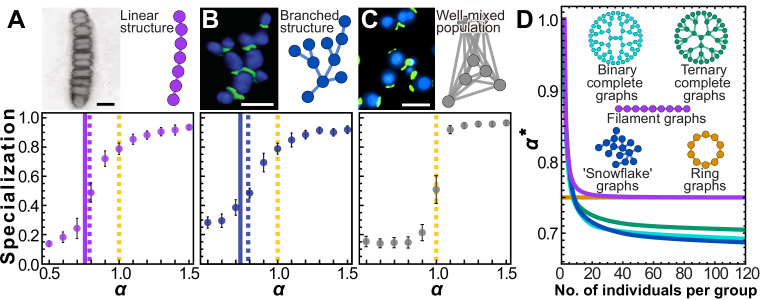
Figure 4. Simple multicellular organisms with sparse topologies.

We show two examples of simple multicellular organisms with linear and branched topologies. The image in (A) is a fossilized rhodophyte specimen of Bangiomorpha pubescens, courtesy of Prof. Nicholas Butterfield (see e.g. Butterfield, 2000); the image in (B) is a confocal image of ‘snowflake yeast’ showing cell volumes in blue and cell-cell connections in green; the image in (C) is an epifluorescence image of individual yeast cells from a planktonic culture, with the same staining technique as in (B). Scale bars in pictures = 10 µm. Panels include cartoons depicting simplified topologies. Topologically similar to the two-neighbor configuration, these configurations yield similar simulation results. Specialization is plotted as a function of α. Solid (A) and blue (B) vertical lines (A and B) indicate analytical solutions for the transition point where the Hessian evaluated at ${\displaystyle \overrightarrow{v}=\frac{1}{2}\overrightarrow{1}}$ stops being negative definite, that is, ${\alpha }^{*}$; dotted lines indicate roughly where the simulation curves cross specialization of 0.5, that is, the 'true' transition value of α where specialization becomes favored. (C) In contrast, for a well-mixed group with fully connected topology, ${\displaystyle {\alpha }^{\ast }=0.5}$, indicating specialization only occurs when there are accelerating returns on investment. (D) To further explore trees and filaments we analytically solved for ${\alpha }^{*}$ for various types of trees and filaments of different sizes. ${\alpha }^{*}$ is plotted versus group size for several topologies. This is a proxy measure of how amenable a network structure is to specialization.

Prof. Butterfield has granted permission to distribute the image in panel A under the terms of a Creative Commons Attribution license [https://creativecommons.org/licenses/by/4.0/]; further reproduction of this image should adhere to the terms of the CC BY 4.0 license with an attribution to Prof. Butterfield.