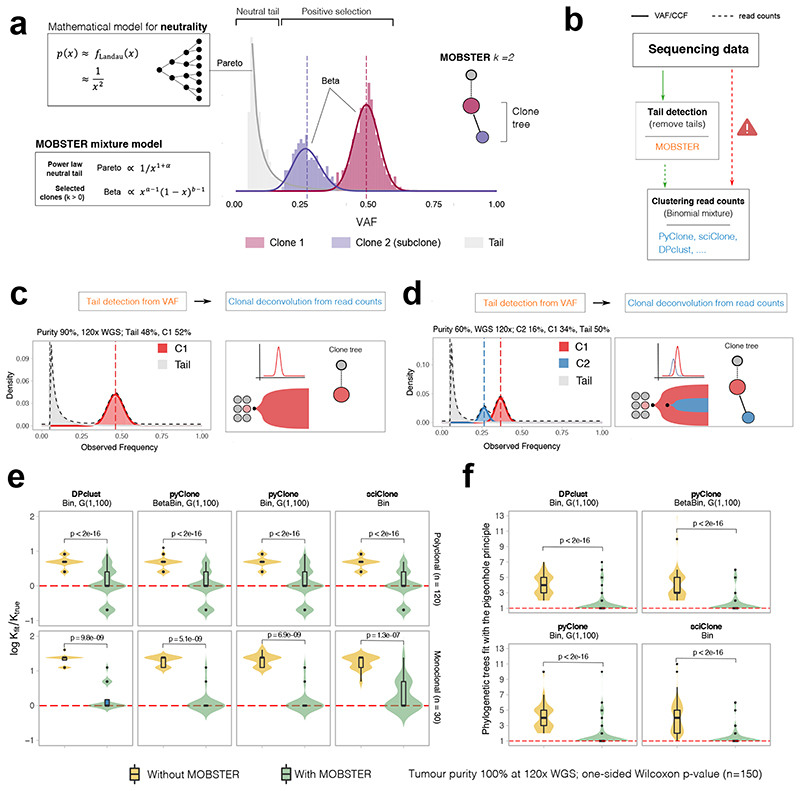
Figure 2. Model-based tumor subclonal reconstruction.

(a) MOBSTER combines a Pareto Type-I distribution with k Beta random variables into a univariate finite mixture with k+1 components. The Pareto captures the frequency spectrum of neutral mutations predicted by theory (Landau distribution decaying as 1/f ²), whereas Beta components detect alleles under positive selection. The histogram shows clustering assignments for a tumor with one selected subclone (k=2). (b) MOBSTER filters out neutral tail mutations, and one can cluster the rest with any tool for subclonal reconstruction using read counts. CCF, cancer cell fraction. (c, d) MOBSTER applied to the examples in Figure 1a,b detects the clusters corresponding to the true selected clones, hence recovering the correct clonal architecture. WGS, whole genome sequencing (e,f) We used synthetic 120x WGS data from n=150 simulated tumors to compare current methods with MOBSTER (plots show mean and inter quartile range IQR, upper whisker is 3rd quartile +1.5 * IQR and lower whisker is 1st quartile −1.5 * IQR). We measured how many clusters (e) and clone trees we identify (f). Tests compare Binomial mixtures from DPclust, pyClone and sciClone, and Beta-Binomial mixtures from pyClone, parameterized by concentration α > 0. DPclust and pyClone learn α from the data assuming a Gamma prior. sciClone is a variational method with hardcoded α. In (e) we report the logarithm of the ratio between the number of subclones found by MOBSTER (k _fit) and the true number of clones (k _true). Red dashed line represents k_fit = k_true. In (f) we plot the number of trees that can be fit by pigeonhole principle using the output of each tool.