A surface-free design for phase I dual-agent combination trials

Abstract

In oncology, there is a growing number of therapies given in combination. Recently, several dose-finding designs for Phase I dose-escalation trials for combinations were proposed. The majority of novel designs use a pre-specified parametric model restricting the search of the target combination to a surface of a particular form. In this work, we propose a novel model-free design for combination studies, which is based on the assumption of monotonicity within each agent only. Specifically, we parametrise the ratios between each neighbouring combination by independent Beta distributions. As a result, the design does not require the specification of any particular parametric model or knowledge about increasing orderings of toxicity. We compare the performance of the proposed design to the model-based continual reassessment method for partial ordering and to another model-free alternative, the product of independent beta design. In an extensive simulation study, we show that the proposed design leads to comparable or better proportions of correct selections of the target combination while leading to the same or fewer average number of toxic responses in a trial.

1. Introduction

A common goal of Phase I clinical trials is to find a treatment which has a pre-specified toxicity risk, γ. Some drugs can be more efficient in combination with other compounds.¹ Therefore, there is a need for Phase I doseescalation designs aiming to find the maximum tolerated combination (MTC). In contrast to single-agent trials, combination trials can suffer from the uncertainty in the monotonic toxicity ordering for some of the combinations, due to the natural absence of complete ordering – in a mathematical sense – between pairs of doses.

Several designs for combination trials have been proposed in the literature, e.g. rule-based designs,² modelbased designs,^3–5 partial ordering continual reassessment methods (POCRM),⁶ and the approaches that do not use parametric assumptions on the combination-toxicity model.^7–11 We refer the reader to the recent reviews by Hirakawa et al.¹² and Riviere et al.¹³ that study the properties of several dose-finding designs for dualcombination studies under many different scenarios.

The majority of them face some drawbacks and practical limitations. First, parametric model-based approaches, reviewed by Gasparini,¹⁴ restrict the search of the MTC to a particular surface and, therefore, one can expect that they are not able to find the MTC with high probability in some unexpected cases. They are excluded from further discussion in this work, since we are aiming to less restrictive designs. The POCRM gives greater flexibility to an investigator, but requires a set of monotonic orderings to be specified before the trial. While there is a practical guide for the choice of orderings,^15,16 there is still a risk that all chosen orderings are far from the true one and, in addition, that a clinician is too cautious to randomise patients among different orderings, especially in the presence of a small sample size. In fact, current designs that do not use strong parametric assumptions on the combination–toxicity relationship might require randomisation⁷ for a better exploration of combinations, a task that can be undesirable for clinicians in an early phase escalation trial as well.

In this work, we propose a novel model-free design that employs the model-free idea by Gasparini and Eisele¹⁷ to parametrise ratios between combinations’ toxicity probabilities. Specifically, the proposed design parametrises all monotonic connections between neighbouring combinations. The proposal relies on the monotonicity assumption within one compound and does not require randomisation or any orderings to be pre-specified in a trial. The distinguishing feature of the novel design is to parametrise “connections” (ratios) between toxicity probabilities rather than probabilities themselves as was proposed for model-free designs previously.⁷ We compare the proposed design to the model-free design PIPE (product of independent beta)⁷ and the model-based POCRM design.⁶ We show that, despite the assumptions the model employs and a number of parameters to be estimated, it provides great flexibility in dual-agent studies compared to these alternatives, leading to better operating characteristics in many scenarios. We also address the question of appropriate choices of prior distributions in detail.

In Section 2 we recall the original curve-free design for the single-agent setting¹⁷ and generalise the idea to dual-agent combination trials. An illustration of the proposed design is provided in Section 3 and a comparison of the proposed design to other methods is provided in Section 4. We conclude with a discussion in Section 5.

2. Methods

2.1. Curve-free design for single-agent trials

Gasparini and Eisele¹⁷ proposed the following design for single-agent oncology trials that requires only the assumption of monotonicity. Consider a trial with m doses, N patients and a binary toxicity outcome. The goal of the trial is to find the maximum tolerated dose (MTD) corresponding to the maximum acceptable probability of toxicity γ. Let p_i be the probability to experience toxicity given dose i. It is assumed that the monotonicity assumption, p ₁ ≤ p ₂ ≤ … ≤ p_m, holds. The statistical model was parameterised as θ ₁ = 1 − p ₁, ${\theta }_2=\frac{1-p_2}{1-p_1},\dots ,{\theta }_m=\frac{1-p_m}{1-p_{m-1}}$ where θ_i i = 1,…,m are independent random variables with Beta prior distribution 𝓑(a_i,b_i). Then, the toxicity probability corresponding to dose i can be written as

$$p_i=1-{\theta }_1{\theta }_2\dots {\theta }_i$$ (1)

This parametrisation implies that “connections” between neighbouring doses are modelled independently, while, as natural for single-agent studies, the toxicity probabilities are dependent. This leads to the consideration of infinitely many possible shapes of the dose-toxicity relation. The proposed approach does imply a model on the dose–toxicity relationship but does not restrict its search to a particular parametric curve, and, consequently, was called “curve-free”. The modelling of connections was motivated by the sequential nature of dose-finding trials: at each step, one typically looks forward to model the connection between the neighbouring doses, the current dose-level and the next higher dose-level.

Let x_i, i = 1, … m be the number of patients who experienced a toxicity response among n_i patients treated on ith dose, and $n={\displaystyle {\sum }_i{n}_i}$ patients have been already assigned in the trial. Then the likelihood function is a product of binomial terms

$$ℒ({\theta }_1,\dots ,{\theta }_m)=\underset{i=1}{\overset{m}{{{\displaystyle \prod }}^{\text{}}}}{\left(p_i({\theta }_1,\dots ,{\theta }_i)\right)}^{x_i}{\left(1-p_i({\theta }_1,\dots ,{\theta }_i)\right)}^{n_i-x_i}$$

Applying Bayes’ theorem, one can get the posterior distribution

$$\pi \left({\theta }_1,\dots ,{\theta }_m\mid \text{data}\right)\propto ℒ\left({\theta }_1,\dots ,{\theta }_m\right)\pi \left({\theta }_1,\dots ,{\theta }_m\right)$$

where π(θ ₁,…, θ_m) is a prior distribution of (θ ₁,…, θ_m). This results in the posterior distributions for all θ_i that are used to obtain 𝔼(p_i); i = 1,…,m. The dose i satisfying arg min_i|𝔼(p_i|data) − γ| is selected for the next group of patients. The designs proceeds until the prespecified maximum number of patients, N, have been treated.

2.2. Surface-free parametrisation

Consider now a dual-agent combination trial with I dose levels of drug A, J levels of drug B and I × J combinations studied in the trial. Let p_ij be the toxicity probability of the combination of the ith dose of A and the jth dose of B. The goal of the study is to find the maximum tolerated combination (MTC) defined as the combination having the probability of toxicity closest to the target toxicity γ.

Similar to the original motivation, a combination dose-finding trial is sequential in nature: at each step, one typically looks forward to model the connections between the neighbouring combinations, the current one and the combinations with one dose-level higher for one of the agents. Therefore, the idea of the proposed parametrisation is to model the ratios between combinations. Let θ be a probability of not observing a toxicity given the first combination (1, 1), θ = 1 − p ₁₁, and let ${\theta }_i^{(j)}$ be the ratio between the probabilities of not observing a toxicity between neighbouring combinations having the i-th and the (i − 1)-th doses of A while keeping the j-th dose of B fixed

$${\theta }_i^{(j)}=\frac{1-p_{i,j}}{1-p_{i-1,j}},i=2,\dots ,I,j=1,\dots ,J$$ (2)

Similarly, let ${\tau }_j^{(i)}$ be the ratio between the probabilities of not observing a toxicity between neighbouring combinations having the j-th and the (j − 1)-th doses of B while keeping the i-th dose of A fixed

$${\tau }_j^{(i)}=\frac{1-p_{i,j}}{1-p_{i,j-1}},i=1,\dots ,I,j=2,\dots ,J$$ (3)

Note that equations (2) and (3) do not include the parametrisation between diagonal elements, since the ratio between any two diagonal combinations can be explicitly found as

$$\frac{1-p_{i,j}}{1-p_{i-1,j-1}}=\frac{1-p_{i,j}}{1-p_{i-1,j}}\frac{1-p_{i-1,j}}{1-p_{i-1,j-1}}={\theta }_i^{(j)}\times {\tau }_j^{(i-1)}={\tau }_j^{(i)}\times {\theta }_i^{(j-1)}$$ (4)

Moreover, from equation (4), one can write

$${\theta }_i^{(j)}={\theta }_i^{(j-1)}\times {\tau }_j^{(i)}/{\tau }_j^{(i-1)}$$ (5)

so that it is sufficient to specify ${\theta }_i^{(j)}$ for j = 1 only and i = 2,…, I, while keeping ${\tau }_1^{(i)}$ for i = 1; … ; I and j = 2,…, J.

Thus, we adopt the notation ${\theta }_i^{(j)}$. This way, many redundant connections have been removed, and I×J parameters remain. We refer to the parametrisation above as to the “surface-free” one (mimicking to the original “curve-free” name by Gasparini and Eisele¹⁷), as it does not restrict the search of the combination–toxicity relationship to a particular surface defined by a parametric function.

Due to the limited sample size in Phase I clinical trials, it can be challenging to estimate all the I×J parameters. To reduce the complexity of the estimation problem, we impose the no-interaction assumption, which implies that additional toxicity added by increasing the amount of drug A (B) by one dose level is the same for any amount of drug B (A). Formally, we have the following definition.

Definition 1 The toxicity probabilities defined by equations (2), (3) and (5) are said to specify a no-interaction model if ${\tau }_j^{(1)}={\tau }_j^{(2)}=\cdots ={\tau }_j^{(I)}:={\tau }_j$ for each j = 2; … ; J.

We then have the following result.

Theorem 1 Under the no-interaction model, the toxicity probability p_ij for any (i, j) can be written as

$$p_{ij}=1-\theta {\theta }_2\dots {\theta }_i{\tau }_2\dots {\tau }_j$$ (6)

The proof amounts to checking that ratios between any two diagonal combinations can be found explicitly as $\frac{1-p_{i,j}}{1-p_{i-1,j-1}}={\theta }_i\times {\tau }_j$ due to the no-interaction assumption. By finite induction, expression (6) is the same for any escalation path reaching (i, j).

Expression (6) corresponds to moving along the row until reaching column j and then along the column until row i. It is easy to see that the assumption of monotonicity within one agent is guaranteed, while no strict assumptions on the relation between the “anti-diagonal” combination are made (e.g. on p ₁₂ and p ₂₁). Moreover, the proposed parametrisation avoids assuming any pre-specified orderings between these combinations and results in I + J − 1 ratios, which simplifies the estimation problem noticeably. It is important to mention that while, in general, the compounds in a dose-finding study are expected to interact, the no-interaction model above is a working assumption that has shown its usefulness in some dose-finding settings with small sample sizes, e.g. in a setting considering toxicity and efficacy endpoints.¹⁸ We will demonstrate that the no-interaction assumption does not prevent selecting the MTC with high probability when there is an interaction in the compounds’ toxicities. We have also found that the model with all interactions requires additional restrictions to satisfying the monotonicity assumption and is highly unstable. Consequently, we focus on the no-interaction version of the proposed parameterisation.

Note that δ_i; τ_j ∈ (0, 1) for all i, j due to the monotonicity assumption within one compound. If we then additionally assume that δ_i; τ_j are independent Beta random variables with parameters 𝓑(a_i, b_i) and 𝓑(e_j, f_j), respectively, a_i, b_i, e_j, f_j > 0, these prior marginals then induce a joint prior probability distribution π(p ₁₁,…, p_{I ,J}) on the vector of toxicity probabilities. The robustness of the design to this joint prior distribution and the recommendations for its specifications are discussed in Section 3 and in the Supplementary Materials. The distribution induced by equation (6) is called a product-of-beta.¹⁷ Let x_ij, i = 1,…, I, j = 1,… J be the number of patients experiencing toxicity among n_ij patients treated at the ijth combination so that $n={\displaystyle {\sum }_{i,j}{n}_{ij}}$ patients are observed. Then, the likelihood function takes the form

$$ℒ\left(\theta ,{\theta }_2,\dots ,{\theta }_I,{\tau }_2,\dots ,{\tau }_J\right)=\underset{i=1}{\overset{I}{{{\displaystyle \prod }}^{\text{}}}}\underset{j=1}{\overset{J}{{{\displaystyle \prod }}^{\text{}}}}{p}_{ij}^{x_{ij}}{\left(1-p_{ij}\right)}^{n_{ij}-x_{ij}}$$

Applying Bayes theorem, one can get the posterior distribution

$$\pi \left(\theta ,{\theta }_2,\dots ,{\theta }_I,{\tau }_2,\dots ,{\tau }_J\mid \text{data}\right)\propto ℒ\left(\theta ,{\theta }_2,\dots ,{\theta }_I,{\tau }_2,\dots ,{\tau }_J\right)\pi \left(\theta ,{\theta }_2,\dots ,{\theta }_I,{\tau }_2,\dots ,{\tau }_J\right)$$

which can be used in the subsequent analysis.

Similar to the original single-agent proposal, the parameterisation (6) and the model above exploits the assumption of independence of the toxicity increments (ratios) rather than toxicity probabilities themselves that are naturally expected to be dependent. Furthermore, the proposed model bares one more important property on the toxicity probabilities. The consecutive multiplication of Beta random variables implies that the variance of the toxicity probability increases as the dose of the agent increases. This reflects the reality of most Phase I clinical settings: one typically knows more about lower combinations and has more uncertainty about higher combinations. The greater variance at higher doses allows for more cautious escalations. Different levels of uncertainty implied by the proposed model will be explicitly shown in the illustrative example in Section 3.

2.3. Generalisation to combination with more than two agents

The idea of parameterising connections between neighbouring combinations can be straightforwardly extended to multi-agent combinations as long as the monotonicity assumption within each drug is satisfied. For instance, in case of three agent combinations with I doses of drug A, J doses of drug B and K doses of drug C, to parametrise a probability of toxicity corresponding to combination (i, j, k), p_i,j,k, one needs to define under the no-interaction assumption

$${\theta }_i=\frac{1-p_{i,j,k}}{1-p_{i-1,j,k}}\text{for}i=2,\dots ,I,j=1,\dots ,J,k=1,\dots ,K,$$

$${\tau }_j=\frac{1-p_{i,j,k}}{1-p_{i,j-1,k}},\text{for}i=1,\dots ,I,j=2,\dots ,J,k=1,\dots ,K,$$

and

$${\nu }_k=\frac{1-p_{i,j,k}}{1-p_{i,j,k-1}},\text{for}i=1,\dots ,I,j=1,\dots ,J,k=2,\dots ,K.$$

This results in I + J + K − 1 parametrised connections. Generally, in a combinationXstudy with R agents with K_r dose levels for drug r, r = 1,…, R, the proposed parametrisation would result in ${\displaystyle {\sum }_r^R=K_r-1}$ connections. Despite a greater number of parameters, the estimation procedure and the dose-escalation design remain the same. The novel design in case of two agents is proposed below.

2.4. Surface-free design

We propose the following dose-finding design for dual-agent combination trials. Consider a trial aiming to find the MTC corresponding to the target toxicity probability γ with N number of patients and m combinations based on I and J dose levels per agent. Patients are assigned cohort-by-cohort where the cohort is a small group of 1 to 5 patients. Before starting the trial, prior Beta distributions are to be defined. If clinicians have some prior knowledge about the compounds’ toxicities to be included in the design of a trial, there are two ways how this information can be incorporated using the design proposed. For the first approach, assume that some prior mean estimates of the toxicity probabilities, for example, ${\widehat{p}}_{11}(0),{\widehat{p}}_{12}(0)\dots ,{\widehat{p}}_{I-1,J}(0),{\widehat{p}}_{I,J}(0)$, are provided by a clinician. One starts from the elicitation of the prior parameters a_i, b_i, e_j, f_j by matching the mean estimates and an effective sample size for all i, j

$$p_{ij}=1-\frac{a_1}{a_1+b_1}\frac{a_2}{a_2+b_2}\cdots \frac{a_i}{a_i+b_i}\frac{e_1}{e_1+f_1}\cdots \frac{e_j}{e_j+f_j}$$ (7)

$$a_i+b_i=c_i,e_j+f_j=t_j$$ (8)

where c_i, t_j are the effective sample sizes of prior distributions. The elicitation proceeds sequentially starting from the parameters a ₁, b ₁ corresponding to the lowest combination probability p ₁₁ and ending at the parameter e_J, f_J. Clearly, under the no-interaction assumption, it is possible that the proposed parametrisation cannot provide an exact match for the prior toxicity probabilities at all combinations. In this case, the parameters that reassamble the prior toxicity probabilities as close as possible, for example, in terms of the sum of squared distances, are selected.

The second approach concerns the cases when clinicians provide toxicity estimates for each agent individually. Let ${\widehat{p}}_{10}(0),\dots ,{\widehat{p}}_{10}(0)$ be the prior point estimates of the toxicity probabilities of the first agent administered as a monotherapy, and let ${\widehat{p}}_{01}(0),\dots ,{\widehat{p}}_{0J}(0)$ be the prior point estimates of the toxicity probability for the second agent given as a monotherapy. The prior mean values of θ_i and τ_j could be found as ${\widehat{\theta }}_i(0)=\frac{1-{\widehat{p}}_{i,0}(0)}{1-{\widehat{p}}_{i-1,0}(0)}$ and ${\widehat{\tau }}_j(0)=\frac{1-{\widehat{p}}_{0,j}(0)}{1-{\widehat{p}}_{0,j}(0)}$. The parameter corresponding to the lowest combination under no-interaction parametrisation

$$\widehat{\theta }(0)=1-{\widehat{p}}_{1,0}-{\widehat{p}}_{0,1}+{\widehat{p}}_{1,0}\times {\widehat{p}}_{0,1}$$

Importantly, under both cases above, the performance of the design can noticeably depend on the specification of the effective sample size parameters c_i; t_j, and their careful selection is required to avoid an unstable behaviour.¹⁹ In Section 3.3, we provide guidance on how these parameters can be selected to provide a robustness performance of the proposed design.

Let ${\widehat{\theta }}_i(0)$ and ${\widehat{\tau }}_j(0)$ be prior point estimates. Then, the probability of toxicity can be found as ${\widehat{p}}_{ij}(0)=1-\widehat{\theta }(0){\widehat{\theta }}_1(0)\dots {\widehat{\theta }}_i(0){\widehat{\tau }}_2(0)\dots {\widehat{\tau }}_j(0)$.Let $T\left({\widehat{p}}_i,\gamma \right)$ be a summary statistic for the combination (i, j) upon which the decision about selection is based. The combination (i*; j*) for which $T\left({\widehat{p}}_{ij},\gamma \right)$ is minimised among all combinations is selected for the next cohort of patients. Below, we consider the following decision criterion $T\left({\widehat{p}}_{ij},\gamma \right)=\left|{\widehat{p}}_{i,j}-\gamma \right|$. Iteratively, assume that x_ij patients out of n_ij experienced a toxicity after receiving combination (i, j) and n patients were enrolled. Then, the posterior distribution is updated and posterior means ${\widehat{\theta }}_i(n),{\widehat{\tau }}_j(n)$ are obtained. The estimate of toxicity probabilities can be found as ${\widehat{p}}_{ij}(n)=1-\widehat{\theta }(n){\widehat{\theta }}_1(n)\dots {\widehat{\theta }}_i(n){\widehat{\tau }}_2(n)\dots {\widehat{\tau }}_j(n)$. The combination i*; j* minimising $T\left({\widehat{p}}_{ij},\gamma \right)$ is selected for the next cohort of patients. The design proceeds until a preassigned number of patients N is achieved. We adopt the final selection as the final combination recommendation in the trial.

The design above aims to identify a single MTC (similar to the POCRM design⁶) as it assigns the next cohort of patients to the best estimated MTC and employs no randomisation. Below, we will mainly focus on this setting. At the same time, the proposed parameterisation can be used to find multiple MTCs. For this, a different allocation

rule should be used. In the Supplementary Materials, we study the performance of the proposed parameterisation when the objective of the trial is to find all MTCs defined as the combination with the toxicity probability within 5% of the target toxicity level of 20%. Then, using the same parameterisation for the toxicity probabilities, this version of the proposed design randomises the next cohort of patients to one of the combinations with the estimated toxicity between 15% and 25%.

2.5. Early stopping for toxicity

In an actual trial, the lowest combination could be found to have toxicity probability above the target and hence it cannot be recommended as the MTC. In this case, the trial should be terminated, and we implement a safety constraint to facilitate stopping the study.

Due to the monotonicity assumption, if the lowest combination has an unacceptable toxicity probability then all other combinations cannot be selected as well. Therefore, we put the restriction on the lowest combination. The trial is terminated if

$$\mathbb{P}\left(p_{11}>{\gamma }^{\ast }\mid \text{data}\right)>\zeta$$ (9)

where γ* is a toxicity threshold beyond which the toxicity is unacceptable and ζ is the threshold probability controlling the overdosing.

3. Illustration

In this section, we demonstrate the construction of the design by revisiting a Phase I clinical trial in advanced melanoma patients.²⁰ First, we will describe the original trial and demonstrate the elimination of ratios as proposed above. Second, we illustrate a prior elicitation algorithm given the information available before the combination trial. Finally, we demonstrate an escalation procedure in the individual and replicated trials.

3.1. Trial specification

The Phase I melanoma dose-escalation trial in Plimack et al.²⁰ studied combinations of two drugs, decitabine (drug A) and pegylated interferon (drug B), which was rationally selected for the clinical study based on preclinical data showing the synergistic antitumor activity of the combination of the two agents. Importantly, both agents were studied independently in single-agent clinical trials for a relatively long time, which provided extensive information on the prior estimates. Decitabine was given intravenously over 1 h daily for five days, on days 1–5 during a 28-day treatment cycle, and pegylated interferon was given by subcutaneous injection once weekly during the same cycle.²⁰ Three dose levels of decitabine were studied in the combination trial (mg/m₂/day): 5, 10, 15 (denoted by A ₁, A ₂ and A ₃); and three dose levels of Pegylated interferon α-2 b lg/kg: 1.5, 3 and 4.5 (denoted by B ₁, B ₂, B ₃). These dose levels result in 3 × 3 = 9 possible dual-agent combinations. However, only four combinations (that could be certainty ordered according to increasing toxicity) were chosen for the study. Consequently, a variation of the 3 design was applied to lead the dose-escalation procedure.

In fact, one could avoid choosing a subset of combinations by applying the proposed dose-escalation design which allows for the escalation of both agents simultaneously. Below, we demonstrate how one can apply the novel design to such a trial given the prior information available before the study. The goal of the trial is to find the MTC corresponding to γ = 0.30. As the original trial with four combinations used 17 patients, we will consider the total sample size of N = 36 and nine combinations preserving nearly the same patient/combination ratio. As in the original trial, cohorts of three patients are used before an escalation decision is made.

3.2. Parametrisation and elimination of connections

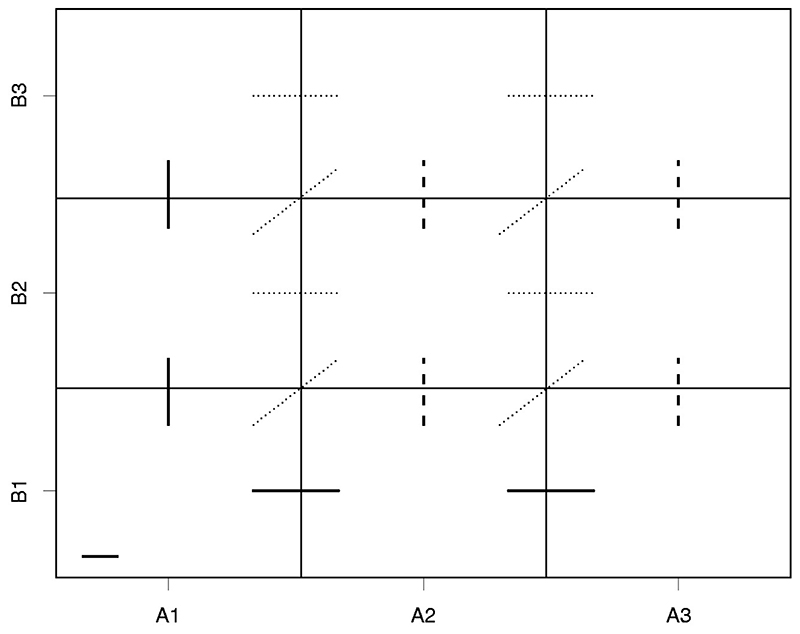
Nine possible combinations can be schematically presented as in Figure 1.

Figure 1. All monotonic connections between neighboring combinations in 3 by 3 example.

Each rectangle corresponds to the combination of the respective dose levels of agent A and agent B. For instance, the left bottom corner corresponds to the combination consisting of dose A ₁ of the agent A and dose B ₁ of the agent B. Following the proposed design, one needs to parameterise the probability of no toxic response at the lowest combination (A ₁, B ₁) as a Beta random variable θ (denoted by a solid horizontal line in the left bottom corner).

The next step is to parameterise the connections between neighbouring combinations as proposed above. Based on the assumption of monotonicity within one agent, note that there are 17 known monotonic connections between neighbouring combinations denoted by solid, dashed and dotted lines in Figure 1. However, as noted in Section 2.2, the majority of these connections can be eliminated. First, following equation (4), one can rewrite the diagonal corrections. For instance, moving from combination (A ₁,B ₁) to (A ₂,B ₂) is equivalent to moving from (A, B) to (A, B) and then from (A, B) to (A, B). In the introduced notations, $\frac{1-p_{2,2}}{1-p_{1,1}}={\theta }_2^{(1)}\times {\tau }_2^{(2)}$. Second, using equation (5), one can rewrite horizontal connections corresponds to dose levels B ₂ and B ₃. For instance, the ratio between combinations (A, B) and (A, B) can written as ${\theta }_2^{(2)}={\theta }_2^{(1)}\times {\tau }_2^{(2)}/{\tau }_2^{(1)}$. Following the same logic, the remaining horizontal connections denoted by dotted lines can be written. This results in nine connections left. Finally, following the no-interaction assumption, we eliminate the connections denoted by dashed lines. For instance, this means that ${\theta }_2^{(1)}={\theta }_2^{(2)}$ and so on. As a result, five ratios remain.

3.3. Prior elicitation

In oncology combinational trials, clinicians usually have reliable prior knowledge about toxicity risks for each compound given as a monotherapy. Using this prior knowledge and the monotonicity assumption, one can compute prior estimates of toxicity probabilities for all combinations. We demonstrate this procedure applied to the melanoma trial.

Denote by ${\widehat{\mathbf{\text{p}}}}^{(A)}(0)={\left[{\widehat{p}}_1^{(A)},\dots ,{\widehat{p}}_I^{(A)}\right]}^{\text{T}}$ and ${\widehat{\mathbf{\text{p}}}}^{(B)}(0)={\left[{\widehat{p}}_1^{(B)},\dots ,{\widehat{p}}_J^{(B)}\right]}^{\text{T}}$ prior estimates of toxicity probabilities provided by clinician for I doses of drug A and J doses of drug B given as monotherapies, respectively. Following the prior information that was used by Yuan and Yin²¹ who used the same example and given previously clinical trials of the compounds,²² we assume the following prior mean estimates of the toxicity probabilities for three dose levels of each drug: ${\widehat{\mathbf{\text{p}}}}^{(A)}(0)={\left[0.05,0.10,0.20\right]}^T$ and ${\widehat{\mathbf{\text{p}}}}^{(B)}(0)={\left[0.05,0.10,0.20\right]}^T$. The probability of no toxic response at the lowest combination can then be found as $\widehat{\theta }(0)=1-0.10-0.05+0.10\times 0.05=0.855$. Further, using the prior information about agent A given as a monotherapy, one can obtain that

$${\widehat{\theta }}_2(0)=\frac{1-{\widehat{p}}_2^{(A)}}{1-{\widehat{p}}_1^{(A)}}=\frac{1-0.10}{1-0.05}\approx 0.947,{\widehat{\theta }}_3(0)=\frac{1-0.2}{1-0.1}\approx 0.888$$

and for the agent B,

$${\widehat{\tau }}_2(0)=\frac{1-{\widehat{p}}_2^{(B)}}{1-{\widehat{p}}_1^{(B)}}=\frac{1-0.20}{1-0.10}\approx 0.899,{\widehat{\tau }}_3(0)=\frac{1-0.30}{1-0.20}=0.875$$

This, however, defines the mean values only. To define parameters a_i, b_i, e_j, f_j uniquely, one needs to choose the effective sample sizes c_i, t_j, which define the uncertainty about the corresponding ratio. Using equation (8) and the obtained mean values for prior estimates, one can find an explicit expression for parameters a_i, b_i and e_j, f_j in terms of c_i and t_j, respectively,

$$a_i=c_i{\theta }_i,b_i=c_i\left(1-{\theta }_i\right)\text{and}{e}_j=t_j{\tau }_j,f_j=t_j\left(1-{\tau }_j\right)$$

Following the discussions on model-free designs,¹⁹ we investigate the impact of the effective sample size choice in more detail.

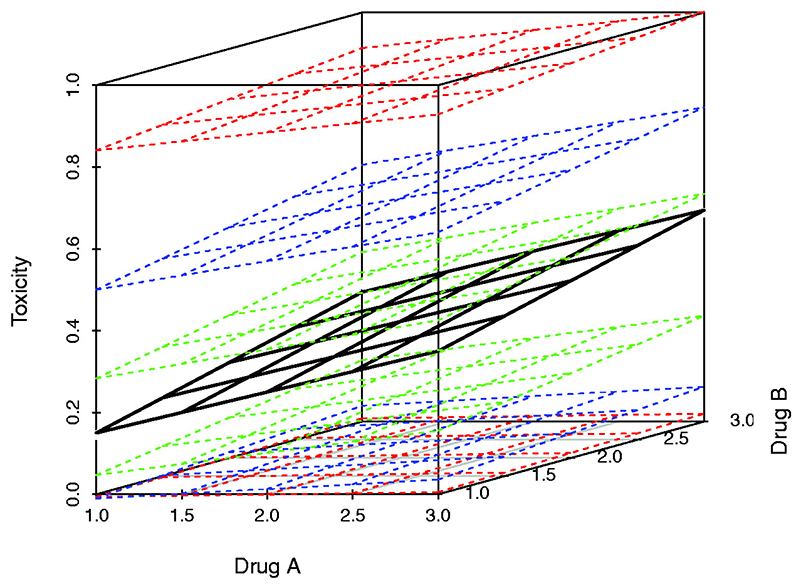
To illustrate the roughness of the prior distribution, we would consider the toxicity probabilities on the plane given in Figure 2.

Figure 2. Mean estimates and 90% credible intervals for prior toxicity estimates for different values of c = 1 (red), c =4 (blue) and c = 25 (green).

The black surface corresponds to prior mean estimates of toxicity probability for each dose of drugs A and B. It is assumed that a clinician has the same amount of uncertainty in each ratio, so c ₁ = c ₂ = c ₃ = t ₂ = t ₃ = c. The 90% confidence interval for prior toxicity probability estimates are given for c = 1 (red), c = 4 (blue) and c = 25 (green). Note that c = 1 corresponds to the least informative prior among the considered ones. While it is expected that a less informative prior would affect the procedure less, this choice of prior, however, can be excessively “vague” given the setting of a Phase I trial with small sample size. Let us consider two data points for the lowest and highest combinations to illustrate it.

The choice c = 1 implies that 90% credible interval for p ₁₁ is nearly (0, 0.80) meaning that the prior probability mass is mainly concentrated in this interval. However, one can argue that this is an unnecessary wide prior interval for the toxicity probability on this combination. Specifically, there is no need to model this toxicity probability as, say, more than 50%, if the target toxicity is γ = 0.30 as such combination would not be chosen anyway due to the safety concerns. There is a similar argument for p ₃₃, but for low toxicity probability values. There is no need to consider the prior probability interval having a considerable mass below, say 15%, as the highest combination would be recommended in any case. Note that the choices of the values 50% and 15% are arbitrary in our example and should be defined with clinicians in an actual trial. While the choice of c = 25 is very restrictive and does not satisfy arguments above, the moderate choice (e.g. c = 4) still implies a large variability on probability estimates which is enough for the purposes of Phase I trials. Indeed, it was found that the use of more informative prior distributions (e.g. c = 4 against c = 1) prevents the unstability of the proposed surface-free design (see the Supplementary Materials). Motivated by these findings, we choose c = 4 for the illustration of the dose-escalation. Finally, as mentioned above, the proposed parameterisation implies a higher variance at higher combinations. For example, fitting the Beta distribution for p ₃₃ with the same mean and variance as implied by the proposed parameterisation, one can find that the corresponding effective sample size is nearly c = 3 which is lower than for the lowest combination (c = 4). This means that the model implies more uncertainty at the higher combinations than at the lower ones. The escalation algorithm in the individual trial is given in the following section.

3.4. Individual trial escalation

For illustration, we study the behaviour of the design in one scenario given in Table 1.

Table 1. Illustration combination-toxicity scenario.

Drug B	Drug A
	A1	A2	A3
B1	.02	.05	.12
B2	.10	.20	.30
B3	.15	.30	.50

Note: The MTCs are in bold. MTC: Maximum tolerated combination.

There were several escalation restrictions imposed by clinicians, which we also adapted here. Specifically, the trial is restricted to start from the lowest combination (A ₁, B ₁) and combination skipping and “diagonal” escalation is not allowed. Then, the design assigns the next cohort of patients to the combination with the estimated toxicity probability closest to the target subject to these constraints.

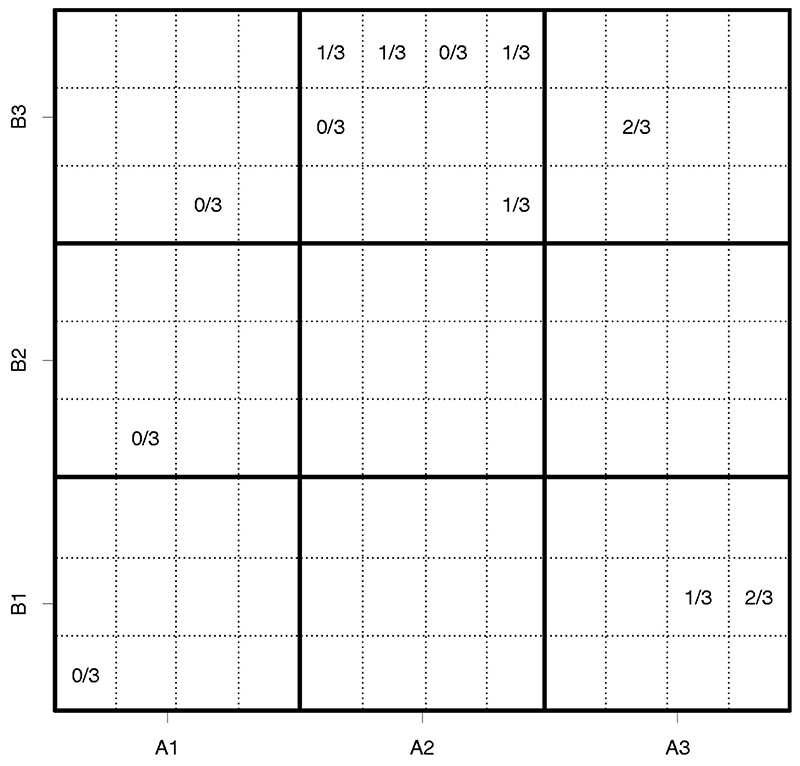
The cohort allocation in one individual trial is given in Figure 3. Large cells (in bold frames) correspond to the combinations as in Figure 1. Each cell is divided into twelve sub-cells corresponding to 12 cohorts to be assigned in the study. Then, if a particular combination has been given to a cohort, the corresponding cell contains the number of toxicity outcomes observed (Fout of 3) for this cohort.

Figure 3. Allocation of 12 cohorts to combinations in the individual trial.

As restricted, the trial starts from combination (A ₁, B ₁). Once no toxicities were observed, the design escalates the amount of B. Similarly, after no toxic responses, the design escalates the amount of the compound B further. Since there is no toxic response observed for cohort 3, the next cohort receives the same amount of drug B and escalated the dose of drug A. As there is one toxic response observed for cohort 4, the next cohort is still allocated to the same combination. After no toxic responses for cohort 5 given combination (A ₂, B ₃), the design escalates the amount of drug B further. Given two toxic outcomes, the design allocates cohort 7 to combination (A ₃, B ₁), so the amount of drug B is escalated. As there is one toxic response, the design allocated cohort 8 to the same combination. Further, after two toxic responses, the design moves to the anti-diagonal combination (A ₂, B ₃) which is the MTC. All further patients are allocated to it and it is recommended as the MTC in the trial. Importantly, while there are two MTCs, in this individual trial, another MTC is not visited due to the selected allocation rule – assign the next patient to the estimated MTC. Once the MTC is found, the design is unlikely to switch to other combinations. However, in many replications of this trial given below, we will see that both combinations are visited and selected.

Overall, the proposed design selected the correct MTC and all escalation/de-escalation steps are ethical, intuitive and in line with general clinical principles. As only one possible outcome is considered above, we study the performance of the proposed design using many simulated trials below.

3.5. Replicated trials

Here we consider the performance of the design in 2000 replicated trials. To simplify the presentation we consider four groups of combinations, specifically, low combinations: (A ₁, B ₁), (A ₂, B ₁), (A ₁, B ₂) located in the beginning for the combinations grid and corresponding to the toxicity probability of no more than 10%; medium combinations: (A ₃, B ₁), (A ₂, B ₂), (A ₁, B ₃) located in the middle of the grid and having toxicity probability of 12–20%; MTCs: (A ₃, B ₂), (A ₂, B ₃) corresponding to the target toxicity probability of 30%; and the high combination: (A ₃, B ₃), the unsafe combination with the toxicity probability of 50%, far beyond the target one. Software in the form of R code implementing the proposed design for the settings with three doses (Section 3) and four doses (Section 4) of both agents, as well as a procedure to derive the prior distribution parameters is available at github.com/ dose-finding/surface-free-design.

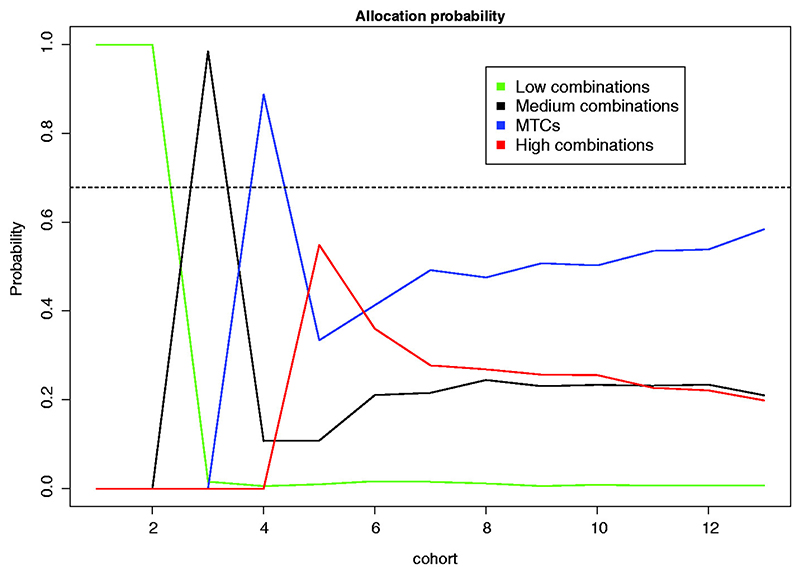
The probability of each cohort to be allocated to each of these groups is given in Figure 4. The allocation probability for cohort 13 corresponds to the proportion of each group selections as the MTC. The performance of the design is also compared with the non-parametric optimal benchmark.^23,24

Figure 4.

Allocation probabilities of 12 cohorts to combinations in 2000 replicated trials. The allocation probability for cohort 13 corresponds to the proportion of each group selection as the MTC. The dashed horizontal line corresponds to the proportion of correct selections for the non-parametric optimal benchmark.

Due to constraints of the trial, the first two cohorts are assigned to low combinations with probability 1. Further, as the toxicity probabilities for these doses are low, the design escalates with probability close to 1. Cohort 3 is then assigned to medium doses, which have a lower than 0.30 toxicity probability. Consequently, the cohort 4 would be escalated further to MTCs combination. As cohort 4 can experience several MTC with non-neglected probability, the design might de-escalate to medium combinations or stay at one of the MTCs for cohort 5. Alternatively, if no toxicities are observed (which is more likely given that the toxicity probability at the current combination is 30%), it escalates further which corresponds to an increase in the allocation probability for the high combinations (red line). However, for cohort 6, the probability of patients being allocated to the highly toxic combinations drops while the probability to be allocated to the MTC or the medium combinations increases. The allocation probability for the MTCs stabilises after cohort 6 and the probability of being allocated to one of the true MTCs increases as the trial progresses. Overall, the design selects one of the correct MTC in 58.4% of the trials with each combination selecting in 28.4% and 30% of trials. This performance is close to the performance of the optimal non-parametric benchmark – 67.8%. This makes the performance of the proposed design promising and a further investigation in many different scenarios is provided below.

4. Simulations

4.1. Setting

In this section, we study the performance of the proposed surface-free design in a number of different scenarios. Similar to the setting considered in the original paper proposing another model-free design, PIPE,⁷ we consider m = 4 × 4 = 16 combinations, N = 50 patients, and cohort size 1. The dose–toxicity relation is known to be monotonic within each agent and, therefore, the proposed design can be applied. The goal of the study to find the MTC corresponding to c = 0.20. A clinician considers a selection of a combination with toxicity probability in the interval (0.10, 0.30) as an acceptable one. We focus on (i) the proportion of correct MTC selections, (ii) the proportion of acceptable selections, (iii) the mean number of toxic outcomes in one trial and (iv) the mean number of patients assigned to the MTC.

As the performance of the novel design and other competitive designs (described below) is expected to depend on the simulation scenarios selected for the evalution,²⁴ we consider a large number of scenarios studied in the literature. Specifically, we consider scenarios studied in the PIPE paper,⁷ two scenarios used in the POCRM paper⁶ in the setting with four dose levels of both agents, and 14 scenarios considered by Riviere et al.²⁵ but adapted for 20% target toxicity and the setting with four dose levels. Below, we will focus on 10 of these scenarios only and present the complete results in the Supplementary Materials. The scenarios are given in Table 2.

Table 2. Ten considered combination-toxicity scenarios.

Drug A						Drug A
Sc 1	Drug B	A1	A2	A3	A4	Sc 6	Drug B	A1	A2	A3	A4
	B1	.02	.04	.06	.08		B1	.04	.05	.07	.10
	B2	.05	.07	.09	.11		B2	.07	.08	.20	.30
	B3	.08	.10	.12	.14		B3	.10	.20	.33	.40
	B4	.11	.13	.15	.17		B4	.33	.37	.40	.47
					Drug A						Drug A
Sc 2	Drug B	A1	A2	A3	A4	Sc 7	Drug B	A1	A2	A3	A4
	B1	.10	.20	.30	.40		B1	.05	.08	.11	.12
	B2	.25	.35	.45	.55		B2	.07	.10	.20	.30
	B3	.40	.50	.60	.70		B3	.08	.20	.33	.37
	B4	.55	.65	.75	.85		B4	.20	.33	.37	.40
					Drug A						Drug A
Sc 3	Drug B	A1	a2	A3	A4	Sc 8	Drug B	A1	A2	A3	A4
	B1	.44	.48	.52	.56		B1	.03	.05	.07	.09
	B2	.50	.54	.58	.62		B2	.06	.08	.10	.20
	B3	.56	.60	.64	.68		B3	.10	.20	.30	.33
	B4	.62	.66	.70	.74		B4	.30	.33	.40	.47
					Drug A						Drug A
Sc 4	Drug B	A1	A2	A3	A4	Sc 9	Drug B	A1	A2	A3	A4
	B1	.12	.13	.14	.15		B1	.05	.07	.10	.20
	B2	.16	.18	.20	.22		B2	.10	.20	.30	.35
	B3	.44	.45	.46	.47		B3	.20	.33	.40	.43
	B4	.50	.52	.54	.55		B4	.30	.40	.47	.50
					Drug A						Drug A
Sc 5	Drug B	A1	A2	A3	A4	Sc 10	Drug B	A1	A2	A3	A4
	B1	.01	.02	.03	.04		B1	.03	.08	.13	.20
	B2	.04	.10	.15	.20		B2	.07	.13	.20	.27
	B3	.06	.15	.30	.45		B3	.20	.28	.35	.41
	B4	.10	.30	.50	.80		B4	.30	.33	.40	.47

Note: The MTC is in bold and acceptable combinations are underlined. MTC: Maximum tolerated combination.

The 10 scenarios are selected such that a large variety of possible combination-toxicity scenarios in which the MTC can be located at lower, moderate or high combinations is covered. Scenario 3 corresponds to a highly toxic scenario in which none of the combinations should be recommended. The chosen scenarios also allow to investigate the performance of the design for different interaction mechanisms between compounds. For instance, scenarios 8–10 represent cases in which the interaction independence assumption is clearly violated.

4.2. Design specification

The proposed design requires prior distribution for all ratios to be specified. As there are four dose levels of each compounds, this results in seven ratios in the design. Following the reasoning above, we select the strength of prior for each connection to be c ₁ = … = c ₄ = t ₂ = … = t ₄ = 4. As it can be challenging to compare designs with different prior distributions, we aim to match the prior point estimates for the PIPE design as used in the original work.⁷ For this, we fix a ₁ = … = a ₄ e ₂ = … = e ₄ ≈ 3.81 resulting in the following prior point estimates at all 16 combinations.

$$P(0)=\left[\begin{array}{cccc}0.05& 0.10& 0.15& 0.19\\ 0.10& 0.15& 0.19& 0.23\\ 0.15& 0.19& 0.23& 0.27\\ 0.19& 0.23& 0.27& 0.30\end{array}\right]$$

Note that although the prior point estimates for PIPE and the proposed design are nearly matched, the proposed design and PIPE will use different strength of prior distributions of toxicity probability at each combination. For the proposed design, the selected strength of prior could be considered as an “operational prior”, the prior that is found to provide good operating characteristics in many different scenarios. As it was argued by Cheung¹⁹ that the strength of the prior is of a crucial importance in model-free dose-finding, we study the robustness of the proposed design for various value c, the strength of prior, and fixed prior point probability estimates in the Supplementary Materials. Specifically, it is found that the propose design performs similarly for moderate values of c ∈ (3, 6), and is not sensitive to its choice in this range.

The toxicity threshold of the safety constraint (9) is fixed to be equal to the target probability γ = γ*. The overdosing probability threshold ξ = 0.7 is chosen corresponding to a conservative safety constraint. We will refer to the surface-free design as “SFD”.

We compare the performance of the novel design to two designs, a model-free PIPE design, and model-based POCRM design. The PIPE design is chosen for the comparison as it provides an alternative approach to a model-free dose-finding (as the proposed approach), and the POCRM design is chosen as it was found to result in better performance (on average) than other dose-finding designs.¹² The PIPE design⁷ which does not use any parametric assumption between doses and considers all possible monotonic “contours”. The design is specified as in the original proposal and pipe.design package²⁶ in R²⁷ is used for simulations. We also compare the performance to the maximum likelihood version of the model-based CRM design for partial ordering (POCRM).⁶ We use the pocrm package²⁸ in R for the simulation. Note that POCRM design does not require specification of prior distributions but the initial escalation rule (until one toxicity and one non-toxicity are observed). All the parameters and initial escalation phase are fixed as proposed in the original work. We specify six orderings between which the POCRM random!odification is the safety constraint which is not originally included in the package. We adopt the following safety constraint. Once the estimate of the parameter β is obtained, we compute the variance of the estimator.²⁹ Then, we employ the delta-method and the normal approximation of the toxicity at the first combination with corresponding mean and variance to compute the probability that the toxicity is above γ*. If this probability is higher than 0.8, the trial is terminated.

4.3. Operating characteristics

The summary statistics, the proportions of the MTC selections and acceptable combinations selections are given in Figure 5, and the proportion of each combination selection is given in the Supplementary Materials.

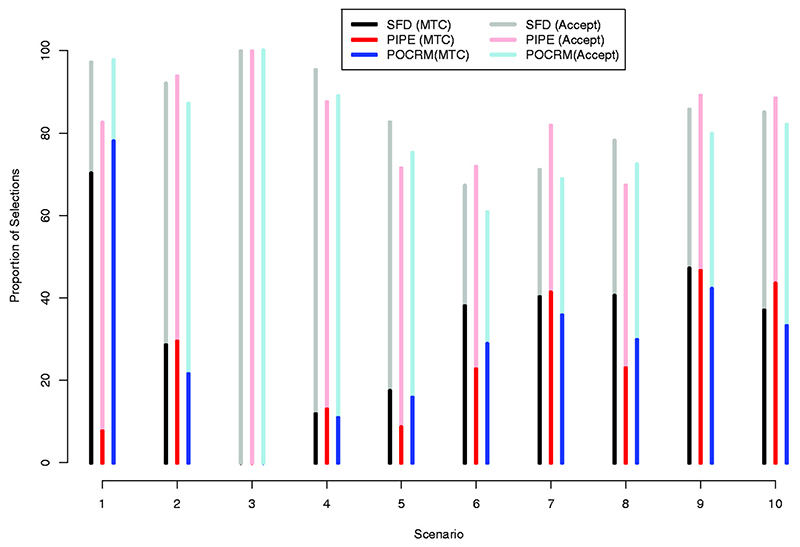
Figure 5.

Proportions of MTC selections (bright colours) and acceptable combination selections (transparent colours) in scenarios 1–10 by the Surface-Free Design, SFD (black), the PIPE design (red) and by the POCRM design (blue). Results are based on 2000 simulations.

Considering the proportion of MTC selections, SFD performs similarly to one of the competing designs and better than another in more than half of scenarios: 2, 5–7 and 9–10. For instance, in scenario 2, SFD performs comparably to PIPE and outperform POCRM by 10%, and, in scenario 6, SFD performs comparably to POCRM and outcomes PIPE by 10%. The novel design outperforms both alternatives in scenario 8 by 13–16% and performs similarly to them in scenario 4. The only scenario in which SFD is outperformed by one of the competing designs is scenario 1. In this scenario, the highest combination is the MTC and POCRM benefits from the model-based nature resulting in 80% of correct selections compared to 71% by SFD. This, however, is still remarkably higher than for PIPE design – 8% of correct selections. SFD also shows the robust performance in scenarios 6–10 with different interaction structure: it results in 40–47% of correct selections across all of these scenarios. Comparing the average performance, the average proportion of MTC selection across all scenarios is 33% for the proposed SFD design and 24% for PIPE and 30% for POCRM.

Regarding the proportion of acceptable selections, SFD recommends the combination with toxicity probability between 0.10 and 0.30 in at least 80% of trials in scenarios 1–5 and 8–9 and in nearly 70% of trials in scenarios 6– 7. The only scenario in which SFD is outperformed by at least one competitive method by more than 5% is scenario 7: SFD recommends the acceptable combination in 72% of trials comparing to 82% by PIPE. At the same time, one can find a scenario in which the proportion of acceptable selections is greater for SFD, e.g. in scenarios 1, 5 and 8. POCRM leads to the best proportion of acceptable selections in flat scenario 1 – as well as SFD. At the same time, it recommends the acceptable combination less often than SFD and PIPE in toxic scenario 2. Again, comparing the average performance, the average proportion of acceptable selections across all scenarios is 85% for the proposed SFD design and is 83% for PIPE and 81% for POCRM. Consequently, the proposed design results in higher proportions of both the MTC and acceptable selections under the considered scenarios than the alternative approaches, on average.

The summary statistic and the mean number of toxic responses illustrating the safety properties of the designs are given in Table 3, while the experimentation proportions (the proportion of patients assigned to each combination) for each combination are given in the Supplementary Materials.

Table 3. Operating characteristics of SFD, PIPE and POCRM design in scenarios 1–10.

	Sc.1	S.2	Sc3	Sc4	Sc5	S.6	Sc.7	Sc.8	Sc.9	Sc.10
Mean number of toxic responses
SFD	7.2	12.3	5.0	10.6	9.9	10.6	10.6	10.3	11.4	11.3
PIPE	6.6	14.3	4.8	11.7	7.9	9.8	9.8	9.2	11.3	11.1
POCRM	6.a	12.1	8.3	10.5	9.9	10.3	10.2	10.1	10.6	10.6
Mean number of patients on the MTC
SFD	26.4	10.8	–	5.3	6.9	12.9	15.9	14.1	17.6	14.9
PIPE	8.4	9.5	–	6.2	7.1	12.0	17.4	13.2	19.3	17.3
POCRM	28.0	7.5	–	4.9	5.2	9.5	12.5	9.5	15.5	12.5

Note: Results are based on 2000 simulations. MTC: maximum tolerated combination; SFD: surface-free design; PIPE: product of independent beta; POCRM; partial ordering continual reassessment methods.

All considered designs are able to terminate the trial in the highly toxic scenario 3 in 99% of trials. However, POCRM requires more patients to come to the same conclusion which results in nearly three more toxic outcomes on average. POCRM results in a fewer number of toxic responses in the majority of other scenarios: 1–2, 4–6, and 9–10. PIPE results in a greater number of toxicities in scenarios 2 and 6 (2 excessive toxic outcomes) and in scenario 4 (one excessive toxic outcomes) comparing to other methods. The difference in the average numbers of toxic responses for SFD and any the competitive design in each scenario does not exceed 1 DLT. Finally, the design performs similarly in terms of the proportion of patients assigned to the MTC with a difference of no more than three patients.

Overall, the proposed SFD design finds the MTC with a high probability and outperforms at least one of the competitive methods in the majority of scenarios while performing similarly to another alternative. The proposed method also results in the same or greater proportion of acceptable selection and leads to not more than one excessive toxic response in the considered scenarios.

5. Discussion

In this work, the extension of the curve-free design¹⁷ is proposed. The major advantage of the proposed design is that (i) it does not require any parametric assumption on the combination-toxicity surface (and, therefore, is called a surface-free approach) and can fit a large variety of combination-toxicity shapes and (ii) it does not require any particular orderings to be specified prior to a trial. It was found in the simulation study that the proposed design performs comparably or better than methods currently used in practice with no cost in terms of toxic responses. Importantly, PIPE design has the same non-parametric nature, but it parameterises the probability of toxicity at each dose level separately. It is found that parameterising the connection between toxicity probabilities can be more beneficial and lead to higher proportions of correct selections.

It is important to mention that the interaction between compounds plays a crucial role in combination studies. However, following the recent findings that the estimation of additional parameters associated with interaction does not bring any benefits in the selection of the target combination due to limited sample size in Phase I,¹⁸ the novel design uses the drugs interaction independence assumption to simplify the estimation problem. Importantly, it does not prevent it from finding the MTC in scenarios with this assumption violated and leads to good operating characteristics compared to other currently used designs. At the same time, due to the no-interaction assumption, the prior for the design might not be matched exactly to a given approach that should be considered when comparing the proposed approach to other alternatives. Furthermore, the designs, indeed, requires a number of parameters to be estimated. Again, this does not prevent the approach from finding the MTC with high probability while keeping the flexibility in modeling the combination-toxicity relationship.

The performance of the proposed approach depends on the chosen prior distribution, and, specifically, on the strength of the prior distribution imposed on the connections. We have provided a guideline on how the strength of prior can be chosen in the settings of dual-agent trials with 3 and 4 doses for each agent. When applying the method to other settings, the calibration of this parameter should be performed using the arguments of how vague the underlying distribution is (as in Section 3) and the sensitivity analysis to various values of c in the simulation scenarios (as in the Supplementary Materials).

While the construction proposed in this work starts from the parametrisation of all connections and subsequent elimination of the redundant ones, one can observe that the proposed parametrisation can be also obtained using two marginal curve-free models¹⁷ under the no-interaction assumption. Specifically, under the no-interaction assumption the probability on toxicity of combination (i, j) can be written as

$$p_{ij}=1-\left(1-p_i\right)\left(1-q_j\right)$$ (10)

where p_i is the probability of toxicity given dose d_i of agent A and q_j is the probability of toxicity given dose d_j of agent B. Using the curve-free parametrisation given in Section 2.1, the marginal probabilities can be written as p_i = 1 − δ ₁,…, δ_i and q_j = 1 − τ ₁,…, τ_j. Plugging in the probabilities into equation (10), one can find that the probability of toxicity given the combination (i, j) under no-interaction assumption can be written as p_ij = 1 − δ ₁…δ_iτ ₁…τ_j. Specifically, the probability for the first combination (1,1) can be written p ₁₁ = 1 − δ ₁ s ₁. However, this model implies that p ₁₁ is both an estimate of the first compound and the second compound. Therefore, the model above is not identifiable. To overcome this, one can reparametrise δ : δ ₁ τ ₁. Then, the probability of toxicity given the combination (i, j) under this construction is equivalent to the parametrisation given in equation (6). Despite the equivalence of the final statistical model, the parametrisation as given in Section 2.2 is chosen as it allows to demonstrate implications of the no-interaction assumptions, and, if needed, it allows to construct the model including the interaction of compounds.

Interestingly, it was found³⁰ that unless one is dealing with informative prior information, the curve-free design coincides with the model-based CRM: whatever choices (of prior distributions) are made for one method, there exist choices for the other method, such that the operating characteristics of both methods are the same. While the POCRM⁶ being a natural extension of the original CRM design requires the set of toxicity orderings to be specified, the dual-agent extension of the curve-free design proposed in this work does not require any orderings, and therefore can be preferable to avoid randomisation between orderings in Phase I clinical trials.

While the proposed design was applied to the case of the dual drug combination, it can be straightforwardly generalised to three and more combinations. Following the similar concept of parametrising ratios and using the independence assumption, one can apply the novel design to a wide range of studies. At the same time, the extension of the proposed design to a clinical trial investigating the combinations of molecularly targeted agents can be of great interest. The distinguishing feature of such a trial is a possible plateau in the dose–toxicity relation. In this case, the ratio between doses in the plateau is equal to 1 and this possibility needs to be modelled independently. Additionally, the application of the proposed design to Phase I/II clinical trials that evaluate jointly toxicity and efficacy endpoints is a subject for further investigation.