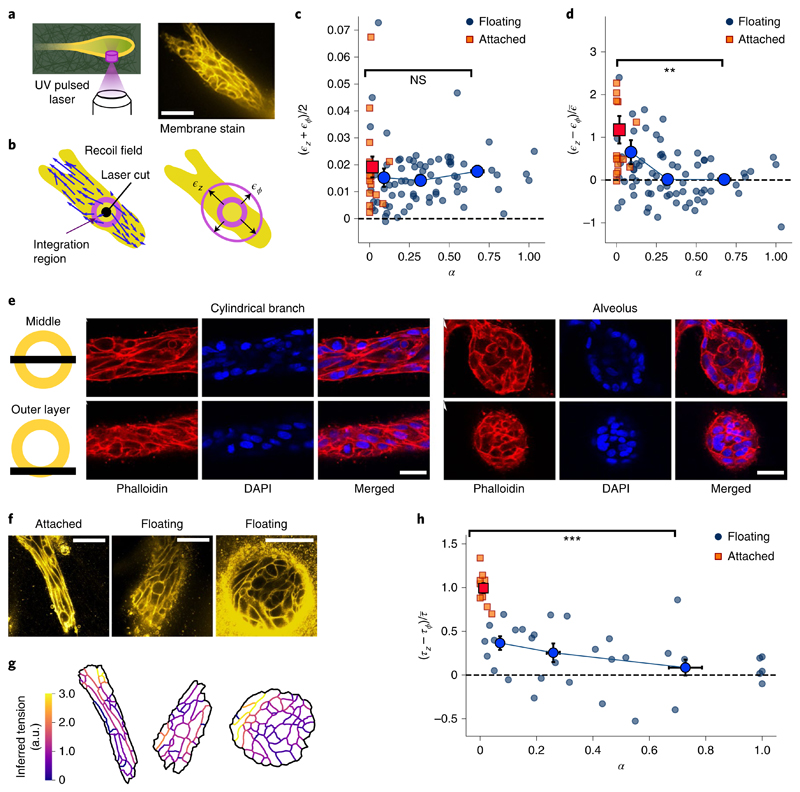
Fig. 2. Alveoli are under isotropic tension and cylindrical branches are under axially biased tension.

a, We ablate a cylindrical region with a diameter of 10 μm and height of 30 μm, cutting through the ECM and the outer cell layer. From the recoil, we estimate the axial and circumferential elastic strains. Scale bar, 50 μm. b, Displacement field induced by the cut. We integrate the optical flow over an annular region to obtain the recoil strains. c, Mean recoil (ϵ_z+ϵ_ϕ)/2 as a function of shape index α, both in attached (n = 16) and floating (n = 73) gels. d, Recoil anisotropy (ϵ_z – ϵ_ϕ) as a function of shape index α for the same experiments as in c (P value, 8 × 10⁻⁴). To compare with the force inference data in h, we scaled by the mean recoil averaged over the whole dataset, namely, $\overline{\epsilon }=0.017.$ e, Confocal microscopy of actin and nuclei in a cylindrical branch and a spherical alveolus. Top: slice through the middle plane. Bottom: slice through the outer cell layer. f, Cell membrane stains. Scale bars, 50 μm. g, From the membrane segmentations, we computed the tensions using the curvilinear-boundary force inference method. h, Inferred tension anisotropy (τ_z–τ_ϕ) as a function of shape index α, both in attached (n = 10) and floating (n = 32) gels (P value, 2 × 10⁻⁷). Note that we assume $\overline{\tau }=1.$ NS, not significant; **P < 0.010; ***P < 0.001.