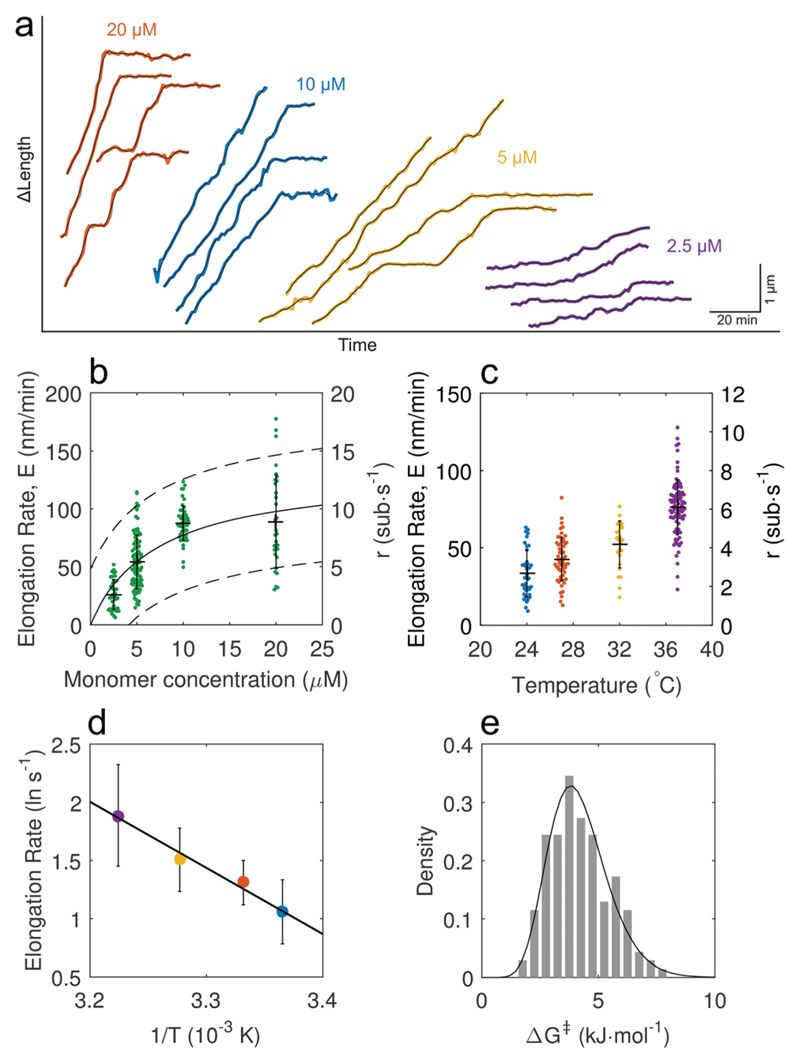
Fig. 2. A quantitative analysis of single Aβ42 fibril elongation assays allows the extraction of kinetic parameters.

(a) Examples of length traces obtained from fast growing fibril ends. The elongation rate dependence on monomer concentration is clearly visible, (b) the rate of pause-free elongation has a linear concentration dependence initially and saturates at high monomer concentration. Fitting the data points to a Michaelis–Menten model yields the solid line; broken lines indicate the 95% confidence bounds of the non-linear fit (error bars denote mean ± S.D.). m_1/2 = 7.2 ± 2.4 μM, maximum elongation rate E_max = 133 ± 20 nm min⁻¹. Data points were combined from two independent repeats. N = 25, 40, 40, 18 for 2.5, 5, 10, 20 μM respectively. (c) Temperature dependence of the elongation rate at the fast end (error bars denote mean ± S.D.). N = 18, 33, 13, 32 for 24 to 37 °C at 10 μM monomer concentration. (d) The temperature dependence of the fast end elongation rate shows Arrhenius behaviour and a linear fit yields the enthalpy of activation ΔH^‡ = 47 ± 17 kJ mol⁻¹ (R² = 0.987, ±95% CI). Error bars denote the mean ± S.D. from fits of normal distributions to the CDFs. (e) Free energy of activation ΔG^‡ distribution for an ensemble of fibrils calculated from elongation rates obtained for monomer concentrations below 10 μM.