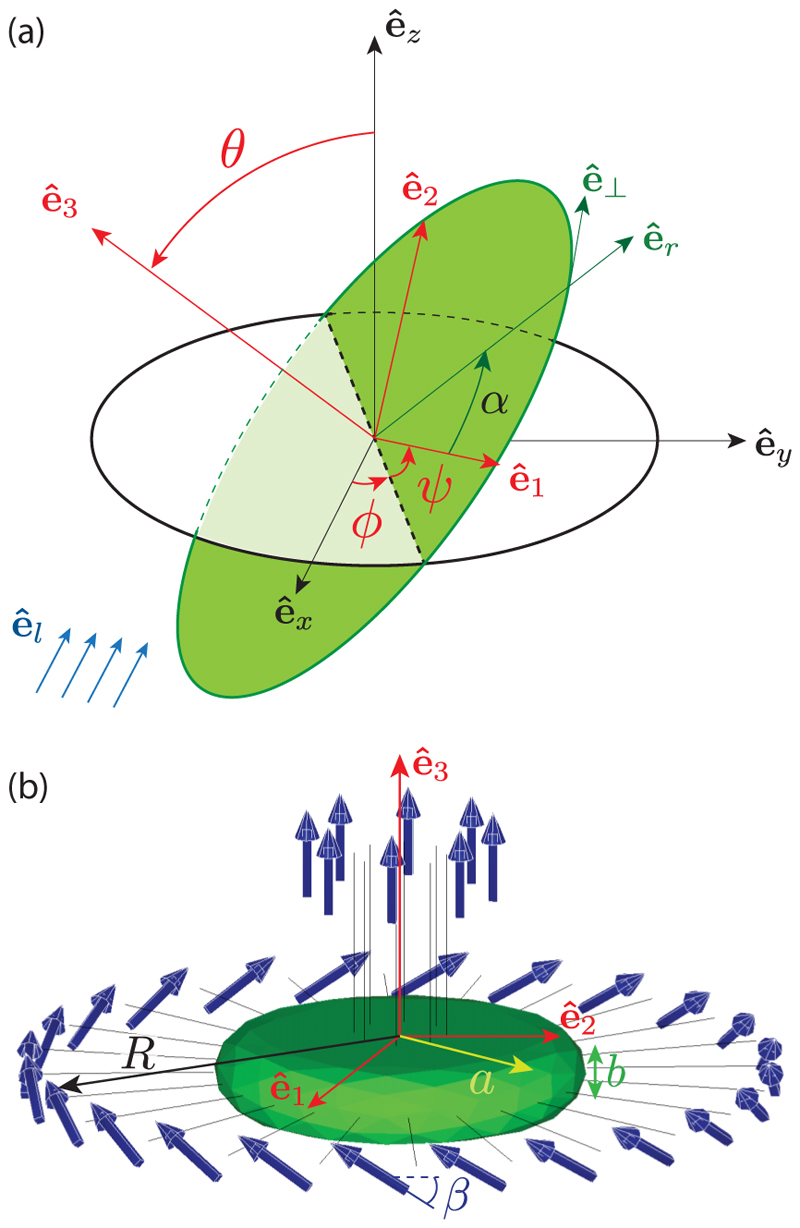
Fig. 4. Details of computational geometry.

(a) Coordinates system and Euler angles. The frame (ê_x, ê_y, ê_z) is attached to the laboratory; the frame (ê₁, ê₂, ê₃) is attached to the Gonium body (green disk), with ê₃ the symmetry axis and (ê₁, ê₂) in the body plane. Euler angles (θ, ϕ, ψ) relate the two frames: by definition, θ is the angle between ê_z and ê₃, ϕ is the angle from ê_x to the line of nodes (dotted line), and ψ is the angle from the line of nodes to ê₁. In the Gonium body plane (ê₁, ê₂), the flagella are labeled by the angle α, with (ê_r, ê_⊥) the corresponding local frame such that cos α = ê₁ · ê_r. For the computation of the phototactic response, we assume the light is incident along ê_l = − ê_x (blue arrows). (b) Gonium geometry for simulations. The body (in green) is a thick disk with radius a = 20 µm and thickness b = 8 µm. Flagella (length 20 µm) associated with a point force 20 µm away from the cell body are attached to the body. The 8 central flagella generate thrust while the 24 peripheral ones are tilted by β ≃ 30° and generate both thrust and rotation.