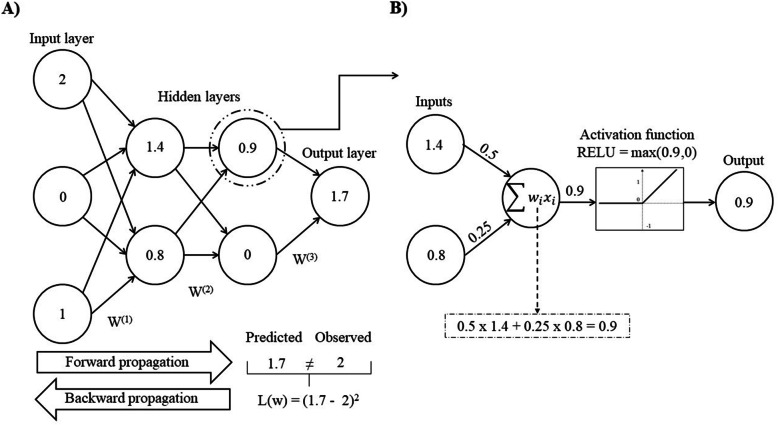
Fig. 4.

Representation of a Multilayer Perceptron (MLPs) architecture. In (a) The structure of the deep neural network (DNN) and the training process including forward and backward propagation are depicted. In the forward propagation information flows from the input to the output layers by outputting the calculations of the activation function to the next layer. In the backward propagation, the output is assessed and a loss function L(W) [i.e. mean square error] is used to minimize the overall error function, and consequently update the network weights using stochastic gradient descent. In (b) The underlying calculations for each unit in order to provide the output to the next layer. In this process, weight vectors [W^(.)] and inputs are linearly combined and transformed based on an activation function, i.e., rectified linear which outputs the maximum between zero and the linear combination of weights and inputs. This figure is based and adapted from the diagram proposed by Angermueller et al. (2016) [44]