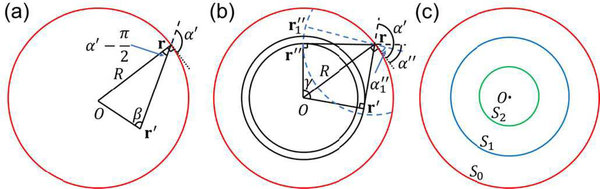
Fig. 1.

Analysis of the spatial aliasing for a circular geometry. (a) A full-ring transducer array of radius R (red circle), where a detection element location r and a source point location r′ are marked. The locations r and r′ are also seen as vectors from the origin to these locations. Vectors -r′ and r−r′ form an angle β, while the extension of line segment r−r′ forms an angle α′ with the tangential dotted line that is perpendicular to r. The angle formed by vectors −r and r′−r can be expressed as ${\alpha }^{\prime }-\frac{\pi }{2}$. This graph is used to analyze the aliasing in SS. (b) A full-ring transducer array with a detection element location r, two reconstruction locations r″ and ${\mathbf{r}}_1^{″}$ and a source point location r′ marked. Extensions of the line segments r−r″, $\mathbf{r}-{\mathbf{r}}_1^{″}$ and r′−r can be expressed as α″, ${\alpha }_1^{″}$ and α′, respectively, with the tangential dotted line that is perpendicular to r. Vectors r″ and r′ form an angle $\gamma =\arccos \left(\frac{r^{″}}{R}\right)+\arccos \left(\frac{r^{\prime }}{R}\right)$ where r″ = ‖r″‖. Points r″ and ${\mathbf{r}}_1^{″}$ are on the same circle centered at r. This graph is used to analyze aliasing in IR. (c) Regions in the field of view representing different types of aliasing. In S₂ (green circle), which contains all source points and reconstruction locations, UBP reconstruction yields no aliasing. In S₁ (blue circle), aliasing does not exist in SS but may exist in UBP reconstruction. In S₀ (red circle), aliasing may exist in SS.