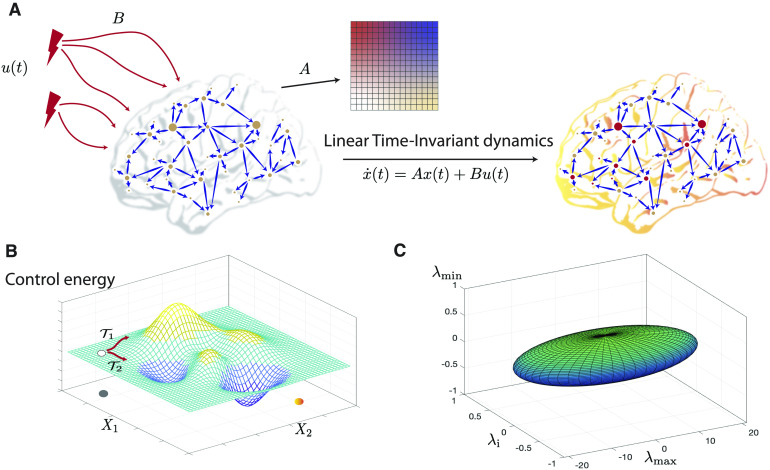
Figure 3. .

Control theory applied to brain networks. Control theory seeks to determine and quantify the controllability and observability properties of a given system. A system is controllable when a control input u(t) is guaranteed to exist to navigate the system from a given initial state to a desired final state in a specified span of time. (A) We begin by encoding a brain network in the adjacency matrix denoted by A. Then, control signals u(t) act on the network via the input matrix B, leading to the evolution of the system’s state to a desired final state according to some dynamics. The most common dynamics studied in this context is a linear time-invariant dynamics. Whether the system can be navigated between two arbitrary states in a given time period is determined by a full-rank condition on the controllability matrix. (B) The control energy landscape dictates the availability and difficulty of transitions between distinct system states. For a controllable system, several trajectories can exist which connect the initial and final states. An optimum trajectory is then determined using the notion of optimal control. (C) The eigenvalues of the inverse Gramian matrix quantify the ease of moving the system along eigen directions that span the state space and form an N − ellipsoid whose surface reflects the control energy to make unit changes in the state of the system along the corresponding eigen direction. Here we show an ellipsoid constructed from the maximum, the minimum, and an intermediate eigenvalue of the Gramian for an example regular graph with N = 400 nodes and degree l = 40. The initial state has been taken to be at the origin, and the final state is a random vector of length N with unit norm. Commonly used metrics of controllability such as the average controllability, can be constructed from the eigenvalues of the Gramian.