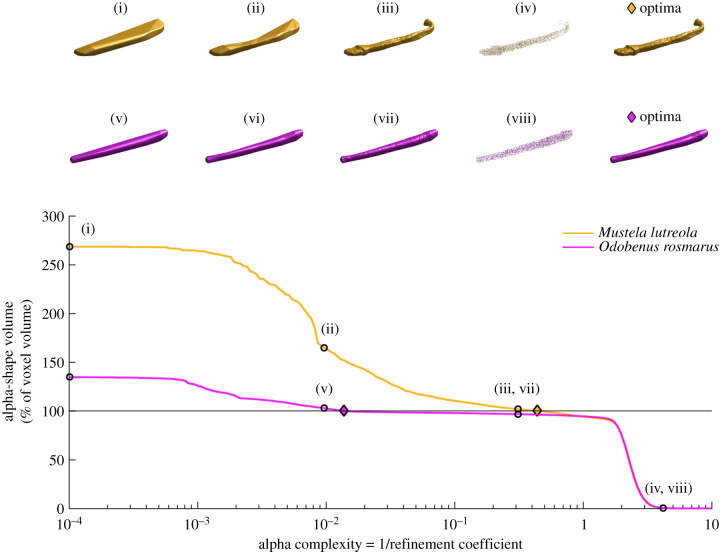
Figure 1.

The alpha shape protocol for estimation of three-dimensional shape complexity. As the alpha complexity is increased (left to right on the x-axis), the alpha shape fitted to the underlying CT data becomes increasingly refined. Alpha complexity is defined as the inverse of Gardiner et al.'s [13] refinement coefficient, such that increasing shape complexity is represented by increasing values. The alpha complexity necessary in order for the volume of the alpha shape to match that of the CT dataset (100% on the y-axis) is reported as the ‘optimal' alpha complexity. An outwardly ‘simple' baculum (walrus, Odobenus rosmarus) rapidly converges on optimal alpha complexity at relatively coarse level of refinement coefficient (purple diamond; inset v–viii). By contrast, a seemingly more ‘complex' baculum (European mink, Mustela lutreola) requires a much more refined alpha shape fit (yellow diamond; inset i–iv) in order for the model volumes to converge. Beyond this point, at very high levels of alpha complexity, alpha shapes begin to break down and no longer form one contiguous shape. At this stage, alpha shape volumes become less than the volume of the original mesh. A more detailed description of the alpha shape methodology is available elsewhere [13]. (Online version in colour.)