Figure 1.

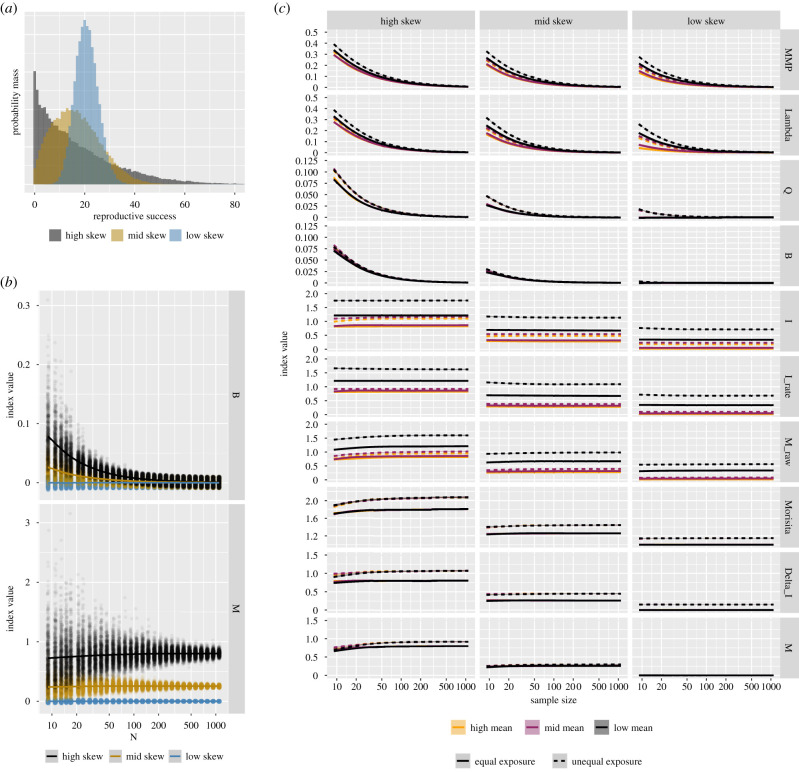
We analyse 270 000 simulated RS datasets to illustrate the effects of sample size (30 different levels), mean RS (three different levels), unequal exposure time (two different levels), and reproductive skew (three different levels) on 10 indices of reproductive skew. We consider three levels of skew for each combination of the other variables, and use 500 replicates per category combination to estimate a mean index value. In frame (a) we show the shape of three example Negative Binomial distributions from which RS realizations are drawn. Mean RS is constant across the plotted skew categories. In the high skew category (black), there is elevated probability mass on both low and high RS values, relative to the low skew category (blue). In the full simulation, we set the exponent of a rate scaling random effect (0.01 = low skew, 0.31 = mid skew, and 0.61 = high skew) to modulate skew as illustrated here. The mean of the Negative Binomial distribution was defined using a rate per exposure time unit of 1.0 = low, 7.0 = mid, and 20.0 = high. Sample size is modulated by randomly drawing n samples from each distribution. We then calculate each skew index using the n-vector of sample RS outcomes. We also consider the effect of variation in exposure time, with Equal Exposure time resulting from use of equal and fixed exposure times, and Unequal Exposure resulting from drawing exposure times from a uniform distribution. Frame (b) gives an example contrast between B and M. Mean RS is held constant within this frame. For each level of skew (low = blue, mid = yellow, high = black), we draw a random sample of n RS outcomes and then calculate M and B on this vector of simulated data. We repeat this process 500 times for each considered value of n and plot the results. The solid lines indicate average values. We see that—holding constant both mean RS and reproductive skew—B is highly sensitive to sample size. For large samples, B is actually insensitive to reproductive skew, and goes to zero regardless of the actual level of reproductive skew in the generative model; there is a structural bias in its mathematical definition. In contrast, M is sensitive to skew differences and is invariant to sample size. As sample size increases, M can cleanly differentiate between skew levels. We repeat this same analysis in frame (c) for all other combinations of variables and skew indices, but we plot only the mean trends. Specifically, we plot ‘Maximum mating proportion’ (MMP), λ, Q, B, I, I of RS rate, $\check{M}$, Morisita’s $I_{\sigma }$, Waples’ Δ_I, and M as a function of sample size. The x-axis is plotted with log-transformed values, but labelled in natural units. Within each frame, the skew level is fixed. Colours are used to illustrate the effect of mean RS. Line-type is used to illustrate the effect of exposure time differences. A useful comparative measure of skew will: (i) be invariant to sample size (i.e. we should see flat horizontal lines within frames), (ii) be invariant to mean RS and exposure time changes (i.e. all lines should overlap within each frame), and (iii) be sensitive to skew (i.e. the y-axis locations of the lines should vary across columns). We observe: (1) MMP and λ are sensitive to sample size, mean RS, and exposure time; (2) Q is invariant to mean RS, but not exposure time or sample size; (3) B is invariant to exposure time and mean RS, but varies sharply as a function of sample size; (4) while I and I of RS rate are invariant to sample size and can distinguish between levels of skew, they are sensitive to mean RS; (5) $\check{M}$, like I, is invariant to sample size, and can distinguish between levels of skew. It, however, remains sensitive to mean RS; (6) Morisita’s $I_{\sigma }$ and Waples’ Δ_I are invariant to mean RS and sample size, but remain sensitive to exposure time; finally, (7) M is largely invariant to sample size (except for small samples from highly skewed populations), invariant to mean RS, and largely invariant to exposure time (except in highly skewed populations, where it still outperforms Morisita’s index and I of RS rate). (Online version in colour.)