Figure 12:

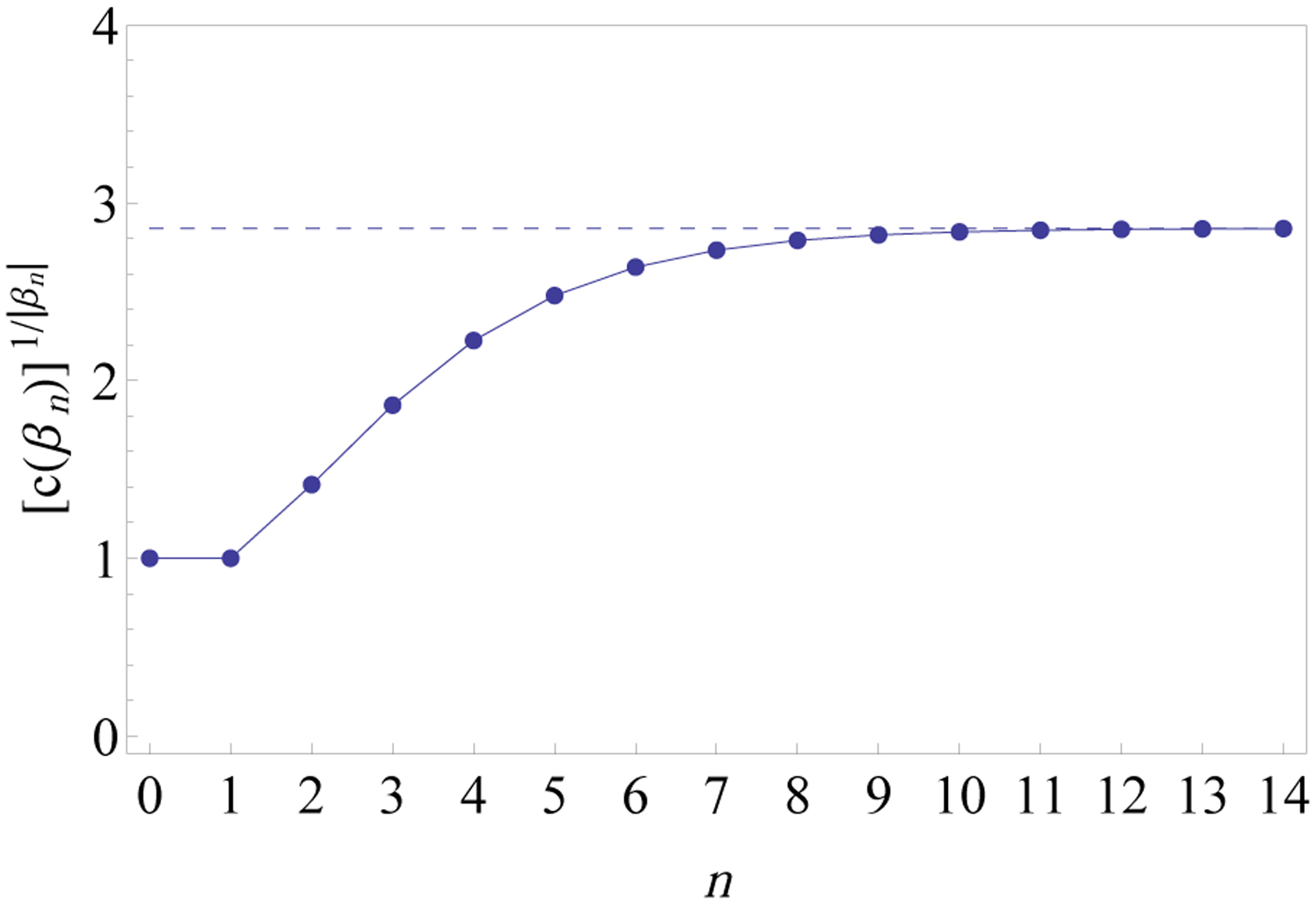
Values of $c({\beta }_n{)}^{1/|{\beta }_n|}$ for 0 ≤ n ≤ 14. The dashed horizontal line has ordinate 2.8565 given by the mean of the lower and upper bounds found for the exponential order k_β for the increase in the number of taxa of compact histories for the completely balanced trees (Eq. 8). The integers c(β_n) are computed as c(β_n) = B_n(1), that is, by setting x = 1 in the polynomials B_n(x) obtained recursively from Proposition 15. The last few points are very closely approximated by the horizontal line. As $c\left({\beta }_n\right)\bowtie k_{\beta }^{|{\beta }_n|}$, for increasing n, the sequence $c({\beta }_n{)}^{1/|{\beta }_n|}$ approaches k_β.