Figure 13:
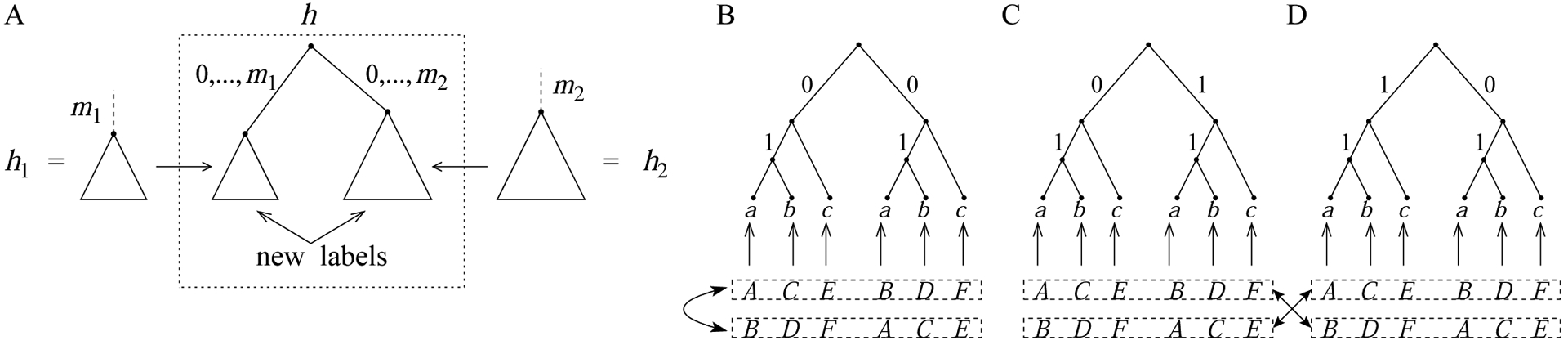
Generation of compact histories from compact histories of smaller trees. (A) Generation of a compact history for a tree from compact histories for its two root subtrees. (B) Generating the same compact history twice when h1 = h2 and ℓ1 = ℓ2. (C,D) Generating the same compact history twice when h1 = h2 and ℓ1 ≠ ℓ2. Each compact history h of size |h| > 1 is obtained as in (A) by (i) appending to a common root node a pair (h1, h2) of compact histories, and (ii) choosing labels ℓ1, ℓ2 for the two branches descending from the root of h. If m1 = m(h1) and m2 = m(h2) are the labels of the root branches of h1 and h2, respectively, then ℓ1 ranges in the interval ℓ1 ∈ [0,m1], and ℓ2 ranges in ℓ2 ∈ [0, m2]. The label of the root branch in h is thus m(h) = m1 + m2 + 1 − ℓ1 − ℓ2, which provides the exponent assigned to variable x in Eq. 28. After step (ii), taxa of h1 and h2 are relabeled to obtain a proper labeled topology underlying h. As in Section 2.1, we impose without loss of generality a linear order ≺ for the labels of the taxa of a tree. For the relabeling procedure, we choose |h1| elements among the |h| = |h1|+ |h2| new labels possible for the taxa of h, where we are using |h|, |h1|, and |h2| here to indicate the number of taxa in the trees underlying h, h1, and h2, respectively. There are different choices, producing the binomial coefficient in Eq. 28. The elements chosen relabel h1, and the remaining elements relabel h2. With respect to the order ≺, the ith label of h1 is assigned the ith label selected. Similarly, the ith label of h2 is assigned the ith label that was not selected. This construction generates each compact history exactly twice. For this reason, the factor 1/2 appears in Eq. 28 before the summations. More precisely, if the pair (h1, h2) considered in step (i) of the procedure has h1 ≠ h2, then each resulting compact history has a copy when we take the pair (h2, h1). If h1 = h2, and we take ℓ1 = ℓ2 in step (ii), then the relabelings generate each compact history twice, as can be seen in (B) by switching the labels assigned to h1 and h2. Finally, if h1 = h2 and we set ℓ1 ≠ ℓ2 in step (ii), then each compact history generated has an equivalent one obtained as in (C) and (D) by switching both the values of ℓ1 and ℓ2 and the labels assigned to h1 and h2.
