Abstract
Accurate estimations of the seroprevalence of antibodies to severe acute respiratory syndrome coronavirus 2 need to properly consider the specificity and sensitivity of the antibody tests. In addition, prior knowledge of the extent of viral infection in a population may also be important for adjusting the estimation of seroprevalence. For this purpose, we have developed a Bayesian approach that can incorporate the variabilities of specificity and sensitivity of the antibody tests, as well as the prior probability distribution of seroprevalence. We have demonstrated the utility of our approach by applying it to a recently published large-scale dataset from the US CDC, with our results providing entire probability distributions of seroprevalence instead of single-point estimates. Our Bayesian code is freely available at https://github.com/qunfengdong/AntibodyTest.
Keywords: COVID-19, SARS-CoV-2, antibody test, Bayesian, specificity, sensitivity
LAY SUMMARY
To estimate the extent of the viral infection, we have developed a statistical method that can incorporate the variabilities of specificity and sensitivity of the antibody tests. Our computer code is freely available at https://github.com/qunfengdong/AntibodyTest.
INTRODUCTION
Antibody tests for COVID-19 have been increasingly deployed to estimate the seroprevalence of antibodies to severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2).1 Although antibody tests can provide important estimations on the prevalence of the viral infection in populations, the test results must be interpreted with caution due to the presence of false positives and false negatives.2 Therefore, a critical statistical challenge is how to accurately estimate the prevalence of the viral infection in populations while accounting for the false positive and false negative rates of the antibody tests.
Recently, the US Centers for Disease Control and Prevention (CDC) published a large-scale study on antibody tests from 10 sites in the US administered between March 23 and May 12, 2020.3 The CDC antibody tests employed an enzyme-linked immunosorbent assay with a specificity (ie, 1 – false positive rate) of 99.3% (95% CI, 98.3%–99.9%) and sensitivity (ie, true positive rate) of 96.0% (95% CI, 90.0%–98.9%).3 In order to take the test accuracy into the consideration, the CDC study applied the following simple correction: Robs = PSensitivity + (1-P) (1-Specificity), where Robs is the observed seroprevalence in the study samples and P is the unknown seroprevalence in populations. Using the point estimates of the sensitivity (96.0%) and specificity (99.3%) of the antibody tests, they obtained the point estimate of the population prevalence P = (Robs – 0.007)/0.953.
There are two main limitations with such an approach. First, only the point estimate of population prevalence P was obtained. Although the CDC study also generated confidence intervals for the point estimate based on a non-parametric bootstrap procedure, the confidence interval does not provide a probabilistic measurement of the uncertainty associated with all possible values of the unknown prevalence. Second, the above CDC approach could not account for any prior knowledge of the population prevalence P, which can lead to inaccurate estimation especially when the true rate of viral infection is low, even with high specificity and sensitivity of the tests.4,5
To overcome the above limitations, we have developed a Bayesian approach. Our approach is not a simple application of Bayes’ theorem by plugging in the point estimates of sensitivity and specificity into the formula and computing a posterior probability. Instead, our approach is a full Bayesian procedure that models the known variability in the sensitivity (95% CI, 90.0%–98.9%) and specificity (95% CI, 98.3%–99.9%) of the antibody test, and we can incorporate any prior knowledge of the viral infection rate to estimate the entire posterior probability distribution of the unknown population prevalence.
MATERIALS AND METHODS
Bayesian modeling
Let Nt and Np denote the number of people tested in total and the number of people tested as positive, respectively. Let p denote the unknown seroprevalence of antibodies to SARS-CoV-2. Let θ denote the true positive rate of the antibody test (ie, sensitivity). Let κ denote the false positive rate of the test (ie, 1 – specificity). Then, we can define the following likelihood function:
| (1) |
In Eq. (1), the term (pθ + (1 − p)κ)Np corresponds to the probability of observing Np people that have tested positive, since a person with a positive test result can either be infected (with the probability of p) and correctly test positive (with the probability of θ), or not infected (with the probability of 1 − p) and falsely test positive (with the probability of κ). Similarly, the term (p(1-θ) + (1 − p)κ)(Nt–Np) corresponds to the probability of observing (Nt–Np) people whose test results were negative.
To estimate the posterior probability of p, we need to sample from the following posterior distribution:
| (2) |
To specify the prior distribution for p, κ, and θ, we chose beta distributions as they are commonly used to model probabilities.6
| (3) |
| (4) |
| (5) |
where αp, βp, ακ, βκ, αθ, and βθ denote shape parameters of the corresponding beta distributions.
For the unknown parameter p, we chose to use a non-informative flat prior probability distribution for this study (ie, αp = βp = 1), although it can be adjusted if prior knowledge of the proportion of infected people for a particular region is known (see more in the Discussion section). For κ and θ, we chose informative priors to reflect the known specificity and sensitivity of a particular antibody test. Specifically, the shape parameters of ακ, βκ, αθ, and βθ can be estimated using the method of moments5 as follows:
| (6) |
| (7) |
| (8) |
| (9) |
where µκ and σκ2, and µθ and σθ2 represent the mean and variance of the test specificity and sensitivity, respectively. For this study, the mean of specificity and sensitivity is 99.3% and 96.0%, respectively. The variances of specificity and sensitivity were approximated7 as s(1-s)/n, where s is the mean value of specificity or sensitivity, and n = 618 according to the CDC validation study on the antibody test accuracy.8
We used WinBUGS9 (version 1.4.3) to implement the above models. In particular, the likelihood function was implemented using the “ones trick”10 of WinBUGS (see the GitHub repository https://github.com/qunfengdong/AntibodyTest for the implementation details). The posterior distributions were estimated with the Markov Chain Monte Carlo (MCMC) sampling in WinBUGS using the following parameters: the number of chains of 4, the number of total iterations of 100 000, burn-in of 10 000, and thinning of 4. Convergence and autocorrelations were evaluated with trace/history/autocorrelation plots and the Gelman–Rubin diagnostic.11 Multiple initial values were applied for MCMC sampling. The above Bayesian procedure was validated with simulated datasets generated by our customized R12 script (available in the above GitHub repository).
Seroprevalence data
The seroprevalence data was taken from the aforementioned CDC publication.3 Our approach requires two inputs: (i) the total number of tested samples and (ii) the number of positive samples. For this project, we only focused on gender-specific data in the CDC study. We extracted the total number of male and female samples from the original Table 1 in the CDC publication. However, the number of positive samples was not reported in the CDC publication. To infer those numbers for both genders, we extracted the CDC estimated seroprevalence, P, for both genders from the original Table 2 in the CDC publication. Using the equation P = (Robs – 0.007)/0.953 mentioned above, we obtained the observed seroprevalence Robs for both genders, which were used for calculating the number of observed positive male and female samples by multiplying Robs to the total number of samples in each respective gender. Table 1 lists the calculated number of test positive samples, rounded to the nearest integer in each site.
Table 1.
Number of positive samples calculated from the CDC publication3
| Sites | Number of positive samples (number of total samples) |
|
|---|---|---|
| Female | Male | |
| Western Washington State | 31 (1930) | 27 (1334) |
| New York City metro area | 73 (1333) | 65 (1149) |
| Louisiana | 45 (677) | 36 (507) |
| South Florida | 20 (964) | 22 (778) |
| Philadelphia metro area | 8 (422) | 14 (402) |
| Missouri | 25 (1018) | 32 (864) |
| Utah | 16 (673) | 13 (465) |
| San Francisco Bay area | 4 (653) | 11 (571) |
| Connecticut | 28 (729) | 43 (702) |
| Minneapolis metro area | 12 (454) | 6 (406) |
Table 2.
Estimated seroprevalence of antibodies to SARS-CoV-2 in populations
| Sites | CDC estimate3 (95% confidence interval), % |
Posterior median (95% credible interval), % |
||
|---|---|---|---|---|
| Female | Male | Female | Male | |
| Western Washington State | 1.7 (0.7–1.9) | 1.4 (0.8–2.4) | 1.0 (0.2–1.9) | 1.5 (0.4–2.5) |
| New York City metro area | 5.7 (4.2–7.0) | 5.9 (4.5–7.6) | 5.0 (3.6–6.5) | 5.3 (3.8–6.9) |
| Louisiana | 7.0 (4.7–9.4) | 6.8 (4.2–9.3) | 6.3 (4.4–8.6) | 6.8 (4.6–9.5) |
| South Florida | 2.2 (1.2–3.4) | 2.2 (1.1–3.6) | 1.5 (0.4–2.8) | 2.3 (1.0–3.8) |
| Philadelphia metro area | 1.9 (0.7–3.7) | 3.0 (1.3–5.2) | 1.5 (0.2–3.2) | 3.1 (1.3–5.4) |
| Missouri | 2.6 (1.5–3.7) | 3.1 (1.8–4.6) | 1.9 (0.7–3.2) | 3.2 (1.8–4.8) |
| Utah | 2.5 (1.2–4.1) | 2.2 (0.9–3.6) | 1.9 (0.6–3.4) | 2.4 (0.8–4.3) |
| San Francisco Bay area | 0.7 (0.2–1.9) | 1.2 (0.4–2.7) | 0.3 (0.02–1.2) | 1.4 (0.3–3.0) |
| Connecticut | 4.1 (2.6–5.9) | 5.7 (3.8–7.6) | 3.4 (1.9–5.1) | 5.8 (3.9–7.9) |
| Minneapolis metro area | 2.7 (1.2–4.8) | 0.7 (0–2.3) | 2.2 (0.7–4.2) | 1.1 (0.1–2.7) |
RESULTS
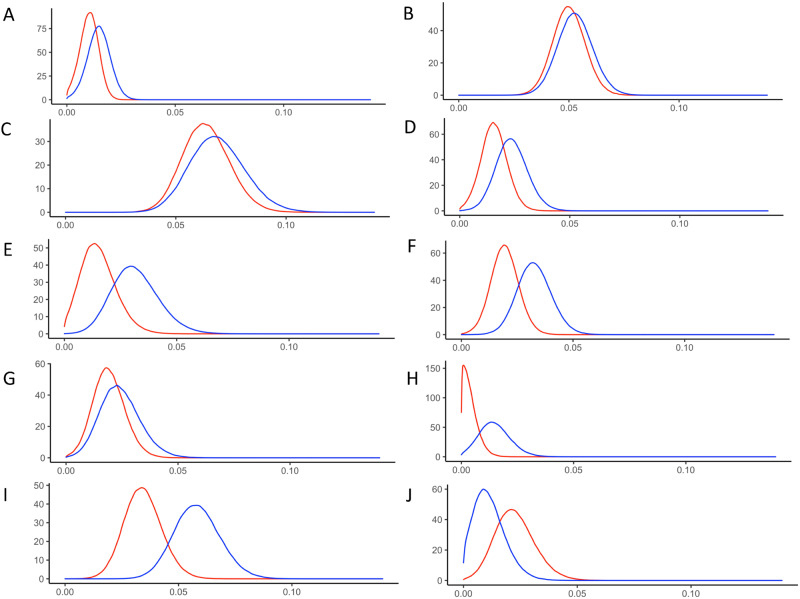
We applied our Bayesian approach to the data listed in Table 1. It is important to emphasize that Bayesian approaches produce entire probability distributions instead point estimates.6Figure 1 depicts the posterior distributions of the seroprevalence of antibodies to SARS-CoV-2 virus in 10 US sites. Table 2 lists both the original CDC point estimates with the accompanying 95% confidence intervals, and our Bayesian estimates, which were presented as the medians and 95% credible intervals of the posterior distributions. It is worth noting that confidence intervals and Bayesian credible intervals are two different concepts,13 thus they are not technically comparable despite being listed together in Table 2 for convenience.
Figure 1.
The posterior probability density of the prevalence of female (red) and male (blue) infected by SARS-CoV-2 virus in 10 US sites: (A) Western Washington State, (B) New York City metro area, (C) Louisiana, (D) South Florida, (E) Philadelphia metro area, (F) Missouri, (G) Utah, (H) San Francisco Bay area, (I) Connecticut, and (J) Minneapolis metro area.
DISCUSSION
Antibody tests have been increasingly applied to estimate the prevalence of people who have been infected by the SARS-CoV-2 virus. For example, New York City recently released data of more than 1.46 million coronavirus antibody test results on August 18, 2020. Accurately analyzing such data is critical for developing important public health policies.14 Our Bayesian approach can explicitly model the variabilities in the sensitivity and specificity of the antibody tests instead of treating them as fixed values. Some subtle differences did exist between our Bayesian estimates and the original CDC estimates; additional simulation studies in the future are required to investigate exact causes of those discrepancies. Nonetheless, the entire posterior distributions (Figure 1) inferred by our Bayesian approach capture the uncertainties associated with seroprevalence. Specifically, the Bayesian approach provided a precise probability associated with every possible value of seroprevalence. Since many of those values may have non-negligible likelihoods, they should not be ignored when public health policy decisions are made on the basis of the seroprevalence. In addition, the Bayesian approach can easily incorporate prior knowledge of the proportion of infected people for a particular region. This is particularly important for accurate estimation if the true prevalence is low.5 Moreover, the Bayesian approach also provides a natural framework for updating the estimation based on new data, which is particularly relevant to the continuous monitoring of the seroprevalence of coronavirus antibodies. For example, New York City is still releasing coronavirus antibody test results on a weekly basis.15 By turning the estimated posterior distribution from previous weeks into a prior distribution for the next week, the seroprevalence of coronavirus antibody can be quickly updated within a solid Bayesian probabilistic inference framework.
AUTHOR CONTRIBUTIONS
QD and XG both contributed project conception. QD contributed WinBUGS modeling and drafting the manuscript. XG contributed R programming and data analysis.
CONFLICT OF INTEREST STATEMENT
None declared.
REFERENCES
- 1. Abbasi J. The promise and peril of antibody testing for COVID-19. JAMA 2020; 323 (19): 1881–3. [DOI] [PubMed] [Google Scholar]
- 2. Kumleben N, Bhopal R, Czypionka T, et al. Test, test, test for covid-19 antibodies: the importance of sensitivity, specificity and predictive powers. Public Health 2020; 185: 88–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Havers FP, Reed C, Lim T, et al. Seroprevalence of antibodies to SARS-CoV-2 in 10 SITES in the United States, March 23-May 12, 2020. JAMA Intern Med 2020; doi: 10.1001/jamainternmed.2020.4130. [DOI] [PubMed] [Google Scholar]
- 4. Weiss SH, Wormser GP.. COVID-19: understanding the science of antibody testing and lessons from the HIV epidemic. Diagn Microbiol Infect Dis 2020; 98 (1): 115078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Mahtur G, Mahtur S.. Antibody testing for COVID-19: can it be used as a screening tool in areas with low prevalence? Am J Clin Pathol 2020; 154: 1–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB.. Bayesian Data Analysis.3rd ed. London: Chapman & Hall; 2013. [Google Scholar]
- 7. Triola MF. Elementary Statistics. 9th ed. New York City, NY: Pearson; 2004. [Google Scholar]
- 8. Freeman B, Lester S, Mills L, et al. Validation of a SARS-CoV-2 spike protein ELISA for use in contact investigations and sero-surveillance. bioRxiv 2020.04.24.057323; doi: 10.1101/2020.04.24.057323. [Google Scholar]
- 9. Lunn DJ, Thomas A, Best N, Spiegelhalter D.. WinBUGS—a Bayesian modelling framework: concepts, structure, and extensibility. Stat Comput 2000; 10 (4): 325–37. [Google Scholar]
- 10. Lunn D, Jackson C, Best N, Thomas A, Spiegelhalter D.. The BUGS Book: A Practical Introduction to Bayesian Analysis. Boca Raton, FL: Chapman and Hall/CRC; 2013. [Google Scholar]
- 11. Gelman A, Rubin DB.. Inference from iterative simulation using multiple sequences (with discussion). Stat Sci 1992; 7 (4): 457–72. [Google Scholar]
- 12.R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2020. https://www.R-project.org/.
- 13. Hespanhol L, Vallio CS, Saragiotto BT, Costa LCM.. Understanding and interpreting confidence and credible intervals around effect estimates. Braz J Phys Ther 2019; 23 (4): 290–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Altmann DM, Douek DC, Boyton RJ.. What policy makers need to know about COVID-19 protective immunity. Lancet 2020; 395 (10236): 1527–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. https://www1.nyc.gov/site/doh/covid/covid-19-data-testing.page Accessed August 20, 2020.