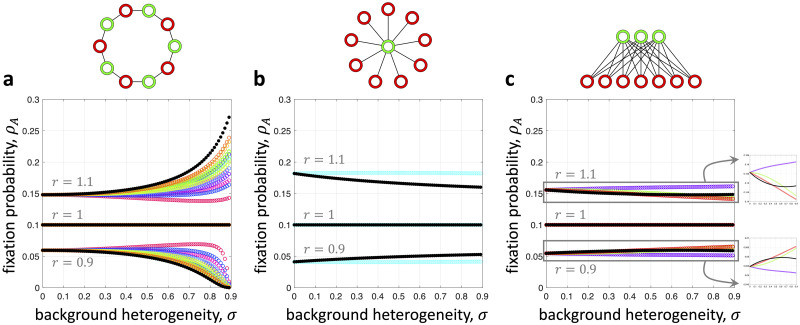
Fig 4. Effects of background heterogeneity for alternative colorings on two-colorable graphs.

In each panel, we plot fixation probability against background heterogeneity for all (non-isomorphic) permutations of the proper two-coloring shown at the top. The proper two-coloring in each case is depicted in black, which is given by Eq 2. a, On the cycle, the proper two-coloring is “optimal” in the sense that it gives the maximum fixation probability for an advantageous mutant and the minimum fixation probability for a disadvantageous mutant. b, On the star, we observe the opposite behavior, with the proper two-coloring giving the minimum fixation probability for an advantageous mutant and the maximum for a disadvantageous mutant. c, On a complete bipartite graph with N_G ≠ N_R (shown here with N_G = 3 and N_R = 7), a mixture of these two results is possible. In particular, there need not be a coloring that is “optimal” for all levels of background heterogeneity. The fixation probabilities in all panels were approximated by building transition matrices for each process and looking at the exact distribution after 10⁷ steps.