Examining the correlation between the weather conditions and COVID-19 pandemic in India: A mathematical evidence

Abstract

In this article, for the analysis of Covid-19 progression in India, we present new insights to formulate a data-driven epidemic model and approximation algorithm using the real data on infection, recovery and death cases with respect to weather in the view of mathematical variables.

Introduction

A novel coronavirus, predominantly called SARS-CoV-2 a severe respiratory syndrome coronavirus, was first recorded in one of the industrial city of China, so-called, Wuhan in December 2019. The outbreak of novel coronavirus (2019-nCoV) was declared a Public Health Emergency of International Concern (PHEIC) by the WHO at a meeting on January 30 2020, according to the International Health Regulations (IHR, 2005) emergency commission, as it had spread to countries and with four countries confirming human-to–human transmission. COVID-19’s initial case was filed on January 30, 2020, in India, with origin from China (PIB, 2020). It extends down to the country’s highest districts. On 24th March, India’s government-mandated a 21-day nationwide curfew, restricting the movement of India’s entire population of 1.3 billion as a precautionary action against India’s 2020 coronavirus disease outbreak. It was decided to order on March 22nd, after a 14 h volunteer public shutdown, accompanied by the implementation of a set of restrictions in the COVID-19 infected areas of the country. The lockdown was imposed when reportedly 500 reported positive COVID-19 cases were identified in India. The lockdown regulates restrictions and initiatives of self-quarantine. Lockdown was retained all across until May 3rd, with a nominal exemption provided for the parts of the country where the spread has been controlled by that time after April 20th. The impact of environmental conditions on virus transmission has always been an important discussion topic among the investigators. Studies pertinent to West Nile Virus studies in the United States and Europe declare the connection between climate conditions and SARS-CoV and imply that weather variable might even be the source of metabolic pathways between SARS-CoV and humans. The environment is very strongly correlated with pneumonia-related improvements in mortality rates and death rates. The spread of the virus infections is affected by multiple factors, such as clouding, temperature, humidity and density of population. Correlation between the weather conditions and COVID-19 in Jakarta, Indonesia and claimed essential findings in this direction. In the Indian perspective, COVID-19 investigation is very restricted, in particular, the impact of climate change on the COVID-19 pandemic. Undoubtedly the present study will serve as new insight in this direction and will be useful for further analysis to arrive at a precise conclusion.

In statistical methods, among the most critical problems when concerned with data is the correlation coefficient. The coefficient of correlation r (Pearson’s Coefficient), proposed by Karl Pearson in 1885, is now one of the most commonly used indices. It has been proven to be a powerful tool in data processing, psychological disorders, market research, pattern classification, and in particular for problems in strategic decisions. Gerstenkorn and Manko [13], formulated the correlation coefficients of intuitionistic fuzzy sets (shortly, IFSs), which were subsequently studied by Szmidt and Kacprzyk [34], Bustince and Burillo [8], further expanded the principles of correlation and correlation coefficient for interval-valued intuitionistic fuzzy sets (shortly, IVIFSs). Hung and Wu [15] suggested a strategy for using centroid to find the correlation coefficients of IFSs.

Another natural outcome is intuitionistic fuzzy sets (shortly, A-IFSs) by Atanassov. A relationship between A-IFSs and IFSs also seems to be vital importance, so in this direction, several reports have addressed the A-IFS correlation. In most other papers (Gersternkorn and Mańko [13], Hong and Hwang [14], Hung and Wu [15]), a pro and con type of relationship is represented. However, no account has been taken of its third term describing an A-IFS, the hesitation margin in addition to the membership and non-membership degrees shown to be significant from the perspective of similarity, distance or entropy measures (cf. Szmidt and Kacprzyk, e.g., [31], [32], [33], [34], [35]).

Molodtsov [25] introduced the concept fuzzy soft set theory in 1999, and it was greatly extended in wide directions by Maji et. al., [20], [21], [22]. Numerous researchers subsequently worked on several aspects of fuzzy soft sets, which are intuitive fuzzy soft sets [23], interval-valued fuzzy soft sets [40], intuition-valued fuzzy soft sets [16] etc. Correlation coefficient analysis is one of the important components of fuzzy soft sets. Das et al. [12] investigated the problem of measuring the correlation between the hesitant fuzzy soft sets. For similarity measurements of soft sets and related implementations, readers can also see [5], [6], [7].

2019-nCoV terrifies the world. The virus first seen in Wuhan, China, has spread through continents. The increase in deaths in Italy, Spain, the US, and other countries has worried advanced and emerging economies countries alike. The smallest creature, invisible to the eye, questions the existence of humankind. Covid-19 combat is still in its early stages. Researchers [1], [4], [24], [27], [28], [29] are currently working on multiple investigative paths. The first case of the novel coronavirus disease 2019 (COVID-19) was identified at the end of 2019 in the city of Wuhan China, which is the provincial capital of Hubei. After acquiring pneumonia without a specific cause and the available vaccine or therapies be not successful for that. Furthermore, the virus is shown to be transmitted from person - to - person. The spread not only across the city of Wuhan but also across the other cities of China. Besides, the disease mutates to other areas of the globe, including Europe, North America and Asia-pacific regions. It is known that it takes 2 to 14 days for symptoms to emerge. The symptoms entail coughing, difficulty breathing and fever. The World Health Organization (WHO) officially announced the spread of the novel coronavirus as a Global Pandemic on March 11, 2020. A total of 9,714,951 cases are reported in over 212 parts of the world as of June 26 2020. There are 3,972,865 reported cases, and the deaths are 491,868. India currently has become Asia’s largest vulnerable country. In India, a total of 491,136 cases are confirmed as of June 26, 2020. There are 190,006 diagnosed cases and a death rate of 15,309. The fatality rate for India is relatively low, at 3.09.

On March 22, 2020, India implemented a 14-h volunteer public curfew accompanied by a nationwide lockdown since March 24, 2020, in response to many other steps such as quarantine of suspicious cases, social distance guidelines for public health, regular personal hygiene and wearing face masks when leaving home for critical services. India’s government is considering several lockdowns to avoid the virus from spreading. Initially, in lockdown 1.0 (March 25, 2020, to April 14, 2020), the whole nation was under total lockdown except for essential public services, and lockdown 2.0 (April 15, 2020, to May 3, 2020) was enacted with relaxation in regions where the virus has consisted and lockdown 3.0 (May 4, 2020, to May 17, 2020) with more relaxation in areas where there would be fewer cases of corona-virus. Lockdown 4.0 (May 18, 2020, to May 31, 2020) with certain significant exemptions, allowing for all commercial development and sizeable international movement. With further relaxation after this Unlock 1.0 (June 1, 2020, to June 30, 2020) and Unlock 2.0 (July 1, 2020, to July 31, 2020) are introduced. Intend to note that, on these lockdowns, the number of cases has been decreased.

Human-to-human replication, meteorological parameters are believed to be important influences in the feasibility, propagation, and range of virus spread (Chan et al. [9], Van Doremalen et al. [38]). Zhu and Xie [42] studied the correlation among temperature and COVID-19 contamination in China and reported a positive linear relationship between average temperatures and the number of COVID-19 cases when the temperature is below 3 °C. Also, Tosepu et al. [37] explored the relation in between the weather and the COVID-19 pandemic in Indonesia and concluded that the mean temperature of (°C), is associated with the COVID-19 pandemic. Ma et al. [18] evaluated the influence of temperature and humidity variation on COVID-19 deaths, and asserted that these parameters affect COVID-19 mortality. Chen et al. [10] explored the correlation between meteorological parameters and COVID-19 severity spread worldwide and concluded that air density, temperature, and relative humidity are effective variables. Wang et al. [39] analysed the impact of temperature on COVID-19 spread and reported that COVID-19 transmission is strongly impacted by temperature. The most general objective of this research is to examine the correlation between both the meteorological parameters and pandemic COVID-19. In order to increase the possibility of success against this life-threatening pandemic, the dynamic aspects of SARS-CoV-2 invasion involve cooperation of scientists from multiple disciplines including medical, scientific, and engineering areas [2], [17], [26], [30], [36], [45], [46], [47], [48], [49], [50], [51].

We structure our article as follows: Some preliminary findings are given in Section “Preliminary results”. The definition of correlation between the AIFSSs was discussed in Section “Correlation between A-IFSSs”. We also suggested the idea of the correlation between the intuitionistic fuzzy soft-points of the Atanassov. In Section “Computational methods in A-IFSSs in the context of Covid-19” and “Discussion on correlation between weather conditions and COVID-19 pandemic”, we present an application followed by a discussion on A-IFSSs pertinent to Covid-19.

Preliminary results

In this section we recall some basic concepts and definitions regarding fuzzy sets and fuzzy soft sets.

Definition 1.1 [41] —

Let X be a universe of discourse, then a fuzzy set is defined as, $A=\left\{\right(x,{\mu }_A\left(x\right)):x\in X\}$, which characterize the membership function ${\mu }_A:X⟶[0,1]$, where ${\mu }_A\left(x\right)$ denotes the degree of membership of the element x to the set A.

Atanassov continued to expand the Fuzzy set to the IFS, as shown:

Definition 1.2 [3] —

An intuitionistic fuzzy set A in X is given by, $A=\left\{\right(x,{\mu }_A\left(x\right),{\nu }_A\left(x\right)):x\in X\}$, where ${\mu }_A:X⟶[0,1]$, and ${\nu }_A:X⟶[0,1]$, with the condition $0⩽{\mu }_A\left(x\right)+{\nu }_A\left(x\right)⩽1,\forall x\in X$. The number ${\mu }_A\left(x\right)$ and ${\nu }_A\left(x\right)$ represent, respectively, the membership degree and non-membership degree of the element x to the set A.

Definition 1.3 [3] —

For each intuitionistic fuzzy set A in X, if ${\pi }_A\left(x\right)=1-{\mu }_A\left(x\right)-{\nu }_A\left(x\right),\forall x\in X$. Then ${\pi }_A\left(x\right)$ is called the degree of indeterminacy of x to A.

Proposition 1.4 [3] —

If A and B are two intuitionistic fuzzy sets of the set X, Then

• 1. (i) $A\subset B\mathrm{iff}\forall x\in X,{\mu }_A\left(x\right)⩽{\mu }_B\left(x\right)\mathrm{and}{\nu }_A\left(x\right)⩾{\nu }_B\left(x\right)$ .
• 2. (ii) $A\subset B\mathrm{iff}B\supset A\text{;}A=B\mathrm{iff}\forall x\in X,{\mu }_A\left(x\right)={\mu }_B\left(x\right)\mathrm{and}{\nu }_A\left(x\right)={\nu }_B\left(x\right)$ .
• 3. (iii) $A\cup B=\left\{\right(x,\max \left({\mu }_A\right(x),{\mu }_B(x\left)\right),\min \left({\nu }_A\right(x),{\nu }_B(x\left)\right)):x\in X\}$ .
• 4. (iv) $A\cap B=\left\{\right(x,\min \left({\mu }_A\right(x),{\mu }_B(x\left)\right),\max \left({\nu }_A\right(x),{\nu }_B(x\left)\right)):x\in X\}$ .

Definition 1.5 [11] —

Suppose now that we have a random sample $x_1,x_2,x_3,\dots ,x_n\in X$ with a sequence of paired data

$$\left({\mu }_A\right(x_1),{\mu }_B(x_1\left)\right),\left({\mu }_A\right(x_2),{\mu }_B(x_2\left)\right),\dots ,\left({\mu }_A\right(x_n),{\mu }_B(x_n\left)\right)$$

that correspond to the membership values of fuzzy sets A and B defined on X, then the correlation coefficient $r_f(A,B)$is given as:

$$r_f(A,B)=\frac{{\displaystyle \sum _{i=1}^n}\left({\mu }_A\right(x_i)-\overline{{\mu }_A})\left({\mu }_B\right(x_i)-\overline{{\mu }_B})}{{\left({\displaystyle \sum _{i=1}^n}{\left({\mu }_A\right(x_i)-\overline{{\mu }_A})}^2\right)}^{0.5}{\left({\displaystyle \sum _{i=1}^n}{\left({\mu }_B\right(x_i)-\overline{{\mu }_B})}^2\right)}^{0.5}},$$

where $\overline{{\mu }_A}=\frac{1}{n}{\sum }_{i=1}^n{\mu }_A\left(x_i\right),\overline{{\mu }_B}=\frac{1}{n}{\sum }_{i=1}^n{\mu }_B\left(x_i\right)$.

Definition 1.6 [22] —

Let U be an initial universe and F be a set of parameters. Let $\tilde{P}\left(U\right)$ denote the power set of U and A be a non-empty subset of F. Then $F_A$ is called a fuzzy soft set over U, where $F:A\to \tilde{P}\left(U\right)$ is a mapping from A into $\tilde{P}\left(U\right)$.

Definition 1.7 [19] —

Consider U and E as universe set and a set of parameters respectively. Let $\tilde{P}\left(U\right)$ denotes the set of all intuitionistic fuzzy sets of U. Let $A\tilde{\subset }B$. Then $F_A$ is an intuitioistic fuzzy soft set over U, where F is a mapping given by $F:A\to \tilde{P}\left(U\right)$.

Definition 1.8 [19] —

Two intuitionistic fuzzy soft sets $F_A$ and $G_B$ over a common universe U are said to be fuzzy soft equal if $F_A$ is an intuitionistic fuzzy soft subset of $G_B$ and $G_B$ is an intuitionistic fuzzy soft subset of $F_A$.

Definition 1.9 [22] —

For two fuzzy soft sets $F_A$ and $G_B$ over a common universe U, we say that $F_A$ is a fuzzy soft subset of $G_B$ if (i) $A\tilde{\subset }B$, (ii) $\forall \epsilon \tilde{\in }A,F\left(\epsilon \right)$ is a fuzzy subset of $G\left(\epsilon \right)$.

Definition 1.10 [22] —

Two soft sets $F_A$ and $G_B$ over a common universe U are said to be fuzzy soft equal if $F_A$ is a fuzzy soft subset of $G_B$ and $G_B$ is a fuzzy soft subset of $F_A$.

Correlation between A-IFSSs

In our studies, we consider all Attanssov’s intuionistic fuzzy sets in $\tilde{P}\left(U\right)$,of [19] i.e our new definition is.

Definition 1.11

Consider U and E as universe set and a set of parameters respectively. Let $\tilde{P}\left(U\right)$ denotes the set of all Attanssov’s intuitionistic fuzzy sets of U. Let $A\tilde{\subset }B$. Then $F_A$ is an Attanssov’s intuitioistic fuzzy soft set (A-IFSS) over U, where F is a mapping given by $F:A\to \tilde{P}\left(U\right)$.

Here we consider membership, non-membership values and the hesitant margins of the objects of A-IFSSs. For Example:

$$F_A=\{e_1=\{(h_1,0.2,0.7,0.1),(h_2,0.4,0.5,0.1)\},e_2=\{(h_1,0.1,0.6,0.3),(h_2,0.3,0.5,0.2)\left\}\right\}\text{.}$$

Definition 1.12

Let $F_A$ and $G_B$ be two A-IFSSs over in $(U,E)$. Then the correlation between them, denoted by $\widetilde{r_{A-\mathit{IFSSs}}}(F_A,G_B)$ is defined as

$$r_{\tilde{A}-\mathit{IFSSs}}(F_A,G_B)=\frac{1}{3}\left({\tilde{r}}_1\right(F_A,G_B)+{\tilde{r}}_2(F_A,G_B)+{\tilde{r}}_3(F_A,G_B\left)\right),$$

where

$$\begin{array}{c}\hfill \widetilde{r_1}(F_A,G_B)=\frac{{\displaystyle \sum _{t=1}^n}\left\{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)\left({\mu }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{p+n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_j\left(G_B\right)}\left(h_t\right)\right\}\right)\right\}}{{\left\{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\right(h_t\left)\right\}\right)}^2\right\}}^{0.5}{\left\{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{p+n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_j\left(G_B\right)}\right(h_t\left)\right\}\right)}^2\right\}}^{0.5}},\\ \hfill \widetilde{r_2}(F_A,G_B)=\frac{{\displaystyle \sum _{t=1}^n}\left\{\left({\nu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\nu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)\left({\nu }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{p+n}{\displaystyle \sum _{t=1}^n}\left\{{\nu }_{e_j\left(G_B\right)}\left(h_t\right)\right\}\right)\right\}}{{\left\{{\displaystyle \sum _{t=1}^n}{\left({\nu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\nu }_{e_i\left(F_A\right)}\right(h_t\left)\right\}\right)}^2\right\}}^{0.5}{\left\{{\displaystyle \sum _{t=1}^n}{\left({\nu }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{p+n}{\displaystyle \sum _{t=1}^n}\left\{{\nu }_{e_j\left(G_B\right)}\right(h_t\left)\right\}\right)}^2\right\}}^{0.5}}\\ \hfill \widetilde{r_3}(F_A,G_B)=\frac{{\displaystyle \sum _{t=1}^n}\left\{\left({\pi }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\pi }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)\left({\pi }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{p+n}{\displaystyle \sum _{t=1}^n}\left\{{\pi }_{e_j\left(G_B\right)}\left(h_t\right)\right\}\right)\right\}}{{\left\{{\displaystyle \sum _{t=1}^n}{\left({\pi }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\pi }_{e_i\left(F_A\right)}\right(h_t\left)\right\}\right)}^2\right\}}^{0.5}{\left\{{\displaystyle \sum _{t=1}^n}{\left({\pi }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{p+n}{\displaystyle \sum _{t=1}^n}\left\{{\pi }_{e_j\left(G_B\right)}\right(h_t\left)\right\}\right)}^2\right\}}^{0.5}},\end{array}$$

and $i=1,2,3,\dots ,m\text{;}j=1,2,3,\dots ,p$.

Example 1.13

Let $F_A=\{e_1=\{(h_1,0.2,0.7,0.1),(h_2,0.4,0.5,0.1),(h_3,0.6,0.2,0.2)\},e_2=\{(h_1,0.1,0.6,0.3),(h_2,0.3,0.5,0.2),(h_3,0.5,0.4,0.1)\},G_B=\{e_1=\left\{\right(h_1,0.6,0.3,0.1),(h_2,0.4,0.1,0.5),(h_3,0.3,0.4,0.3\left)\right\},e_2=\left\{\right(h_1,0.9,0.1,0.0),(h_2,0.5,0.2,0.3),(h_3,0.3,0.6,0.1\left)\right\}\}$. Therefore, $\widetilde{r_1}(F_A,G_B)=-0.939\text{;}\widetilde{r_2}(F_A,G_B)=-0.491\text{;}\widetilde{r_3}(F_A,G_B)=-0.360$. Hence $\widetilde{r_{A-\mathit{IFSSs}}}(F_A,G_B)=-0.60$.

Proposition 1.14

Let $F_A$ and $G_B$ be two A-IFSSs over in $(U,E)$ . Then

• 1. (i) $\widetilde{r_{A-\mathit{IFSSs}}}(F_A,G_B)=\widetilde{r_{A-\mathit{IFSSs}}}(G_B,F_A)$ .
• 2. (ii) $\mathrm{If}{F}_A=G_B\mathrm{then}\widetilde{r_{A-\mathit{IFSSs}}}(F_A,G_B)=1$ .
• 3. (iii) $\left|\widetilde{r_{A-\mathit{IFSSs}}}(F_A,G_B)\right|⩽1$ .

Proof

• 1.(i) Obvious.
• 2.
  (ii) For $t=1,2,3,\dots ,n\text{;}i=1,2,3,\dots ,m$ and $j=1,2,3,\dots ,p$. Let $G_B=F_A$, then $i=j$ and $p=m$. Therefore

  $$\begin{array}{c}\hfill \widetilde{r_1}(F_A,F_A)=\frac{{\displaystyle \sum _{t=1}^n}\left\{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)\left({\mu }_{\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)\right\}}{{\left\{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)}^2\right\}}^{0.5}{\left\{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)}^2\right\}}^{0.5}}\\ \hfill =\frac{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)}^2}{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{m+n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)}^2}\\ \hfill =1\text{.}\end{array}$$

  Similarly, $\widetilde{r_2}(F_A,G_B)=1$, and $\widetilde{r_3}(F_A,G_B)=1$.

• 3.(iii) Obvious. .

Definition 1.15

Let $\widetilde{e_i}\left(F_A\right)$ and $\widetilde{e_j}\left(G_B\right)$ be two Atanassov’s intuitionistic fuzzy soft points (A-IFSPs) over in $(U,E)$. Then the correlation between them, denoted by ${\widetilde{r^{\prime }}}_{A-\mathit{IFSSs}}\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)$ is defined as

$${\widetilde{r^{\prime }}}_{A-\mathit{IFSSs}}\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)=\frac{1}{3}\left({\widetilde{r^{\prime }}}_1\right(\widetilde{e_i}\left(F_A\right),\widetilde{e_j}\left(G_B\right))+{\widetilde{r^{\prime }}}_2(\widetilde{e_i}\left(F_A\right),\widetilde{e_j}\left(G_B\right))+{\widetilde{r^{\prime }}}_3(\widetilde{e_i}\left(F_A\right),\widetilde{e_j}\left(G_B\right)),$$

where

$$\begin{array}{c}\hfill {\widetilde{r^{\prime }}}_1\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)=\frac{{\displaystyle \sum _{t=1}^n}\left\{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)\left({\mu }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_j\left(G_B\right)}\left(h_t\right)\right\}\right)\right\}}{{\left\{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)}^2\right\}}^{0.5}{\left\{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_j\left(G_B\right)}\left(h_t\right)\right\}\right)}^2\right\}}^{0.5}},\\ \hfill {\widetilde{r^{\prime }}}_2\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)=\frac{{\displaystyle \sum _{t=1}^n}\left\{\left({\nu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\nu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)\left({\nu }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\nu }_{e_j\left(G_B\right)}\left(h_t\right)\right\}\right)\right\}}{{\left\{{\displaystyle \sum _{t=1}^n}{\left({\nu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\nu }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)}^2\right\}}^{0.5}{\left\{{\displaystyle \sum _{t=1}^n}{\left({\nu }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\nu }_{e_j\left(G_B\right)}\left(h_t\right)\right\}\right)}^2\right\}}^{0.5}}\\ \hfill {\widetilde{r^{\prime }}}_3\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)=\frac{{\displaystyle \sum _{t=1}^n}\left\{\left({\pi }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\pi }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)\left({\pi }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\pi }_{e_j\left(G_B\right)}\left(h_t\right)\right\}\right)\right\}}{{\left\{{\displaystyle \sum _{t=1}^n}{\left({\pi }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\pi }_{e_i\left(F_A\right)}\left(h_t\right)\right\}\right)}^2\right\}}^{0.5}{\left\{{\displaystyle \sum _{t=1}^n}{\left({\pi }_{e_j\left(G_B\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\pi }_{e_j\left(G_B\right)}\left(h_t\right)\right\}\right)}^2\right\}}^{0.5}},\end{array}$$

where $i=1,2,3,\dots m\text{;}j=1,2,3,\dots p$.

Example 1.16

From above Problem 0.13 we have

$$\begin{array}{cc}\hfill & \widetilde{e_1}\left(F_A\right)=\left\{\right(h_1,0.2,0.7,0.1),(h_2,0.4,0.5,0.1),(h_3,0.6,0.2,0.2\left)\right\},\hfill \\ \hfill & \widetilde{e_3}\left(G_B\right)=\left\{\right(h_1,0.9,0.1,0.0),(h_2,0.5,0.2,0.3),(h_3,0.3,0.6,0.1\left)\right\}\text{.}\hfill \end{array}$$

Therefore, ${\tilde{r}}_1^{\prime }\left(\widetilde{e_1}\right(F_A),\widetilde{e_3}(G_B\left)\right)=-1.00\text{;}{\widetilde{r^{\prime }}}_2\left(\widetilde{e_1}\right(F_A),\widetilde{e_3}(G_B\left)\right)=-1.00\text{;}{\widetilde{r^{\prime }}}_3\left(\widetilde{e_1}\right(F_A),\widetilde{e_3}(G_B\left)\right)=-0.180$. Hence ${\widetilde{r^{\prime }}}_{A-\mathit{IFSSs}}\left(\widetilde{e_1}\right(F_A),\widetilde{e_3}(G_B\left)\right)=-0.727$.

Proposition 1.17

Let $\widetilde{e_i}\left(F_A\right)$ and $\widetilde{e_j}\left(G_B\right)$ be two A-IFSSs over in $(U,E)$. Then

• 1.(i) ${\widetilde{r^{\prime }}}_{A-\mathit{IFSSs}}\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)={\widetilde{r^{\prime }}}_{A-\mathit{IFSSs}}\left(\widetilde{e_j}\right(G_B),\widetilde{e_i}(F_A\left)\right)$
• 2.(ii) $\mathrm{If}\widetilde{e_i}\left(F_A\right)=\widetilde{e_j}\left(G_B\right)$ then ${\widetilde{r^{\prime }}}_{A-\mathit{IFSSs}}\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)=1$.
• 3.(iii) $\left|{\widetilde{r^{\prime }}}_{A-\mathit{IFSSs}}\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)\right|⩽1$.

Proof

• 1.(i) Obvious.
• 2.
  (ii) For $t=1,2,3,\dots ,n\text{;}i=1,2,3,\dots ,m$ and $j=1,2,3,\dots ,p$. Let $\widetilde{e_j}\left(G_B\right)=\widetilde{e_i}\left(F_A\right)$, then $i=j$and $p=m$. Therefore

  $$\begin{array}{c}\hfill {\widetilde{r^{\prime }}}_1\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)=\frac{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\right(h_t\left)\right\}\right)}^2}{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\right(h_t\left)\right\}\right)}^2}\\ \hfill =\frac{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\right(h_t\left)\right\}\right)}^2}{{\displaystyle \sum _{t=1}^n}{\left({\mu }_{e_i\left(F_A\right)}\left(h_t\right)-\frac{1}{n}{\displaystyle \sum _{t=1}^n}\left\{{\mu }_{e_i\left(F_A\right)}\right(h_t\left)\right\}\right)}^2}\\ \hfill =1\text{.}\end{array}$$

  Similarly, ${\widetilde{r^{\prime }}}_2\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)=1$, and ${\widetilde{r^{\prime }}}_3\left(\widetilde{e_i}\right(F_A),\widetilde{e_j}(G_B\left)\right)=1$.
• 3.(iii) Obvious.

Definition 1.18

If two Atanassov’s intuitionistic fuzzy soft points correlation in same set then this correlation is called inter correlation of A-IFSS.

Example 1.19

From above Problem 1.13, we have, $\widetilde{e_1}\left(F_A\right)=\left\{\right(h_1,0.2,0.7,0.1),(h_2,0.4,0.5,0.1),(h_3,0.6,0.2,0.2\left)\right\},\widetilde{e_2}\left(F_A\right)=\left\{\right(h_1,0.1,0.6,0.3),(h_2,0.3,0.5,0.2),(h_3,0.5,0.4,0.1\left)\right\}$. Therefore,${\widetilde{r^{\prime }}}_1\left(\widetilde{e_1}\right(F_A),\widetilde{e_2}(F_A\left)\right)=1.00\text{;}{\widetilde{r^{\prime }}}_2\left(\widetilde{e_1}\right(F_A),\widetilde{e_2}(F_A\left)\right)=1.00\text{;}{\widetilde{r^{\prime }}}_3\left(\widetilde{e_1}\right(F_A),\widetilde{e_2}(F_A\left)\right)=-1.00$. Hence ${\widetilde{r^{\prime }}}_{A-\mathit{IFSSs}}\left(\widetilde{e_1}\right(F_A),\widetilde{e_2}(F_A\left)\right)=0.34$.

Computational methods in A-IFSSs in the context of Covid-19

Now India has become largest affected country of Covid-19 in Asia. It is easy to see that the virus scattered across the country as the worst affected states being Maharashtra (375,495 cases), Tamil Nadu (213,723), Delhi (130,606), Andhra Pradesh (96,298) and Karnataka (96,132) on July 26, 2020.

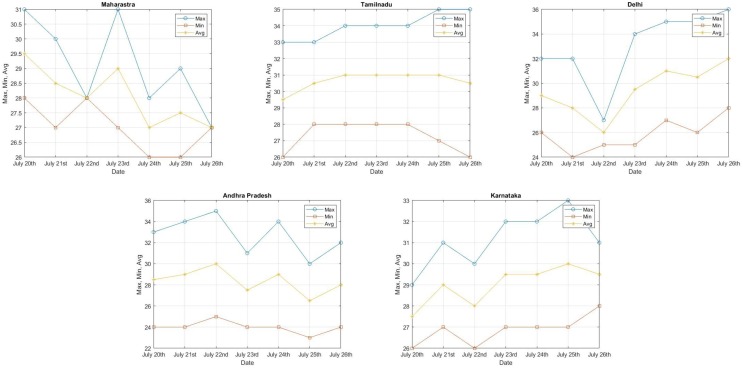
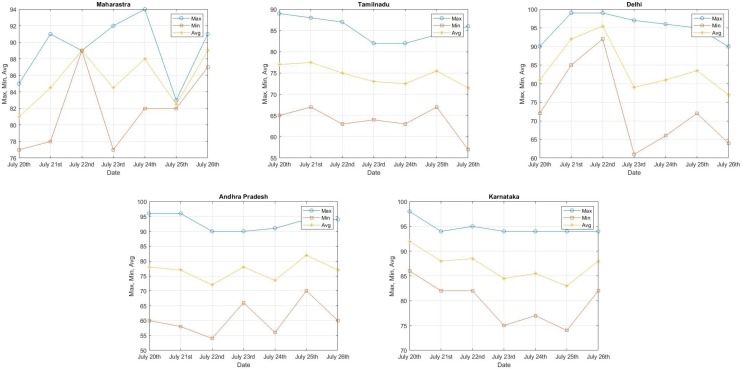
In this section, we have tried to established correlation between Confirmed cases (Active + Recovered + Deceased) in Covid19 and temperature of particular States; Confirmed cases (Active + Recovered + Deceased) in Covid19 and humidity of particular States. Here we have collected data five states in India which are Maharastra, Tamil Nadu, Delhi, Andhra Pradesh and Karnataka. The computerized data set on daily covid-19 in India for the period of July 20 - July 26, 2020 were obtained from crowdsourced database of COVID-19 India dot org [43], while the weather data for the period of July 20-July 26, 2020 were obtained from the meteorological website timeanddate dot com [44]. The data consist of temperature minimum (°C), temperature maximum (°C), temperature average (°C), humidity maximum (%), humidity minimum (%) and humidity average (%). see Fig. 1, Fig. 2 .

Fig. 1.

Variation in minimum, maximum and average temperatures (°C) of the States.

Fig. 2.

Variation in minimum, maximum and average humidities (°C) of the States.

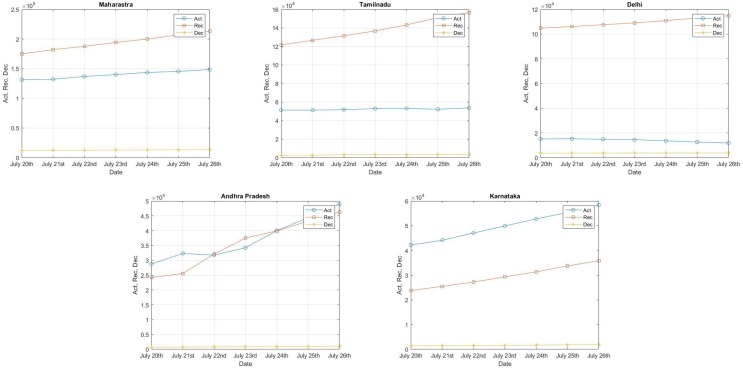
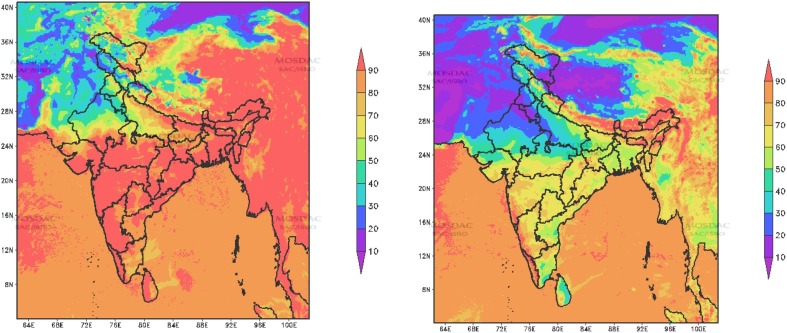
We used the following algorithms. see Fig. 3, Fig. 4 .

Fig. 3.

Confirmed Cases(Active + Recovered + Deceased).

Fig. 4.

Reference map of the study area showing air temperature for the month of July, 2 m height Temperature(C) and relative humidity($\%$).

Algorithms:

• 1.Step(i) To collect maximum, minimum and average temperature data of five states from timeanddate dot com in tabular form.
• 2.Step(ii) To convert Step (i) data to decimal form.
• 3.Step(iii) To collect maximum, minimum and average humidity data of five states from timeanddate.com in tabular form.
• 4.Step(iv) To convert Step (iii) data to decimal form.
• 5.Step(v) To Collect data of five states from crowdsourced database of COVID-19 India dot org.
• 6.Step(vi) To convert Step (v) data to decimal form.
• 7.Step(vii) Find the correlation between A-IFSSs of Step (ii) and Step (vi).
• 8.Step(viii) Arranged Step(ii) data as average, maximum and minimum then find the correlation between A-IFSSs of arranged data and Step (vi).
• 9.Step(ix) Arranged Step(ii) data as minimum,average and maximum then find the correlation between A-IFSSs of arranged data and Step (vi).
• 10.Step(x) Find the correlation between A-IFSSs of Step (iv) and Step (vi).
• 11.Step(xi) Arranged Step(iv) data as average, maximum and minimum then find the correlation between A-IFSSs of arranged data and Step (vi).
• 12.Step(xii) Arranged Step(iv) data as minimum,average and maximum then find the correlation between A-IFSSs of arranged data and Step (vi).
• 13.Step(xiii) finally expressed Step (vii), Step (viii), Step (ix), Step (x), Step (xi) and Step (xii) in tabular form.

Discussion on correlation between weather conditions and COVID-19 pandemic

As noted earlier, the analysis considers two key variables, namely temperature and humidity. These two variables (temperature and humidity) are analysed for a one-week data with Active cases, Recovered cases and Decreased cases. First, the correlation between temperature (as Maximum, Minimum and Average) and the number of total cases (as Active, Recovered and Decrease) in each state is evaluated. Secondly, correlation between temperature (as Average, Maximum and Minimum) and the number of total cases (as Active, Recovered and Decreased) in each state is evaluated. Finally, correlation between temperature (as Minimum, Average and Maximum) and the number of total cases (as Active, Recovered and Decreased) in each state is evaluated. Similar way, we have found the correlation between humidity and the total number of cases. The data from the Table 3, Table 5 has been summarized in the Fig. 4. To explicate the affect of weather conditions on transmission occurring in India, temperature(C) and relative humidity($\%$) over 5 most affected states are analysed for the month of July as shown in Fig. 4 as per in Table 1, Table 2, Table 4 and Table 6, Table 7 . Moreover, Table 8 presents the result of correlation analysis. The results indicate that the temperature and humidity are maximum, the active cases and deceased are inverse correlation. The correlation is inverse, which implies that as the temperature and humidity are lower, the number of cases increase. Again the temperature is maximum than the Recovered cases are positive correlation and humidity is average than the recovered cases are positive correlation.

Table 3.

Temperature in converted form.

Date	Maharashtra			Tamil Nadu			Delhi			Andhra Pradesh			Karnataka
	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg
July 20	.350	.316	.334	.373	.294	.333	.368	.299	.333	.386	.281	.333	.352	.315	.333
July 21	.351	.316	.333	.361	.306	.333	.381	.286	.333	.391	.276	.333	.356	.310	.334
July 22	.334	.333	.333	.366	.301	.333	.346	.321	.333	.389	.278	.333	.357	.310	.333
July 23	.356	.310	.334	.366	.301	.333	.384	.282	.334	.376	.291	.333	.362	.305	.333
July 24	.346	.321	.333	.365	.301	.333	.376	.290	.334	.391	.276	.333	.362	.305	.333
July 25	.352	.315	.333	.376	.290	.334	.383	.284	.333	.377	.289	.334	.367	.300	.333
July 26	.334	.333	.333	.382	.284	.334	.375	.292	.333	.381	.286	.333	.350	.316	.334

Table 5.

Humidity in converted form.

Date	Maharashtra			Tamil Nadu			Delhi			Andhra Pradesh			Karnataka
	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg
July 20	.350	.317	.333	.385	.281	.334	.370	.296	.334	.410	.256	.334	.355	.312	.333
July 21	.359	.308	.333	.378	.288	.334	.359	.308	.333	.416	.251	.333	.356	.311	.333
July 22	.334	.333	.333	.387	.280	.333	.346	.321	.333	.417	.250	.333	.358	.309	.333
July 23	.363	.304	.333	.374	.292	.334	.409	.257	.334	.385	.282	.333	.371	.296	.333
July 24	.356	.311	.333	.377	.290	.333	.395	.272	.333	.413	.254	.333	.366	.300	.334
July 25	.335	.331	.334	.371	.296	.333	.379	.287	.334	.382	.285	.333	.369	.297	.334
July 26	.341	.326	.333	.401	.266	.333	.390	.277	.333	.407	.260	.333	.356	.311	.333

Table 1.

Tabular Form of $F_A$

$F_A$	$h_1$			$h_2$
	Membership	Non-membership	Hesitant	Membership	Non-membership	Hesitant
$e_1$	0.2	0.7	0.1	0.4	0.5	0.1
$e_2$	0.1	0.6	0.3	0.3	0.5	0.2

Table 2.

Temperature.

Date	Maharashtra			Tamil Nadu			Delhi			Andhra Pradesh			Karnataka
	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg
July 20	31	28	29.5	33	26	29.5	32	26	29	33	24	28.5	29	26	27.5
July 21	30	27	28.5	33	28	30.5	32	24	28	34	24	29	31	27	29
July 22	28	28	28	34	28	31	27	25	26	35	25	30	30	26	28
July 23	31	27	29	34	28	31	34	25	29.5	31	24	27.5	32	27	29.5
July 24	28	26	27	34	28	31	35	27	31	34	24	29	32	27	29.5
July 25	29	26	27.5	35	27	31	35	26	30.5	30	23	26.5	33	27	30
July 26	27	27	27	35	26	30.5	36	28	32	32	24	28	31	28	29.5

Table 4.

Humidity.

Date	Maharashtra			Tamil Nadu			Delhi			Andhra Pradesh			Karnataka
	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg
July 20	85	77	81	89	65	77	90	72	81	96	60	78	98	86	92
July, 21	91	78	84.5	88	67	77.5	99	85	92	96	58	77	94	82	88
July, 22	89	89	89	87	63	75	99	92	95.5	90	54	72	95	82	88.5
July, 23	92	77	84.5	82	64	73	97	61	79	90	66	78	94	75	84.5
July, 24	94	82	88	82	63	72.5	96	66	81	91	56	73.5	94	77	85.5
July, 25	83	82	82.5	84	67	75.5	95	72	83.5	94	70	82	92	74	83
July, 26	91	87	89	86	57	71.5	90	64	77	94	60	77	94	82	88

Table 6.

Confirmed Cases(Active + Recovered + Deceased).

Date	Maharashtra			Tamil Nadu			Delhi			Andhra Pradesh			Karnataka
	Act.	Rec.	Dec.	Act.	Rec.	Dec.	Act.	Rec.	Dec.	Act.	Rec.	Dec.	Act.	Rec.	Dec.
July 20	131334	175029	12030	51351	121776	2551	15166	104918	3663	28800	24228	696	42213	23795	1403
July 21	132236	182217	12276	51347	126670	2626	15288	106118	3690	32336	25574	758	44137	25459	1464
July 22	136980	187769	12556	51765	131583	3144	14954	107650	3719	31763	32127	823	47066	27239	1519
July 23	140093	194253	12854	52939	136793	3232	14554	109065	3745	34272	37555	884	49928	29310	1616
July 24	143714	199967	13132	53132	143297	3320	13681	110931	3777	39990	39935	933	52788	31347	1726
July 25	145481	207194	13389	52273	151055	3409	12657	113068	3806	44431	43255	985	55385	33750	1798
July 26	148601	213238	13656	53703	156526	3494	11904	114875	3827	48956	46301	1041	58414	35838	1880

Table 7.

Confirmed Cases in converted form.

Date	Maharashtra			Tamil Nadu			Delhi			Andhra Pradesh			Karnataka
	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg	Max	Min	Avg
July 20	.412	.550	.038	.292	.693	.015	.123	.847	.030	.536	.451	.013	.626	.353	.021
July 21	.405	.558	.037	.284	.701	.015	.123	.848	.029	.551	.436	.013	.621	.358	.021
July 22	.406	.557	.037	.277	.706	.017	.118	.852	.030	.491	.496	.013	.621	.359	.020
July 23	.403	.560	.037	.274	.709	.017	.114	.856	.030	.471	.516	.013	.618	.362	.020
July 24	.403	.560	.037	.266	.717	.017	.106	.864	.030	.495	.494	.011	.615	.365	.020
July 25	.397	.566	.037	.253	.731	.016	.098	.873	.029	.501	.488	.011	.609	.371	.020
July 26	.396	.568	.036	.251	.732	.017	.091	.880	.029	.508	.481	.011	.608	.373	.019

Table 8.

Correlation in tabular form.

Climate Variable	Active Cases	Recovered Cases	Deceased
Temperature Maximum	−0.3758	0.2106	−0.6143
Temperature Average	−0.0534	0.0505	0.0909
Temperature Minimum	0.1784	−0.2032	0.6024
Humidity Maximum	−0.3163	0.1154	−0.6561
Humidity Average	−0.2402	0.1465	−0.0235
Humidity Minimum	0.3014	−0.1190	0.6537

Conclusion

The weather parameters are an important factor in determining the occurrence rate of Covid-19 in India. Our findings provide preliminary evidence that the Covid-19 pandemic may be partially suppressed with temperature and humidity increases in India. A few words about possible extensions of the preceding conclusions:

• •Fixed point method for correlation between the weather conditions and 2019-nCoV model of type SEIARM in USA via fuzzy sets.
• •Fixed point method for correlation between the weather conditions and 2019-nCoV model of type SCIRD in Brazil via fuzzy sets.
• •Fixed point method for correlation between the weather conditions and 2019-nCoV model of type SIDARTHE in India via fuzzy sets.

Data availability

No data were used to support this study.

Authors contributions

MJB, BH and PSK formulated the problem. BH and PSK developed the theory and performed the computations. BH, PSK and JJN drafted and aligned the manuscript sequentially, thereafter verified the analytical methods. The four authors read and approved the final manuscript.

Funding

The work of J.J. Nieto has been partially supported by the Agencia Estatal de Investigacion (AEI) of Spain, co-financed by the European Fund for Regional Development (FEDER) corresponding to the 2014–2020 multi year financial framework, project MTM2016-75140-P; Xunta de Galicia under grant ED431C 2019/02; and Instituto de Salud Carlos III, grant COV20/00617.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.