Fig. 4. Bioinspired cilia arrays with optimal metachronal waves propagating on curved surfaces.

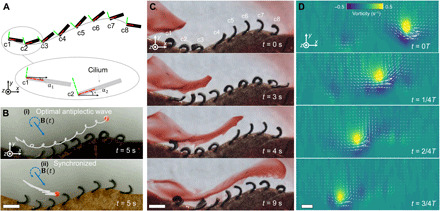
(A) Illustration of encoding metachronal waves in artificial cilia on curved surfaces. The key design rule is to compensate the rotation of the cilium-attached coordinate of each cilium by designing their magnetization phase profiles (see fig. S7). The red and green lines represent the +X and +Y axes of the cilium-attached coordinates, respectively. Cilia magnetization profiles: ${\mathrm{\varphi }}_i(s)=(i-1)\mathrm{\Delta }\mathrm{\varphi }-\frac{3\mathrm{\pi }}{8}+1.75\mathrm{\pi }\left(\frac{s}{L}\right)$, where Δϕ = −π/4. Boundary wall positions:$y_{\mathrm{ci}}=L\text{sin}\left(\frac{2{\mathrm{\pi }x}_{\mathrm{ci}}}{4L}\right)$, where x_ci (i = 1,2, …,8) is chosen with an equal spacing from −4L to 4L. (B) Comparison of the particle transportation performance between bioinspired cilia arrays with an (i) optimal metachronal wave (Δψ_s = −π/4) and (ii) synchronized motion (Δψ_s = 0). (C) Video snapshots of the fluid flow induced by an artificial cilia array (Δψ_s = −π/4) visualized by a food dye. Each column in an array has three identical cilia in the z direction. (D) Sequence of fluid flow vorticity and velocity distributions produced by the bioinspired cilia array with an optimal metachronal wave within a full period. Fluid flow data were measured using PIV. B(t): f = 2.5 Hz and B_m = 40 mT. Scale bars, 1 mm. Photo credit: Xiaoguang Dong, Max Planck Institute for Intelligent Systems.